Heat content asymptotics
Let $M$ be a compact Riemannian manifold with boundary $\partial M$. Assume given a decomposition of the boundary as the disjoint union of two closed sets $C _ { N }$ and $C _ { D }$. Impose Neumann boundary conditions on $C _ { N }$ and Dirichlet boundary conditions on $C _ { D }$. Let $u _ { \Phi }$ be the temperature distribution of the manifold corresponding to an initial temperature $\Phi$; $u _ { \Phi } ( x ; t )$ is the solution to the equations:
\begin{equation*} ( \partial _ { t } + \Delta ) u = 0, \end{equation*}
\begin{equation*} u ( x ; 0 ) = \Phi ( x ) , u _ { ; m } ( y ; t ) = 0 \text { for } y \in C _ { N } , t > 0, \end{equation*}
\begin{equation*} u ( y ; t ) = 0 \text { for } y \in C _ { D } , t > 0. \end{equation*}
Here, $u_{:m}$ denotes differentiation with respect to the inward unit normal. Let $\rho$ be a smooth function giving the specific heat. The total heat energy content of $M$ is given by
\begin{equation*} \beta ( \phi , \rho ) ( t ) = \int _ { M } u _ { \Phi } \rho. \end{equation*}
As $t \downarrow 0$, there is an asymptotic expansion
\begin{equation*} \beta ( \phi , \rho ) ( t ) \sim \sum _ { n \geq 0 } \beta _ { n } ( \phi , \rho ) t ^ { n / 2 }. \end{equation*}
The coefficients $\beta _ { n } ( \phi , \rho )$ are the heat content asymptotics and are locally computable.
These coefficients were first studied with $C _ { N }$ empty and with $\phi = \rho = 1$. Planar regions with smooth boundaries were studied in [a5], [a6], the upper hemisphere was studied in [a4], [a3], and polygonal domains in the plane were studied in [a7]. See [a11], [a12] for recursive formulas on a general Riemannian manifold.
More generally, let $L$ be the second fundamental form and let $R$ be the Riemann curvature tensor. Let indices $a$, $b$, $c$ range from $1$ to $m - 1$ and index an orthonormal frame for the tangent bundle of the boundary. Let ":" (respectively, ";" ) denote covariant differentiation with respect to the Levi-Civita connection of $\partial M$ (respectively, of $M$) summed over repeated indices. The first few coefficients have the form:
$\beta _ { 0 } ( \phi , \rho ) = \int _ { M } \phi \rho$;
$\beta _ { 1 } ( \phi , \rho ) = - 2 \pi ^ { - 1 / 2 } \int _ { C _ { D } } \phi \rho$;
 |
\begin{equation*} + \int _ { C _ { N } } \phi _ { ; m } \rho \,d y; \end{equation*}
 |
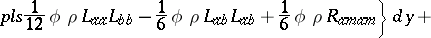 |
\begin{equation*} + \frac { 4 } { 3 } \pi ^ { - 1 / 2 } \int _ { C _ { N } } \phi _ { ; m } \rho _ { ; m } d y. \end{equation*}
The coefficient $\beta _ { 4 }$ is known.
The coefficients $\beta_5$ and $\beta_6$ have been determined if $C _ { D }$ is empty.
One can replace the Laplace operator $\Delta$ by an arbitrary operator of Laplace type as the evolution operator [a1], [a2], [a10], [a9]. One can study non-minimal operators as the evolution operator, inhomogeneous boundary conditions, and time-dependent evolution operators of Laplace type. A survey of the field is given in [a8].
References
| [a1] | M. van den Berg, S. Desjardins, P. Gilkey, "Functoriality and heat content asymptotics for operators of Laplace type" Topol. Methods Nonlinear Anal. , 2 (1993) pp. 147–162 |
| [a2] | M. van den Berg, P. Gilkey, "Heat content asymptotics of a Riemannian manifold with boundary" J. Funct. Anal. , 120 (1994) pp. 48–71 |
| [a3] | M. van den Berg, P. Gilkey, "Heat invariants for odd dimensional hemispheres" Proc. R. Soc. Edinburgh , 126A (1996) pp. 187–193 |
| [a4] | M. van den Berg, "Heat equation on a hemisphere" Proc. R. Soc. Edinburgh , 118A (1991) pp. 5–12 |
| [a5] | M. van den Berg, E.M. Davies, "Heat flow out of regions in ${\bf R} ^ { n }$" Math. Z. , 202 (1989) pp. 463–482 |
| [a6] | M. van den Berg, J.-F. Le Gall, "Mean curvature and the heat equation" Math. Z. , 215 (1994) pp. 437–464 |
| [a7] | M. van den Berg, S. Srisatkunarajah, "Heat flow and Brownian motion for a region in $\mathbf{R} ^ { 2 }$ with a polygonal boundary" Probab. Th. Rel. Fields , 86 (1990) pp. 41–52 |
| [a8] | P. Gilkey, "Heat content asymptotics" Booss (ed.) Wajciechowski (ed.) , Geometric Aspects of Partial Differential Equations , Contemp. Math. , 242 , Amer. Math. Soc. (1999) pp. 125–134 |
| [a9] | D.M. McAvity, "Surface energy from heat content asymptotics" J. Phys. A: Math. Gen. , 26 (1993) pp. 823–830 |
| [a10] | D.M. McAvity, "Heat kernel asymptotics for mixed boundary conditions" Class. Quant. Grav , 9 (1992) pp. 1983–1998 |
| [a11] | A. Savo, "Uniform estimates and the whole asymptotic series of the heat content on manifolds" Geom. Dedicata , 73 (1998) pp. 181–214 |
| [a12] | A. Savo, "Heat content and mean curvature" J. Rend. Mat. Appl. VII Ser. , 18 (1998) pp. 197–219 |
Heat content asymptotics. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Heat_content_asymptotics&oldid=50826