Hardy classes
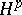 ,
, 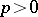
Classes of analytic functions 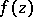 in the disc
in the disc 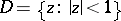 for which
for which
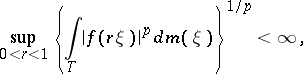 | (*) |
where 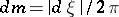 is the normalized Lebesgue measure on the circle
is the normalized Lebesgue measure on the circle 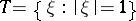 ; this is equivalent to the condition that the subharmonic function
; this is equivalent to the condition that the subharmonic function 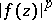 has a harmonic majorant in
has a harmonic majorant in 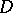 . Among the Hardy classes one also reckons the class
. Among the Hardy classes one also reckons the class  of bounded analytic functions in
of bounded analytic functions in 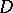 . The Hardy classes, which were introduced by F. Riesz in [1] and named by him in honour of G.H. Hardy, who first studied properties of
. The Hardy classes, which were introduced by F. Riesz in [1] and named by him in honour of G.H. Hardy, who first studied properties of 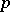 -means under the condition (*), play an important role in various problems of boundary properties of functions, in harmonic analysis, in the theory of power series, linear operators, random processes, and in the theory of extremal and approximation problems.
-means under the condition (*), play an important role in various problems of boundary properties of functions, in harmonic analysis, in the theory of power series, linear operators, random processes, and in the theory of extremal and approximation problems.
For any 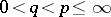 the inclusions
the inclusions 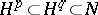 are strict, where
are strict, where 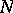 is the Nevanlinna class of functions of bounded characteristic (cf. Function of bounded characteristic); in particular, the functions of the Hardy classes have almost-everywhere on
is the Nevanlinna class of functions of bounded characteristic (cf. Function of bounded characteristic); in particular, the functions of the Hardy classes have almost-everywhere on 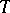 angular boundary values (cf. Angular boundary value)
angular boundary values (cf. Angular boundary value) 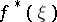 , from which the original functions
, from which the original functions 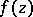 in
in 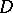 can be uniquely recovered. If
can be uniquely recovered. If 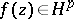 , then
, then 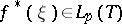 (the converse is not true for an arbitrary analytic function
(the converse is not true for an arbitrary analytic function 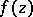 ), and
), and
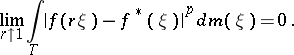 |
The classes 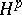 ,
, 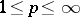 , are precisely the classes of analytic functions
, are precisely the classes of analytic functions 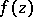 in
in 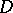 that have boundary values
that have boundary values 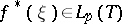 and that can be recovered from them by means of the Cauchy integral. But functions that can be represented in
and that can be recovered from them by means of the Cauchy integral. But functions that can be represented in 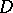 by an integral of Cauchy or Cauchy–Stieltjes type belong, generally speaking, only to the classes
by an integral of Cauchy or Cauchy–Stieltjes type belong, generally speaking, only to the classes 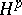 ,
, 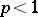 (the converse is not true). Univalent functions in
(the converse is not true). Univalent functions in 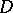 belong to all the classes
belong to all the classes 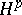 ,
, 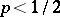 . The condition
. The condition 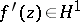 is necessary and sufficient for an analytic function
is necessary and sufficient for an analytic function 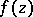 to be continuous in
to be continuous in 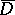 and absolutely continuous on
and absolutely continuous on 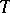 . If
. If 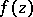 maps the disc
maps the disc 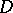 conformally onto a Jordan domain
conformally onto a Jordan domain 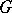 , then the condition
, then the condition 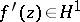 is equivalent to the contour
is equivalent to the contour 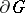 being rectifiable (see [2], [5]).
being rectifiable (see [2], [5]).
The existence of a one-to-one correspondence between the functions of Hardy classes and their boundary values makes it possible to regard, when this is convenient, functions 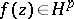 as functions on
as functions on 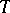 , and then the classes
, and then the classes 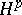 become closed subspaces of the Banach spaces
become closed subspaces of the Banach spaces 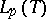 (these are complete linear metric spaces if
(these are complete linear metric spaces if 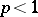 ). For
). For  these subspaces coincide with the closures in
these subspaces coincide with the closures in 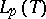 of the polynomials in
of the polynomials in 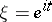 , and for
, and for 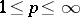 with the collections of those functions in
with the collections of those functions in  with vanishing Fourier coefficients of negative indices. The M. Riesz theorem asserts that the mapping
with vanishing Fourier coefficients of negative indices. The M. Riesz theorem asserts that the mapping 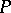 that can be expressed in terms of Fourier series by
that can be expressed in terms of Fourier series by
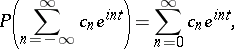 |
is a bounded projection of the Banach space 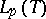 onto
onto 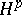 for every
for every 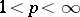 , but not for
, but not for  or
or 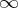 . This implies that the real spaces
. This implies that the real spaces 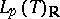 and
and 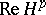 ,
, 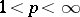 , are the same; for other values of
, are the same; for other values of 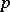 these spaces are essentially distinct, both in their approximation characteristics, in the structure of the dual spaces and (for
these spaces are essentially distinct, both in their approximation characteristics, in the structure of the dual spaces and (for 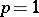 ) in relation to the properties of the Fourier coefficients (see [7], [9]).
) in relation to the properties of the Fourier coefficients (see [7], [9]).
The zero sets 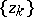 of non-trivial functions of the Hardy classes are completely characterized by the condition
of non-trivial functions of the Hardy classes are completely characterized by the condition 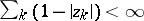 , which guarantees the uniform convergence on compacta inside
, which guarantees the uniform convergence on compacta inside 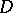 of a canonical Blaschke product
of a canonical Blaschke product
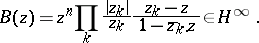 |
For every function 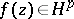 ,
,  ,
, 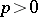 , there is an F. Riesz factorization
, there is an F. Riesz factorization 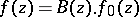 , where
, where 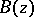 is the Blaschke product constructed from the zeros of
is the Blaschke product constructed from the zeros of 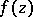 ,
, 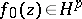 and
and 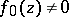 in
in 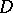 . The function
. The function 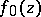 , in turn, decomposes into the product
, in turn, decomposes into the product 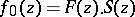 of the outer function
of the outer function
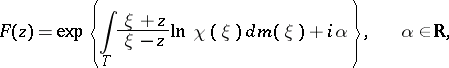 |
and the singular inner function
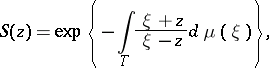 |
where 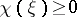 ,
,  and
and 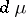 is a non-negative singular measure on
is a non-negative singular measure on 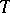 . The conditions
. The conditions
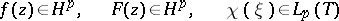 |
are equivalent, and 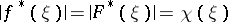 almost-everywhere on
almost-everywhere on 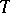 . Functions
. Functions  of the form
of the form 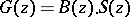 are called inner functions; they are completely characterized by the conditions
are called inner functions; they are completely characterized by the conditions 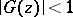 in
in  and
and 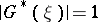 almost-everywhere on
almost-everywhere on 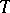 . Frequently one uses the decomposition
. Frequently one uses the decomposition  of an arbitrary function
of an arbitrary function  into the product of two functions in
into the product of two functions in 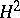 (see [4], [5]).
(see [4], [5]).
The class 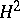 occupies a special place among the Hardy classes, since it is a Hilbert space with a reproducing kernel and has a simple description in terms of the Taylor coefficients:
occupies a special place among the Hardy classes, since it is a Hilbert space with a reproducing kernel and has a simple description in terms of the Taylor coefficients:
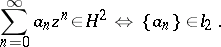 |
The study of the operator of multiplication by  , or the shift operator, in
, or the shift operator, in 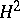 has played an important role; it turned out that all invariant subspaces of this operator are generated by inner functions
has played an important role; it turned out that all invariant subspaces of this operator are generated by inner functions 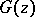 , that is, are of the form
, that is, are of the form 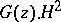 (see [4]).
(see [4]).
Under pointwise multiplication and the 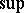 -norm the class
-norm the class 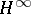 is a Banach algebra and the space of maximal ideals
is a Banach algebra and the space of maximal ideals 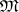 and the Shilov boundary have a very complicated structure (see [4]); the problem of the density of the ideals
and the Shilov boundary have a very complicated structure (see [4]); the problem of the density of the ideals 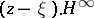 ,
, 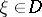 , in the space
, in the space  with the usual Gel'fand topology (the so-called Corona problem) was solved affirmatively on the basis of a description of the universal interpolation sequences, that is, sequences
with the usual Gel'fand topology (the so-called Corona problem) was solved affirmatively on the basis of a description of the universal interpolation sequences, that is, sequences 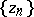 ,
, 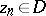 , such that
, such that 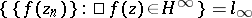 (see [5], [9]).
(see [5], [9]).
The Hardy classes 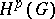 ,
, 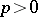 , of analytic functions
, of analytic functions 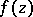 in domains
in domains 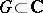 other than the disc can be defined (non-equivalently, in general) by starting out either from the condition that the functions
other than the disc can be defined (non-equivalently, in general) by starting out either from the condition that the functions 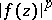 have harmonic majorants in
have harmonic majorants in 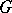 or from the condition of boundedness of the integrals
or from the condition of boundedness of the integrals 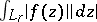 over families of contours
over families of contours 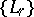 ,
, 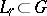 , that in a certain sense approximate the boundary of
, that in a certain sense approximate the boundary of 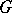 . The first method also makes it possible to define Hardy classes on Riemann surfaces. The second method leads to classes that are better adapted for the solution of extremal and approximation problems; in the case of Jordan domains
. The first method also makes it possible to define Hardy classes on Riemann surfaces. The second method leads to classes that are better adapted for the solution of extremal and approximation problems; in the case of Jordan domains 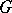 with a rectifiable boundary the latter classes are called Smirnov classes and are denoted by
with a rectifiable boundary the latter classes are called Smirnov classes and are denoted by 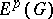 (see [2] and Smirnov class). For a half-plane, for example
(see [2] and Smirnov class). For a half-plane, for example 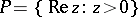 , the classes
, the classes 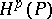 ,
, 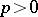 , defined by the condition
, defined by the condition
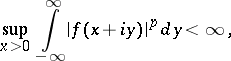 |
are closely related in their properties to the Hardy classes for the disc, however, their applications in harmonic analysis are connected not with the theory of Fourier series, but with Fourier transforms.
The Hardy classes of analytic functions 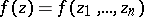 in the unit ball
in the unit ball 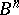 and the unit polydisc
and the unit polydisc 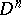 of the space
of the space 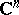 are defined by the condition (*), where the circle
are defined by the condition (*), where the circle 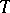 is replaced by the sphere
is replaced by the sphere 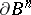 or the distinguished boundary
or the distinguished boundary 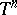 of the polydisc. The specific nature of the higher-dimensional case becomes manifest, first of all, in the absence of a simple characterization of the zero sets and of a factorization of functions in the Hardy classes (see [6], [10]). Hardy classes can also be defined in various ways for other domains in
of the polydisc. The specific nature of the higher-dimensional case becomes manifest, first of all, in the absence of a simple characterization of the zero sets and of a factorization of functions in the Hardy classes (see [6], [10]). Hardy classes can also be defined in various ways for other domains in 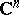 (see [10]).
(see [10]).
The higher-dimensional analogues of the Hardy classes (see [3]) are the so-called Hardy spaces, that is, spaces 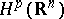 ,
, 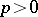 , of Riesz systems: real-valued vector functions
, of Riesz systems: real-valued vector functions 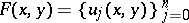 ,
,  ,
, 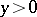 , satisfying the generalized Cauchy–Riemann conditions
, satisfying the generalized Cauchy–Riemann conditions
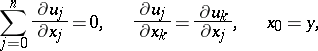 |
for which
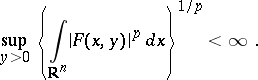 |
The definition of these spaces can also be given in terms of only the "real parts" 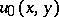 of the systems
of the systems 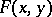 by requiring that the function
by requiring that the function 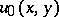 be harmonic and that its maximal function
be harmonic and that its maximal function
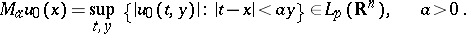 |
There are other characterizations of real-variable 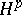 spaces.
spaces. 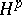 spaces can also be defined on homogeneous groups, i.e. Lie groups with underlying manifold
spaces can also be defined on homogeneous groups, i.e. Lie groups with underlying manifold 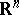 and dilations
and dilations 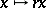 (see [11]).
(see [11]).
For 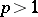 the transition from the function
the transition from the function 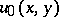 to its boundary values yields an identification of the spaces
to its boundary values yields an identification of the spaces 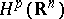 and
and 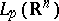 ; therefore, of interest is only the case
; therefore, of interest is only the case 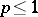 . It was just within the framework of the spaces
. It was just within the framework of the spaces 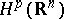 that fundamental results of the theory of Hardy classes such as the realization of the dual space
that fundamental results of the theory of Hardy classes such as the realization of the dual space 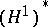 as the space of functions of bounded mean oscillation (see [8], [9]) and the atomic decomposition of the classes
as the space of functions of bounded mean oscillation (see [8], [9]) and the atomic decomposition of the classes 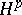 ,
, 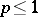 (see [7]), were first established. The characterization of Hardy classes in terms of the maximal function requires in a number of cases a recourse to probability concepts connected with Brownian motion (see [8]).
(see [7]), were first established. The characterization of Hardy classes in terms of the maximal function requires in a number of cases a recourse to probability concepts connected with Brownian motion (see [8]).
Abstract Hardy classes arise in the theory of uniform algebras (cf. Uniform algebra) and are not directly connected with analytic functions. Let a closed algebra 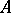 of continuous functions on a compact set
of continuous functions on a compact set 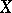 and a certain homomorphism
and a certain homomorphism 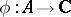 be fixed; there exists a positive measure
be fixed; there exists a positive measure 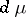 on
on 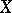 representing
representing 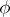 :
: 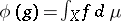 ,
, 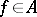 . By definition, the classes
. By definition, the classes 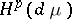 ,
, 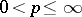 , are the closures (the weak closure for
, are the closures (the weak closure for 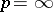 ) of the algebra
) of the algebra 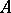 in the spaces
in the spaces 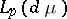 ; the study of the classes
; the study of the classes 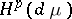 makes it possible to obtain additional information on
makes it possible to obtain additional information on 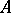 (see [12]).
(see [12]).
References
| [1] | F. Riesz, "Ueber die Randwerte einer analytischen Funktion" Math. Z. , 18 (1923) pp. 87–95 |
| [2] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [3] | E. Stein, G. Weiss, "On the theory of harmonic functions of several variables" Acta Math. , 103 (1960) pp. 25–62 |
| [4] | K. Hoffman, "Banach spaces of analytic functions" , Prentice-Hall (1962) |
| [5] | P.L. Duren, "Theory of 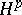 spaces" , Acad. Press (1970) spaces" , Acad. Press (1970) |
| [6] | W. Rudin, "Function theory in polydiscs" , Benjamin (1969) |
| [7] | R.R. Coifman, G. Weiss, "Extensions of Hardy spaces and their use in analysis" Bull. Amer. Math. Soc. , 83 : 4 (1977) pp. 569–645 |
| [8] | K.E. Petersen, "Brownian motion, Hardy spaces, and bounded mean oscillation" , Cambridge Univ. Press (1977) |
| [9] | P. Koosis, "Introduction to 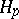 -spaces. With an appendix on Wolff's proof of the corona theorem" , Cambridge Univ. Press (1980) -spaces. With an appendix on Wolff's proof of the corona theorem" , Cambridge Univ. Press (1980) |
| [10] | W. Rudin, "Function theory in the unit ball in 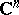 " , Springer (1980) " , Springer (1980) |
| [11] | G.B. Folland, E.M. Stein, "Hardy spaces on homogeneous groups" , Princeton Univ. Press (1982) |
| [12] | T.W. Gamelin, "Uniform algebras" , Prentice-Hall (1969) |
Comments
The result concerning the shift operator is commonly known as Beurling's theorem. The indicated solution of the corona problem in this article is due to L. Carleson. There is another, more recent, proof by T. Wolff based on the existence of good solutions of the inhomogeneous Cauchy–Riemann equations. The result about the dual of 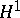 being BMO, the functions of bounded mean oscillation, is due to C. Fefferman. It is usually stated for
being BMO, the functions of bounded mean oscillation, is due to C. Fefferman. It is usually stated for 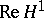 , because otherwise one has to introduce an unusual complex multiplication on real BMO, see [a1].
, because otherwise one has to introduce an unusual complex multiplication on real BMO, see [a1].
A measurable 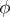 on
on 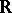 is called a BMO-function, or function of class BMO, if
is called a BMO-function, or function of class BMO, if 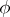 is locally integrable (i.e.
is locally integrable (i.e. 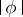 is integrable over any compact subset) and if, putting
is integrable over any compact subset) and if, putting
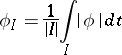 |
(the average of 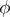 over the bounded interval
over the bounded interval 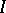 ), one has
), one has
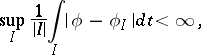 |
where the supremum is over all bounded intervals 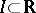 .
.
There are BMO-spaces on other domains, e.g. the unit circle 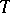 (
(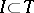 an arc, integration with respect to Lebesgue (or Haar) measure).
an arc, integration with respect to Lebesgue (or Haar) measure).
An important subclass is the class of VMO-functions, the class of functions of vanishing mean oscillation. Let 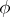 ,
, 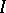 be as above. Write, for
be as above. Write, for 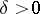 ,
,
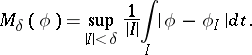 |
Then 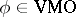 if
if  and
and 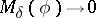 as
as 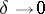 . (See [a1].)
. (See [a1].)
For 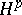 spaces of several variables see also [a2].
spaces of several variables see also [a2].
In addition to the numerous application areas already mentioned, the Hardy classes, especially 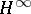 , are important in control theory, cf.
, are important in control theory, cf. 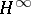 control theory.
control theory.
References
| [a1] | J.-B. Garnett, "Bounded analytic functions" , Acad. Press (1981) |
| [a2] | C. Fefferman, E.M. Stein, "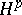 spaces of several variables" Acta Math. , 129 (1972) pp. 137–193 spaces of several variables" Acta Math. , 129 (1972) pp. 137–193 |
Hardy classes. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hardy_classes&oldid=35257