Handle theory
handle-body theory
One of the methods to study topological manifolds, based on the representation of a manifold as a union of topological balls with non-intersecting interiors and with boundaries intersecting in a special way.
Let $ M ^ {n} $ be an $ n $- dimensional manifold, $ k $ an integer such that $ 0 \leq k \leq n $, and let a topological ball $ H $ be the image of a homeomorphic mapping $ h : B ^ {k} \times B ^ {n-} k \rightarrow M ^ {n} $, where $ B ^ {m} $ denotes the standard $ m $- dimensional ball with centre at the point $ 0 $. Then the pair $ ( H , h ) $( or, simply, $ H $) is called a handle of index $ k $ in $ M ^ {n} $. The homeomorphism $ h $ is called the characteristic mapping of the handle $ H $, the disc $ h ( B ^ {k} \times 0 ) $ is called the core disc, and the disc $ h ( 0 \times B ^ {n-} k ) $ is called the transversal disc. The sphere $ h ( \partial B ^ {k} \times 0 ) $ is called the attaching (or base) sphere, and the sphere $ h ( 0 \times B ^ {n-} k ) $ is called the transversal sphere. The space $ h ( \partial B ^ {k} \times B ^ {n-} k ) $ is called the base of the handle $ H $.
If the manifold $ M ^ {n} $ is piecewise linear, then it makes sense to speak about piecewise-linear handles, meaning piecewise linearity of the characteristic mapping. Similarly, one can speak about smooth handles in the case when $ M ^ {n} $ is smooth.
Let $ ( H , h ) $ be a handle of index $ k $ in the manifold $ M ^ {n} $, let $ P $ be its base and let $ M _ {1} ^ {n} $ be a submanifold of $ M ^ {n} $ such that $ H \cap M _ {1} ^ {n} = P $. The transition from $ M _ {1} ^ {n} $ to $ M _ {2} ^ {n} = M _ {1} ^ {n} \cup H $ is called the operation of attaching a handle of index $ k $. The imbedding $ f = h \mid _ {\partial B \times B } $ is called the attaching mapping. Up to a homeomorphism invariant of $ M _ {1} ^ {n} $, the manifold $ M _ {2} ^ {n} $ is defined entirely by the attaching mapping $ f $ and is independent of the ambient manifold $ M ^ {n} $. If $ f $ is an arbitrary imbedding of $ \partial B ^ {k} \times B ^ {n-} k $ in $ \partial M _ {1} ^ {n} $, then the result of attaching a handle by means of $ f $ can be described as follows: $ M _ {2} ^ {n} = ( M _ {1} ^ {n} \cup ( B ^ {k} \times B ^ {n-} k ) ) / \sim $, where the equivalence relation $ \sim $ is generated by identification of the points of $ \partial B ^ {k} \times B ^ {n-} k $ and $ \partial M _ {1} ^ {n} $ by $ f $. The transition from $ \partial M _ {1} ^ {n} $ to $ \partial M _ {2} ^ {n} $ is called a spherical rearrangement (also called surgery). Manifolds obtained by attaching a handle by means of isotopic imbeddings are homeomorphic. In Fig. athe attaching of three-dimensional handles of indices 1 and 2 is shown. Attaching a handle of index 0 to $ M _ {1} ^ {n} $ consists of adding to $ M _ {1} ^ {n} $ a separately taken ball of dimension $ n $. Adding a handle of index $ n $ consists of pasting an $ n $- dimensional ball to one of the components of $ \partial M _ {1} ^ {n} $.
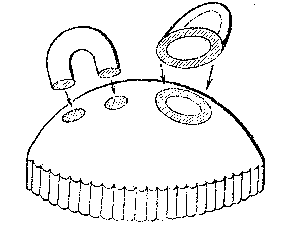
Figure: h046300a
If the manifold $ M _ {1} ^ {n} $ and the attaching imbedding $ f : \partial B ^ {k} \times B ^ {n-} k \rightarrow M _ {1} ^ {n} $ are piecewise linear, then the manifold $ M _ {2} ^ {n} $ obtained by attaching a handle by means of $ f $ is also piecewise linear. In the case of smooth $ M _ {1} ^ {n} $ and $ f $ the manifold $ M _ {2} ^ {n} $ has a natural smooth structure at all points except at "corner" points, the union of which coincides with the boundary of the handle's base. This structure can be uniquely extended to a smooth structure on the entire $ M _ {2} ^ {n} $. Such extension is called smoothing of corners. In the smooth case, smoothing of corners is included in attaching a handle. Attaching a smooth handle is completely defined by the attaching sphere with a trivialization of its normal bundle.
The representation of a compact manifold $ M ^ {n} $ as the union of a finite ordered family of handles in $ M ^ {n} $ is called a handle decomposition of $ M ^ {n} $ if each subsequent handle intersects the union of the preceding ones exactly along its base. In other words, $ M ^ {n} $ admits a handle decomposition if it can be obtained from a ball (or empty set) by sequentially attaching handles. Similarly, by a decomposition of a pair $ ( M ^ {n} , M _ {0} ^ {n} ) $, where $ M _ {0} ^ {n} $ is a submanifold of $ M ^ {n} $, one understands a representation of $ M ^ {n} $ as a result of sequentially attaching handles to $ M _ {0} ^ {n} $. In particular, a decomposition of a pair $ ( W , M _ {0} \times I ) $, where $ M _ {0} \times I $ is a collar of $ M _ {0} $, is called a handle decomposition of the bordism $ ( W , M _ {0} , M _ {1} ) $. A handle decomposition of a non-compact manifold $ M ^ {n} $ consists of an infinite number of handles. Here it is usually required that the decomposition be locally finite, i.e. each compact set in $ M ^ {n} $ intersects only a finite number of handles.
By transforming the transversal spheres of the already attached handles and the base sphere of the handle being attached into general position and by replacing the attaching mappings by isotopic ones (cf. Isotopy (in topology)), one may achieve that handles of the same index do not intersect and that the indices of sequentially attached handles do not decrease. Such a handle decomposition is called regular.
Each piecewise-linear manifold can be decomposed into piecewise-linear handles. If $ T $ is a triangulation of $ M ^ {n} $ and $ T ^ {\prime\prime} $ is its second barycentric subdivision, then as handles of index $ k $ one can take the closed stars in $ T ^ {\prime\prime} $ of the barycentres of $ k $- dimensional simplices of $ T $( see Fig. b; the definition of a star is given in Complex).
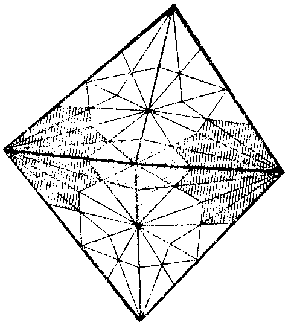
Figure: h046300b
There exists a close relation between smooth handle decompositions of a smooth manifold $ M ^ {n} $ and smooth functions on $ M ^ {n} $ with non-degenerate critical points — Morse functions (cf. Morse function). This relation is as follows. Let $ x _ {0} $ be a critical point of index $ k $ of a Morse function $ f : M ^ {n} \rightarrow \mathbf R $ such that for some $ \epsilon > 0 $ the inverse image of the interval $ [ f ( x _ {0} ) - \epsilon , f ( x _ {0} ) + \epsilon ] $ contains no other critical points, and let $ M _ {c} = \{ {x \in M ^ {n} } : {f ( x) \leq c } \} $. Then the manifold $ M _ {f ( x _ {0} ) + \epsilon } $ is obtained from the manifold $ M _ {f ( x _ {0} ) - \epsilon } $ by means of attaching a smooth handle of index $ k $. Thus, each Morse function on a compact manifold $ M ^ {n} $ generates a smooth handle decomposition of $ M ^ {n} $; moreover, the number of handles of index $ k $ in this decomposition coincides with the number of critical points of index $ k $. This proves the existence of a smooth handle decomposition for any smooth manifold. Conversely, each smooth handle decomposition of $ M ^ {n} $ is generated by some Morse function on $ M ^ {n} $.
The problem of decomposition of topological manifolds into handles is more complicated. It is known that any closed topological manifold of dimension $ n \geq 5 $ can be decomposed into topological handles. Manifolds of dimension $ n \leq 3 $ are combinatorially triangulable and, thus, can be decomposed into handles. It has been proved that there exists a manifold of dimension 4 which does not admit a handle decomposition.
If in the regular handle decomposition of a manifold $ M ^ {n} $ one contracts sequentially all handles to their core disc, then one obtains a cellular space $ K $. To each handle of index $ k $ in the decomposition of $ M ^ {n} $ then corresponds a $ k $- dimensional cell in the CW-complex of $ K $. The space $ K $ is of the same homotopy type as $ M ^ {n} $. If $ M ^ {n} $ is closed, $ K $ coincides with $ M ^ {n} $.
From the definition of a handle it follows that each $ n $- dimensional handle $ H $ of index $ k $ is at the same time a handle of index $ n - k $. If $ P _ {k} $ is the base of $ H $ as a handle of index $ k $ and $ P _ {n-} k $ is the base of $ H $ as a handle of index $ n - k $, then $ P _ {k} \cup P _ {n-} k = \partial H $ and $ P _ {k} \cap P _ {n-} k = \partial P _ {k} = \partial P _ {n-} k $. Each handle decomposition of a closed manifold $ M ^ {n} $ generates a so-called dual handle decomposition of $ M ^ {n} $. The dual decomposition consists of the handles of the initial decomposition taken in reverse order, moreover, each handle of index $ k $ is considered already as a handle of index $ n - k $. This fact is the geometric foundation for Poincaré duality. If the manifold $ M ^ {n} $ has a boundary, then the dual decomposition can be considered as a decomposition of the pair $ ( M ^ {n} \cup ( \partial M ^ {n} \times I ) , \partial M ^ {n} \times I ) $.
Let $ H _ {1} , H _ {2} $ be non-intersecting handles of index $ k $ attached to a manifold $ M ^ {n} $ with a simply-connected boundary by imbeddings $ f _ {1} , f _ {2} : \partial B ^ {k} \times B ^ {n-} k \rightarrow \partial M ^ {n} $. Let $ k \geq 2 $ and $ n - k \geq 2 $ and let $ [ f] $ denote the element of the group $ \pi _ {k-} 1 (\partial M ^ {n} ) $ determined by $ f $. Then the imbedding $ f _ {2} $ is isotopic in $ \partial ( M ^ {n} \cup H _ {1} ) $ to an imbedding $ f _ {2} ^ { \prime } : \partial B ^ {k} \times B ^ {n-} k \rightarrow \partial M ^ {n} $ such that $ [ f _ {2} ^ { \prime } ] = [ f _ {1} ] + [ f _ {2} ] $. This means that the manifolds $ M ^ {n} \cup H _ {1} \cup H _ {2} $ and $ M ^ {n} \cup H _ {1} \cup H _ {2} ^ \prime $, where $ H _ {2} ^ \prime $ is the handle attached by means of $ f _ {2} ^ { \prime } $, are homeomorphic. The transition from the manifold $ M ^ {n} \cup H _ {1} \cup H _ {2} $ to the manifold $ M ^ {n} \cup H _ {1} \cup H _ {2} ^ \prime $ is called addition of handles.
Let a manifold $ M _ {2} ^ {n} $ be obtained from a manifold $ M _ {1} ^ {n} $ by subsequently attaching a handle $ H _ {1} $ of index $ k $ and a handle $ H _ {2} $ of index $ k + 1 $ so that the base sphere of $ H _ {2} $ cuts transversally the transversal sphere of $ H _ {1} $ in exactly one point. Then this pair of handles can be removed. This means that there exists a homeomorphism of $ M _ {2} ^ {n} $ onto $ M _ {1} ^ {n} $ which is the identity outside a neighbourhood of $ H _ {1} \cup H _ {2} $. This operation of removing is sometimes called cancellation of additional handles. Addition of handles and cancellation of handles can be carried out while staying within the piecewise-linear or the smooth category. By cancellation of the handles of indices 0 and 1 one can, for example, replace any handle decomposition of a compact connected manifold $ M ^ {n} $ by the handle decomposition with exactly one handle of index 0. If $ M ^ {n} $ is simply connected and $ n \geq 5 $, then by addition and cancellation of handles one can reduce any handle decomposition to a decomposition with a minimal number of handles compatible with the homological structure of $ M ^ {n} $.
Let $ ( H , h ) $ be a topological handle of index $ k $ in a piecewise-linear manifold $ M ^ {n} $; moreover, let the characteristic mapping $ h $ be piecewise linear in a neighbourhood of $ \partial B ^ {k} \times B ^ {n-} k $. Is there an isotopy of $ h $ that is the identity in a neighbourhood of $ \partial B ^ {k} \times B ^ {n-} k $ and which straightens the handle $ H $, i.e. transforms it into a piecewise-linear handle? If the answer to this question is always positive, then on each topological manifold one can introduce a piecewise-linear structure by making the structures on the coordinate neighbourhood compatible using straightening piecewise-linear handles of one neighbourhood inside another. In reality the answer depends on the index $ k $ and the dimension $ n $ of the handle $ H $. If $ n \leq 3 $ or $ n \geq 5 $ and $ k \neq 3 $, then any handle can be straightened. It is known that when $ n \geq 5 $ there exists handles of index 3 that cannot be straightened; moreover, the obstruction to straightening lies in the group $ \mathbf Z _ {2} $. In dimension 4, the handles of indices 0 and 1 can be straightened, and those of indices 2 and 3, in general, can not. It are the so-called Milnor groups $ \Gamma _ {k} $ that form obstructions to smoothing piecewise-linear handles.
References
| [1] | S. Smale, "Generalised Poincaré conjecture in dimensions $>4$" Ann. of Math (2) , 74 (1961) pp. 391–466 |
| [2] | S. Smale, "Structure of manifolds" Amer. J. Math. , 84 (1962) pp. 387–399 |
| [3] | S. Smale, "A survey of some recent developments in differential topology" Bull. Amer. Math. Soc. , 69 (1963) pp. 131–145 |
| [4] | R.C. Kirby, L.C. Siebenmann, "Foundational essays on topological manifolds, smoothings, and triangulations" , Princeton Univ. Press (1977) |
| [5] | C.P. Rourke, B.J. Sanderson, "Introduction to piecewise-linear topology" , Springer (1972) |
| [6] | V.A. Rokhlin, D.B. Fuks, "Beginner's course in topology. Geometric chapters" , Springer (1984) (Translated from Russian) |
| [a1] | J.W. Milnor, "Morse theory" , Princeton Univ. Press (1963) |
| [a2] | J. Milnor, "Lectures on the $h$-cobordism theorem" , Princeton Univ. Press (1965) |
Handle theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Handle_theory&oldid=54248