H^infinity-control-theory
A branch of control theory where the performance of a dynamical system (cf. Automatic control theory) is appraised in terms of the $ H ^ \infty $-
norm. The Banach space $ H ^ \infty $(
named after G.H. Hardy, cf. Hardy classes) consists of all complex-valued functions of a complex variable which are analytic and of bounded modulus in the open right half-plane. The norm of such a function is the supremum modulus:
$$ \| F \| _ \infty = \sup _ { \mathop{\rm Re} s > 0 } | F( s) | . $$
By a theorem of Fatou (cf. Fatou theorem), such a function has a boundary value $ F( i \omega ) $ for almost-all $ \omega $, and, moreover,
$$ \| F \| _ \infty = \mathop{\rm esssup} _ \omega | F( i \omega ) | . $$
The theory of $ H ^ \infty $ control was initiated by G. Zames [a1], [a2], [a3], who formulated a basic feedback problem as an optimization problem with an operator norm, in particular, an $ H ^ \infty $- norm. Relevant contemporaneous works are those of J.W. Helton [a4] and A. Tannenbaum [a5].
The theory treats dynamical systems represented as integral operators of the form
$$ y( t) = \int\limits _ { 0 } ^ { t } g( t- \tau ) x( \tau ) d \tau . $$
Here $ g $ is sufficiently regular to make the input-output mapping $ x \mapsto y $ a bounded operator on $ L _ {2} [ 0 , \infty ) $. Taking Laplace transforms gives $ Y( s)= G( s) X( s) $. The function $ G $ is called the transfer function of the system and it belongs to $ H ^ \infty $ because the integral operator is bounded. Moreover, the $ H ^ \infty $- norm of $ G $ equals the norm of the integral operator, i.e.,
$$ \tag{a1 } \| G \| _ \infty = \sup _ {\| x \| _ {2} \leq 1 } \ \| y \| _ {2} . $$
There are two prototype problems giving rise to an optimality criterion with the $ H ^ \infty $- norm. The first is the problem of robust stability of the feedback system
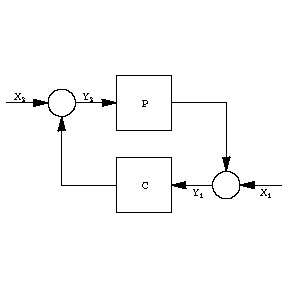
Figure: h046020a
Here $ P $ and $ C $ are transfer functions in $ H ^ \infty $, and $ X _ {1} $, $ X _ {2} $, $ Y _ {1} $, $ Y _ {2} $ are Laplace transforms of signals; $ P $ represents a "plant" , the dynamical system which is to be controlled, and $ C $ represents the "controller" (cf. also Automatic control theory). The figure stands for the two equations
$$ Y _ {1} = X _ {1} + PY _ {2} ,\ Y _ {2} = X _ {2} + CY _ {1} , $$
which can be solved to give
$$ \left [ \begin{array}{c} Y _ {1} \\ Y _ {2} \end{array} \right ] = \ \left [ \begin{array}{cc} \frac{1 }{1- PC } & \frac{P }{1- PC } \\ \frac{C }{1- PC } & \frac{1 }{1- PC } \\ \end{array} \right ] \left [ \begin{array}{c} X _ {1} \\ X _ {2} \end{array} \right ] . $$
Therefore, the input-output mapping for the feedback system has four transfer functions. The feedback system is said to be internally stable if these four transfer functions are all in $ H ^ \infty $. A simple sufficient condition for this is $ \| PC \| _ \infty < 1 $.
Internal stability is robust if it is preserved under perturbation of $ P $. There are several possible notions of perturbation, typical of which is additive perturbation. So suppose $ P $ is perturbed to $ P+ \Delta P $, with $ \Delta P $ in $ H ^ \infty $. About $ \Delta P $ it is assumed that only a bound on $ | \Delta P( i \omega ) | $ is known, namely,
$$ | \Delta P( i \omega ) | < | R( i \omega ) | ,\ \textrm{ a.a. } \ \omega , $$
where $ R \in H ^ \infty $. J.C. Doyle and G. Stein [a6] showed that internal stability is preserved under all such perturbations if and only if
$$ \tag{a2 } \| RC( 1- PC) ^ {- 1 } \| _ \infty < 1 . $$
This leads to the robust stability design problem: Given $ P $ and $ R $, find $ C $ so that the feedback system is internally stable and (a2) holds.
The second problem relates to the same feedback system. Suppose $ X _ {2} = 0 $, $ X _ {1} $ represents a disturbance signal, and the objective is to reduce the effect of $ X _ {1} $ on the output $ Y _ {1} $. The transfer function from $ X _ {1} $ to $ Y _ {1} $ equals $ ( 1- PC) ^ {- 1 } $. Suppose, in addition, that the disturbance is not a fixed signal, but can be the output of another system with any input in $ L _ {2} [ 0 , \infty ) $ of unit norm; let this latter system have transfer function $ W $ in $ H ^ \infty $. Then, in view of (a1), the supremal $ L _ {2} [ 0 , \infty ) $- norm of $ y _ {1} $ over all such disturbances equals $ \| W( 1- PC) ^ {- 1 } \| _ \infty $. This leads to the disturbance attenuation problem: Given $ P $ and $ R $, find $ C $ to achieve internal stability and minimize $ \| W( 1- PC) ^ {- 1 } \| _ \infty $.
The above two problems are special cases of the more general standard $ H ^ \infty $ control problem. It can be solved by reduction to the Nehari problem of approximating a function in $ L _ \infty $( bounded functions on the imaginary axis) by one in $ H ^ \infty $. A summary of this theory is in [a7], and a detailed treatment is in [a8].
References
| [a1] | G. Zames, "Feedback and complexity, Special plenary lecture addendum" , IEEE Conf. Decision Control , IEEE (1976) |
| [a2] | G. Zames, "Optimal sensitivity and feedback: weighted seminorms, approximate inverses, and plant invariant schemes" , Proc. Allerton Conf. , IEEE (1979) |
| [a3] | G. Zames, "Feedback and optimal sensitivity: model reference transformations, multiplicative seminorms, and approximate inverses" IEEE Trans. Auto. Control , AC-26 (1981) pp. 301–320 |
| [a4] | J.W. Helton, "Operator theory and broadband matching" , Proc. Allerton Conf. , IEEE (1979) |
| [a5] | A. Tannenbaum, "On the blending problem and parameter uncertainty in control theory" Techn. Report Dept. Math. Weizmann Institute (1977) |
| [a6] | J.C. Doyle, G. Stein, "Multivariable feedback design: concepts for a classical modern synthesis" IEEE Trans. Auto. Control , AC-26 (1981) pp. 4–16 |
| [a7] | B.A. Francis, J.C. Doyle, "Linear control theory with an $H ^ { \infty }$ optimality criterion" SIAM J. Control and Opt. , 25 (1987) pp. 815–844 |
| [a8] | B.A. Francis, "A course in $H _ { \infty }$ control theory" , Lect. notes in control and inform. science , 88 , Springer (1987) |
H^infinity-control-theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=H%5Einfinity-control-theory&oldid=55351