Graph isomorphism
An equivalence relation on the set of graphs. An isomorphic mapping of a non-oriented graph to another one is a one-to-one mapping of the vertices and the edges of one graph onto the vertices and the edges, respectively, of the other, the incidence relation being preserved. Two graphs are said to be isomorphic if there exists an isomorphic mapping of one of these graphs to the other. In the figure, the graphs $G_1$ and $G_2$ are not isomorphic, whereas the graphs $G_1$ and $G_3$ are isomorphic. Isomorphic graphs are usually not distinguished from one another. The number of pairwise non-isomorphic graphs with a given number of vertices and a given number of edges is finite. Isomorphism of oriented graphs, hypergraphs and networks can be defined in a similar manner.
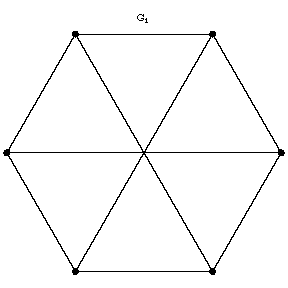
Figure: g044950a
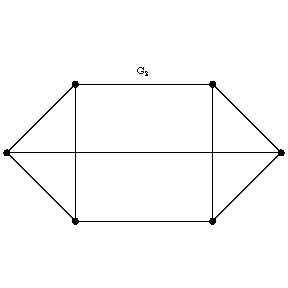
Figure: g044950b
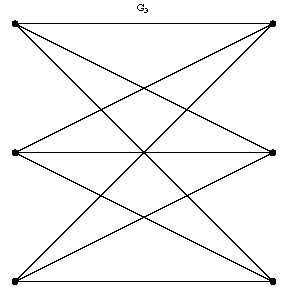
Figure: g044950c
The problem of establishing an isomorphism between graphs is an important problem in graph theory. There are algorithms for certain classes of graphs with the aid of which isomorphism can be fairly effectively recognized (e.g. for trees, cf. Tree, or planar graphs, [1]). Certain classes of graphs with $n$ vertices have been proved to be uniquely reconstructible (up to an isomorphism) from the set of subgraphs $G-v$ of it with $n-1$ vertices obtained by removing the vertex $v$ in all possible ways. This has been established, in particular, for trees and tournaments (for $n \neq 5,6$, cf. Tournament)
References
| [1] | J.E. Hopcroft, R.E. Tarjan, "Isomorphism of planar graphs" R.E. Miller (ed.) J.W. Tatcher (ed.) , Complexity of Computer Computations. Proc. Symp. IBM , Plenum (1972) pp. 131–152; 187–212 |
| [2] | P.J. Kelly, "A congruence theorem for trees" Pacific J. Math. , 7 (1957) pp. 961–968 |
Comments
The graph isomorphism problem in general belongs to the class $\mathcal{N}$ but has not been proved to be in the class $\mathcal{NPC}$ or $\mathcal{P}$ and is of great interest in the study of computational complexity. See the surveys [a1] and [a2] and also Complexity theory.
The reconstruction problem is usually called the Kelly–Ulam reconstruction conjecture. The earliest reference is in [a3]. Many classes of graphs have since been proved to be reconstructible. For recent surveys see [a4] and [a5].
References
| [a1] | R.C. Read, D.G. Corneil, "The graph isomorphism disease" J. Graph Theory , 1 (1977) pp. 339–363 |
| [a2] | G. Gati, "Further annotated bibliography on the isomorphism disease" J. Graph Theory , 3 (1979) pp. 95–109 |
| [a3] | S.M. Ulam, "A collection of mathematical problems" , Wiley (1960) |
| [a4] | J.A. Bondy, R.L. Hemminger, "Graph reconstruction—a survey" J. Graph Theory , 1 (1977) pp. 227–268 |
| [a5] | C.St.J.A. Nash-Williams, "The reconstruction problem" L.W. Beineke (ed.) R.J. Wilson (ed.) , Selected Topics in Graph Theory , Acad. Press (1978) pp. Chapt. 8 |
| [a6] | J.E. Hopcroft, R.E. Tarjan, "Isomorphism of planar graphs" R.E. Miller (ed.) J.W. Tatcher (ed.) , Complexity of Computer Computations. Proc. Symp. IBM , Plenum (1972) pp. 131–152; 187–212 |
| [a7] | J.E. Hopcroft, R.E. Tarjan, "Efficient planarity testing" J. ACM , 21 (1974) pp. 549–568 |
Graph isomorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Graph_isomorphism&oldid=33821