Graph, planar

A graph that can be regularly imbedded in the plane (cf. Graph imbedding). In other words, a graph $G$ is said to be planar if it can be represented in the plane so that various points of the plane correspond to its vertices and so that the lines corresponding to the edges of the graph do not pass through the points which correspond to the vertices (except for their terminal points) and do not mutually intersect. Problems such as the problem of colouring maps, the problem of design of communications, problems in radio-electronics which involve the realization of a circuit with the aid of planar printed subcircuits, etc., can be reduced to the study of planar graphs. Any regular (with non-intersecting edges) imbedding of a connected planar graph involves a subdivision of the plane into individual domains (faces). Such a subdivision of the plane is known as a planar map. Euler's formula

$$n-m+r=2,$$

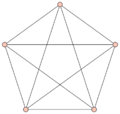
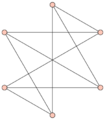
where $n$ is the number of vertices, $m$ is the number of edges and $r$ is the number of faces of the map (including the exterior face) applies to any planar map. It follows that the graph $K_5$ (the complete graph with $n=5$) and $K_{3,3}$ (the complete bipartite graph) which has three vertices in each of its parts, are not planar (Fig. a).

• 

  $K_5$

• 

  $K_{3,3}$

In a certain sense, these graphs are minimal non-planar graphs, according to the Pontryagin–Kuratowski theorem: A graph is planar if and only if it does not contain a subgraph homeomorphic to the graph $K_5$ or $K_{3,3}$ (cf. Graph homeomorphism).

There also exist other criteria of planarity (i.e. of whether or not a graph is planar). In particular, a graph $G$ is planar if and only if each of its non-trivial doubly-connected components has a cycle basis $Z_1,\ldots,Z_m$ and an additional cycle $Z_0$ such that any edge of $G$ is part of precisely two out of these $m+1$ cycles (a cycle basis is a subset of cycles of a given graph which is independent and complete in the set of all cycles of the graph with respect to the operation of addition modulo 2, cf. Graph).

Any planar graph can be represented in the plane so that all its edges are segments of a straight line. Any triply-connected graph (cf. Graph, connectivity of a) can be uniquely imbedded in the sphere (up to a homeomorphism of the sphere). Each imbedding of a planar graph in the plane, and hence each planar map, can be brought into one-to-one correspondence with its geometric dual graph, which is obtained as follows. A vertex of the planar graph is introduced into each face of the map and, if two faces have a common edge $e$, the vertices they contain are joined by the edge $e^*$ which intersects $e$ only once (in Fig. bthe imbedding of the graph is represented by continuous lines, while the dotted lines represent its dual graph).

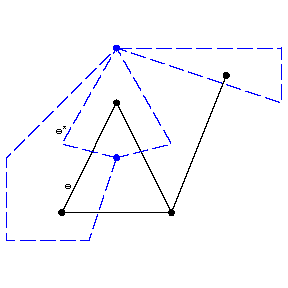
Figure: g044990b

A planar map each side of which is bounded by three edges is said to be a planar triangulation. The number of edges of a planar triangulation with $n$ vertices is $3n-6$.

An intensively studied subject in the theory of graphs is the colouring of planar graphs (cf. Graph colouring); for non-planar graphs one studies various numerical characteristics yielding the degree of non-planarity, including the genus, the thickness or coarseness of the graph, the number of crossings, etc. (cf. Graph imbedding).

References

[1]	F. Harary, "Graph theory" , Addison-Wesley (1969) pp. Chapt. 9

Comments

A comprehensive account of planar graphs and the celebrated four-colour conjecture that every planar graph is $4$-vertex-colourable is given by O. Ore in [a1]. Recently this conjecture was proved by K. Appel and W. Haken, see Four-colour problem. For a good summary of their work see also [a2].

References

[a1]	O. Ore, "The four-colour problem" , Acad. Press (1967)
[a2]	D.R. Woodall, R.J. Wilson, "The Appel–Haken proof of the four-colour theorem" L.W. Beineke (ed.) R.J. Wilson (ed.) , Selected Topics in Graph Theory , Acad. Press (1978) pp. Chapt. 4
[a3]	R.J. Wilson, "Introduction to graph theory" , Longman (1985)