Goniometry
The part of trigonometry determined by trigonometric functions and their relations.
Comments
Goniometry is the part of mathematics in which the so-called goniometric functions are studied, of which the most important are: sine, cosine and tangent. These functions can be defined in a purely geometric way as follows
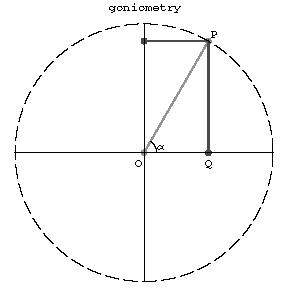
Figure: g044590a
$$\sin\alpha=\frac{PQ}{OP},\quad\cos\alpha=\frac{OQ}{OP},\quad\tan\alpha=\frac{PQ}{OQ}.$$
It can be shown that for arbitrary real $x$ the following series expansions hold:
$$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dotsb,$$
$$\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\dotsb.$$
As these series are convergent for arbitrary complex numbers too, the said functions can be extended to the whole complex plane and be studied for their own sake without any geometric application.
Important parts of goniometry are plane and spherical trigonometry. In plane trigonometry the main problem is to compute three of the six elements of a plane triangle (3 sides and 3 angles) if three of them are known. The object of spherical trigonometry is to study the properties of spherical triangles. Applications of these disciplines can be found in surveying and navigation.
See also Inverse trigonometric functions.
Goniometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Goniometry&oldid=44667