Gauss-Manin connection
The Gauss–Manin connection is a way to differentiate cohomology classes with respect to parameters. Consider a smooth projective curve $ X $
over a field $ K $.
Its first de Rham cohomology group $ H _ { \mathop{\rm dR} } ^ {1} ( X/K) $
can be identified with the space of differentials of second kind on $ X $
modulo exact differentials (cf. Differential). Each derivation $ \theta $
of $ K $(
cf. Derivation in a ring) can be lifted in a canonical way to a mapping $ \nabla _ \theta : H _ { \mathop{\rm dR} } ^ {1} ( X/K) \rightarrow H _ { \mathop{\rm dR} } ^ {1} ( X/K) $
satisfying $ \nabla _ \theta ( g \omega ) = g \nabla _ \theta ( \omega ) + \theta ( g) \omega $
for $ g \in K $,
$ \omega \in H _ { \mathop{\rm dR} } ^ {1} ( X/K) $[a1], [a2]. This amounts to a connection
$$ \nabla : \ H _ { \mathop{\rm dR} } ^ {1} ( X/K) \rightarrow \ \Omega _ {K} ^ {1} \otimes H _ { \mathop{\rm dR} } ^ {1} ( X/K) $$
which is integrable (i.e. $ \nabla _ {[ \theta , \theta ^ \prime ] } = [ \nabla _ \theta , \nabla _ {\theta ^ \prime } ] $). If $ K $ is a function field in one variable, one obtains the Picard–Fuchs equation $ \nabla \omega = 0 $, which has regular singular points (cf. Regular singular point).
The generalization to higher dimension is due to A. Grothendieck [a3]. For a proper and smooth morphism $ f: X \rightarrow S $ of $ \mathbf C $- schemes the de Rham cohomology of the fibres of $ f $ is described by the locally free $ {\mathcal O} _ {S} $- modules $ H _ { \mathop{\rm dR} } ^ {n} ( X/S) = R ^ {n} f _ \star ( \Omega _ {X/S} ^ {\bullet } ) $, the relative de Rham cohomology sheaves. From now on suppose that $ S $ is of finite type over $ \mathbf C $ and let $ X ^ {h} $ and $ S ^ {h} $ denote the underlying analytic spaces. Then
$$ H _ { \mathop{\rm dR} } ^ {n} ( {X ^ {h} } / {S ^ {h} } ) \cong \ {\mathcal O} _ {S ^ {h} } \otimes _ {\mathbf C} R ^ {n} f _ \star \mathbf C _ {X ^ {h} } , $$
and the analytic version of the Gauss–Manin connection is defined by $ \nabla ( g \omega ) = dg \otimes \omega $ for $ g $( respectively, $ \omega $) a local section of $ {\mathcal O} _ {S ^ {h} } $( respectively, $ R ^ {n} f _ \star \mathbf C _ {X ^ {h} } $).
An algebraic construction has been given by N.M. Katz and T. Oda [a4]. The complex $ \Omega _ {X/ \mathbf C } ^ {\bullet } $ is filtered by subcomplexes $ \phi ^ {i} $, where
$$ \phi ^ {i} \Omega _ {X/ \mathbf C } ^ {p} = \ \textrm{ image } \textrm{ of } \ ( f ^ { \star } \Omega _ {S/ \mathbf C } ^ {i} \otimes \Omega _ {X/ \mathbf C } ^ {p - i } \rightarrow \ \Omega _ {X/ \mathbf C } ^ {p} ). $$
One has $ ( \phi ^ {i} / \phi ^ {i + 1 } ) ^ {n} \cong f ^ { \star } \Omega _ {S/ \mathbf C } ^ {i} \otimes \Omega _ {X/S} ^ {n - i } $ and $ R ^ {n} f _ \star ( \phi ^ {i} / \phi ^ {i + 1 } ) \cong \Omega _ {S/ \mathbf C } ^ {i} \otimes H _ { \mathop{\rm dR} } ^ {n - i } ( X/S) $. The connecting homomorphism $ \nabla : R ^ {n} f _ \star ( \phi ^ {0} / \phi ^ {1} ) \rightarrow R ^ {n + 1 } f _ \star ( \phi ^ {1} / \phi ^ {2} ) $ in the long exact hypercohomology sequence associated to the exact sequence
$$ 0 \rightarrow \ \phi ^ {1} / \phi ^ {2} \rightarrow \ \phi ^ {0} / \phi ^ {2} \rightarrow \ \phi ^ {0} / \phi ^ {1} \rightarrow 0 $$
is an algebraic version of the Gauss–Manin connection.
The Gauss–Manin connection is regular singular [a5]–[a8]. Its monodromy transformations around points at infinity are quasi-unipotent [a6], [a9], [a10], and bounds on the size of its Jordan blocks are known [a7], [a11]. Geometrical proofs of the monodromy theorem are due to A. Landman [a12], C.H. Clemens [a13] and D.T. Lê [a14].
Another important feature of the Gauss–Manin connection is Griffiths' transversality. The relative de Rham cohomology sheaves of a smooth proper morphism $ f: X \rightarrow S $ can be filtered as follows. Let $ F ^ { p } \Omega _ {X/S} ^ {\bullet } $ be the subcomplex
$$ [ 0 \rightarrow \dots \rightarrow 0 \rightarrow \ \Omega _ {X/S} ^ {p} \rightarrow \ \Omega _ {X/S} ^ {p + 1 } \rightarrow \dots ] $$
of $ \Omega _ {X/S} ^ {\bullet } $. Then $ \mathop{\rm Gr} _ {F} ^ { p } \Omega _ {X/S} ^ {\bullet } \cong \Omega _ {X/S} ^ {p} [- p] $. The spectral sequence $ E _ {1} ^ {pq} = R ^ {q} f _ \star \Omega _ {X/S} ^ {p} \Rightarrow H _ { \mathop{\rm dR} } ^ {p + q } ( X/S) $ degenerates at $ E _ {1} $[a15] and $ E _ {1} ^ {pq} $ is locally free on $ S $. Hence $ R ^ {n} f _ \star ( F ^ { p } \Omega _ {X/S} ^ {\bullet } ) $ maps injectively to a subsheaf $ F ^ { p } H _ { \mathop{\rm dR} } ^ {n} ( X/S) $ of $ H _ { \mathop{\rm dR} } ^ {n} ( X/S) $. Griffiths' transversality is the property that
$$ \nabla ( F ^ { p } H _ { \mathop{\rm dR} } ^ {n} ( X/S)) \subseteq \ \Omega _ {S} ^ {1} \otimes F ^ { p - 1 } H _ { \mathop{\rm dR} } ^ {n} ( X/S). $$
The geometric data $ ( H _ { \mathop{\rm dR} } ^ {n} ( X/S), \nabla , F ) $ have given rise to the concept of a (polarized) variation of Hodge structure. A. Borel has extended the monodromy theorem to this abstract case ([a16], (6.1)).
The Gauss–Manin connection has also been defined for function germs with isolated singularity [a10] and for mapping germs defining isolated complete intersection singularities [a17]. The monodromy of these connections is the classical Picard–Lefschetz monodromy on the vanishing cohomology.
In the theory of $ D $- modules (cf. $ D $- module), the theory of the Gauss–Manin connection is expressed as a property of the direct image functor for a proper morphism. Combined with the formalism of vanishing cycle functors [a18] it gives rise to the notion of the Gauss–Manin system [a19]. This plays an important role in the asymptotic Hodge theory of singularities [a20]–[a22].
References
| [a1] | Yu. Manin, "Algebraic curves over fields with differentiation" Transl. Amer. Math. Soc. , 37 (1964) pp. 59–78 Izv. Akad. Nauk. SSSR Ser. Mat. , 22 (1958) pp. 737–756 |
| [a2] | N.M. Katz, "On the differential equations satisfied by period matrices" Publ. Math. IHES , 35 (1968) pp. 71–106 |
| [a3] | A. Grothendieck, "On the de Rham cohomology of algebraic varieties" Publ. Math. IHES , 29 (1966) pp. 351–359 MR0199194 Zbl 0145.17602 |
| [a4] | N.M. Katz, T. Oda, "On the differentiation of de Rham cohomology classes with respect to parameters" J. Math. Kyoto Univ. , 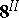 (1968) pp. 199–213 (1968) pp. 199–213 |
| [a5] | N. Nilsson, "Some growth and ramification properties of certain integrals on algebraic manifolds" Arkiv för Mat. , 5 (1963–1965) pp. 527–540 |
| [a6] | P. Deligne, "Equations différentielles à points singuliers réguliers" , Lect. notes in math. , 163 , Springer (1970) MR0417174 Zbl 0244.14004 |
| [a7] | N.M. Katz, "The regularity theorem in algebraic geometry" , Proc. Internat. Congress Mathematicians (Nice, 1970) , 1 , Gauthier-Villars (1971) pp. 437–443 |
| [a8] | P.A. Griffiths, "Periods of integrals on algebraic manifolds, I, II" Amer. J. Math. , 90 (1968) pp. 568–626; 805–865 |
| [a9] | A. Grothendieck, "Letter to J.-P. Serre" (5.10.1964) |
| [a10] | E. Brieskorn, "Die Monodromie von isolierten Singularitäten von Hyperflächen" Manuscr. Math. , 2 (1970) pp. 103–161 |
| [a11] | N.M. Katz, "Nilpotent connections and the monodromy theorem. Applications of a result of Turrittin" Publ. Math. IHES , 39 (1971) pp. 175–232 |
| [a12] | A. Landman, "On the Picard–Lefschetz formula for algebraic manifolds acquiring general singularities" , Berkeley (1967) (Thesis) |
| [a13] | C.H. Clemens, "Picard–Lefschetz theorem for families of nonsingular algebraic varieties acquiring ordinary singularities" Trans. Amer. Math. Soc. , 136 (1969) pp. 93–108 MR0233814 Zbl 0185.51302 |
| [a14] | D.T. Lê, "The geometry of the monodromy theorem" K.G. Ramanathan (ed.) , C.P. Ramanujam, a tribute , Tata IFR Studies in Math. , 8 , Springer (1978) |
| [a15] | P. Deligne, "Théorème de Lefschetz et critères de dégénérescence de suites spectrales" Publ. Math. IHES , 35 (1968) pp. 107–126 |
| [a16] | W. Schmid, "Variation of Hodge structure: the singularities of the period mapping" Invent. Math. , 22 (1973) pp. 211–319 MR0382272 Zbl 0278.14003 |
| [a17] | G.-M. Greuel, "Der Gauss–Manin Zusammenhang isolierter Singularitäten von vollständigen Durchschnitten" Math. Ann. , 214 (1975) pp. 235–266 |
| [a18] | P. Deligne, "Le formalisme des cycles évanescents" A. Grothendieck (ed.) , Groupes de monodromie en géométrie algébrique. SGA 7.II , Lect. notes in math. , 340 , Springer (1973) pp. Exp. XIII |
| [a19] | F. Pham, "Singularités des systèmes différentiels de Gauss–Manin" , Birkhäuser (1979) MR553954 Zbl 0524.32015 |
| [a20] | J. Scherk, J.H.M. Steenbrink, "On the mixed Hodge structure on the cohomology of the Milnor fibre" Math. Ann. , 271 (1985) pp. 641–665 |
| [a21] | A.N. Varchenko, "Asymptotic Hodge structure in the vanishing cohomology" Math USSR Izv. , 18 (1982) pp. 469–512 Izv. Akad. Nauk SSSR , 45 : 3 (1981) pp. 540–591; 688 |
| [a22] | M. Saito, "Gauss–Manin system and mixed Hodge structure" Proc. Japan Acad. Ser A , 58 (1982) pp. 29–32 |
Gauss–Manin connection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gauss%E2%80%93Manin_connection&oldid=22498