Furuta inequality
The Furuta inequality arose in the latter half of the 20th century in operator theory and is a beautiful extension of the Löwner–Heinz inequality. In the sequel, a capital letter denotes a bounded linear operator on a Hilbert space $ H $.
An operator $ T $
is said to be positive (denoted by $ T \geq 0 $)
if $ ( {Tx } , x ) \geq 0 $
for all $ x \in H $.
The Löwner–Heinz inequality, discovered in 1934, asserts the following:
a) $ A \geq B \geq 0 $ ensures $ A ^ \alpha \geq B ^ \alpha $ for all $ \alpha \in [ 0,1 ] $;
b) $ A \geq B \geq 0 $ does not always ensure $ A ^ {p} \geq B ^ {p} $ for all $ p > 1 $. Note that b) is an immediate consequence of a).
T. Furuta gained an insight into the striking contrast between a) and b), which appeared on the stage of operator inequalities as the following order-preserving operator inequality (Furuta inequality, 1987): If $ A \geq B \geq 0 $, then for each $ r \geq 0 $, $ p \geq 0 $, $ q \geq 1 $ with $ ( 1 + 2r ) q \geq p + 2r $:
i) $ ( B ^ {r} A ^ {p} B ^ {r} ) ^ {1/q } \geq ( B ^ {r} B ^ {p} B ^ {r} ) ^ {1/q } $; and
ii) $ ( A ^ {r} A ^ {p} A ^ {r} ) ^ {1/q } \geq ( A ^ {r} B ^ {p} A ^ {r} ) ^ {1/q } $.
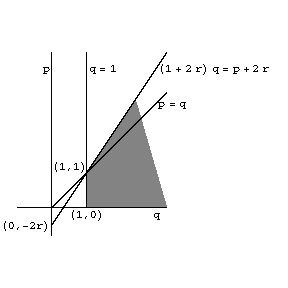
Figure: f110220a
The Furuta inequality yields a) by putting $ r = 0 $ in i) or ii). It should be understood as follows: One first makes the magic boxes
$$ f ( \square ) = ( B ^ {r} \square B ^ {r} ) ^ {1/q } \textrm{ and } g ( \square ) = ( A ^ {r} \square A ^ {r} ) ^ {1/q } . $$
Then $ f ( A ^ {p} ) \geq f ( B ^ {p} ) $ and $ g ( A ^ {p} ) \geq g ( B ^ {p} ) $ hold under the condition stated above. Consequently, the Furuta inequality is an extension of the Löwner–Heinz inequality and $ f ( \square ) $ and $ g ( \square ) $ can be considered as order-preserving operator functions related to b).
The original proof of the Furuta inequality is in [a5]; mean-theoretic alternative proofs are in [a3], [a8] and an elementary one-page proof is in [a6]. The domain drawn for $ p $, $ q $ and $ r $ in Fig.a1 is the best possible one for the Furuta inequality, see [a10]. It turned out that the Furuta inequality can be applied in the theories of operator inequalities, norm inequalities and operator equations. Some examples are given below.
Example 1.
(Theory of operator inequalities.) T. Ando [a1] has proved that the following assertions are equivalent:
1) $ { \mathop{\rm log} } A \geq { \mathop{\rm log} } B $;
2) $ A ^ {p} \geq ( A ^ {p/2 } B ^ {p} A ^ {p/2 } ) ^ {1/2 } $ for all $ p \geq 0 $;
3) $ A ^ {- p/2 } ( A ^ {p/2 } B ^ {p} A ^ {p/2 } ) ^ {1/2 } A ^ {- p/2 } $ is a decreasing function of $ p \geq 0 $.
An extension of Ando's result is the Fujii–Furuta–Kamei theorem, which states that the following assertions are equivalent:
1) $ { \mathop{\rm log} } A \geq { \mathop{\rm log} } B $;
2) $ A ^ {p} \geq ( A ^ {p/2 } B ^ {s} A ^ {p/2 } ) ^ {p/ ( p + s ) } $ for all $ p \geq 0 $ and all $ s \geq 0 $;
3) $ A ^ {- r/2 } ( A ^ {r/2 } B ^ {p} A ^ {r/2 } ) ^ {( t + r ) / ( p + r ) } A ^ {- r/2 } $ is a decreasing function of both $ p \geq t $ and $ r \geq 0 $ for any fixed $ t \geq 0 $.
Example 2.
(Theory of operator inequalities.) This examples concerns the estimation of the value of the relative operator entropy, defined by $ S ( A \mid B ) = A ^ {1/2 } ( { \mathop{\rm log} } A ^ {- 1/2 } BA ^ {- 1/2 } ) A ^ {1/2 } $ for positive invertible operators $ A $ and $ B $. One has $ { \mathop{\rm log} } C \geq { \mathop{\rm log} } A \geq { \mathop{\rm log} } B $ if and only if $ S ( A ^ {- p } \mid C ^ {s} ) \geq S ( A ^ {- p } \mid A ^ {s} ) \geq S ( A ^ {- p } \mid B ^ {s} ) $ for all $ p \geq 0 $ and all $ s \geq 0 $.
Example 3.
(Theory of operator inequalities.) Ando and F. Hiai [a2] established the following useful and interesting inequality, equivalent to log majorization (the Ando–Hiai inequality): If $ A \geq B \geq 0 $ with $ A > 0 $, then
$$ A ^ {r} \geq \left \{ A ^ {r/2 } ( A ^ {- 1/2 } B ^ {p} A ^ {- 1/2 } ) ^ {r} A ^ {r/2 } \right \} ^ {1/p } $$
for all $ p \geq 1 $ and $ r \geq 1 $. The following inequality, proved in [a7], interpolates between the Furuta inequality and the inequality stated above. The grand Furuta inequality (1995): If $ A \geq B \geq 0 $ with $ A > 0 $, then for each $ t \in [ 0,1 ] $ and $ p \geq 1 $,
$$ F _ {p,t } ( A,B,r,s ) = $$
$$ = A ^ {- r/2 } \left \{ {A ^ {r/2 } ( A ^ {- t/2 } B ^ {p} A ^ {- t/2 } ) ^ {s} A ^ {r/2 } } \right \} ^ { { \frac{1 - t + r }{( p - t ) s + r } } } A ^ {- r/2 } $$
is a decreasing function of both $ r $ and $ s $ for any $ s \geq 1 $ and $ r \geq t $, and the following inequality holds:
$$ A ^ {1 - t } = F _ {p,t } ( A,A,r,s ) \geq F _ {p,t } ( A,B,r,s ) $$
for any $ s \geq 1 $, $ p \geq 1 $, $ r \geq t $.
The mean-theoretic approach has also some advantages [a4]. See [a9] for the theory of operator means, in which the correspondence between non-negative operator monotone functions on $ ( 0, \infty ) $ and operator means is given.
Examples in the theory of norm inequalities are given by generalizations of the Heinz–Kato inequality and a generalization of the Kosaki trace inequality and related trace inequalities. Examples in the theory of operator equations are a generalization of the Pedersen–Takesaki theorem, which is closely related to a non-commutative Radon–Nikodým theorem, and related results.
See also Löwner–Heinz inequality.
References
| [a1] | T. Ando, "Some operator inequalities" Math. Ann. , 279 (1987) pp. 157–159 |
| [a2] | T. Ando, F. Hiai, "Log majorization and complementary Golden–Thompson type inequality" Linear Alg. & Its Appl. , 197/198 (1994) pp. 113–131 |
| [a3] | M. Fujii, "Furuta's inequality and its mean theoretic approach" J. Operator Th. , 23 (1990) pp. 67–72 |
| [a4] | M. Fujii, E. Kamei, "Mean theoretic approach to the grand Furuta inequality" Proc. Amer. Math. Soc. , 124 (1996) pp. 2751–2756 |
| [a5] | T. Furuta, "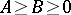 assures assures 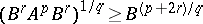 for for 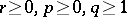 with with  " Proc. Amer. Math. Soc. , 101 (1987) pp. 85–88 " Proc. Amer. Math. Soc. , 101 (1987) pp. 85–88 |
| [a6] | T. Furuta, "Elementary proof of an order preserving inequality" Proc. Japan Acad. , 65 (1989) pp. 126 |
| [a7] | T. Furuta, "Extension of the Furuta inequality and Ando–Hiai log-majorization" Linear Alg. & Its Appl. , 219 (1995) pp. 139–155 |
| [a8] | E. Kamei, "A satellite to Furuta's inequality" Math. Japon. , 33 (1988) pp. 883–886 |
| [a9] | F. Kubo, T. Ando, "Means of positive linear operators" Math. Ann. , 246 (1980) pp. 205–224 |
| [a10] | K. Tanahashi, "Best possibility of the Furuta inequality" Proc. Amer. Math. Soc. , 124 (1996) pp. 141–146 |
Furuta inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Furuta_inequality&oldid=47029