Fresnel integrals
The special functions
$$ C ( x) = { \frac{1}{\sqrt {2 \pi } } } \int\limits _ { 0 } ^ { {x ^ {2}} } \frac{\cos t }{\sqrt t } dt = \ \sqrt { \frac{2} \pi } \int\limits _ { 0 } ^ { x } \cos t ^ {2} dt, $$
$$ S ( x) = { \frac{1}{\sqrt {2 \pi } } } \int\limits _ { 0 } ^ { {x } ^ {2} } \frac{\sin t }{\sqrt t } dt = \sqrt { \frac{2} \pi } \int\limits _ { 0 } ^ { x } \sin t ^ {2} dt; $$
$$ \lim\limits _ {x \rightarrow + \infty } C ( x) = \lim\limits _ {x \rightarrow + \infty } S ( x) = { \frac{1}{2} } . $$
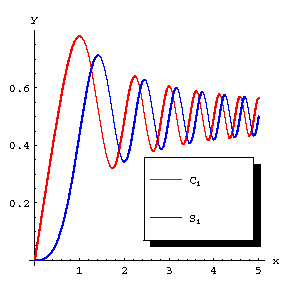
Figure: f041720a
The Fresnel integrals can be represented in the form of the series
$$ C ( x) = \sqrt { \frac{2} \pi } x \sum _ {k = 0 } ^ \infty \frac{(- 1) ^ {k} x ^ {4k} }{( 2k)! ( 4k + 1) } , $$
$$ S ( x) = \sqrt { \frac{2} \pi } x \sum _ {k = 0 } ^ \infty \frac{(- 1) ^ {k} x ^ {2 ( 2 k + 1) } }{( 2k + 1)! ( 4k + 3) } . $$
An asymptotic representation for large $ x $ is:
$$ C ( x) = { \frac{1}{2} } + \frac{1}{\sqrt {2 \pi } x } \ \sin x ^ {2} + O \left ( \frac{1}{x ^ {2} } \right ) , $$
$$ S ( x) = { \frac{1}{2} } - \frac{1}{\sqrt {2 \pi } x } \cos x ^ {2} + O \left ( \frac{1}{x ^ {2} } \right ) . $$
In a rectangular coordinate system $ ( x, y) $ the projections of the curve
$$ x = t,\ \ y = C \left ( { \frac \pi {2} } t ^ {2} \right ) ,\ \ z = S \left ( { \frac \pi {2} } t ^ {2} \right ) , $$
where $ t $ is a real parameter, onto the coordinate planes are the Cornu spiral and the curves $ y = C ( \pi t ^ {2} /2) $, $ z = S ( \pi t ^ {2} /2) $( see Fig. b). $ x $ $ S( x) $ $ C( x) $

Figure: f041720b
The generalized Fresnel integrals (see [1]) are functions of the form
$$ C ( x, \alpha ) = \ \int\limits _ { x } ^ \infty t ^ {\alpha - 1 } \ \cos t dt, $$
$$ S ( x, \alpha ) = \int\limits _ { x } ^ \infty t ^ {\alpha - 1 } \sin t dt. $$
The Fresnel integrals are related to the generalized Fresnel integrals as follows:
$$ C ( x) = { \frac{1}{2} } - \frac{1}{\sqrt {2 \pi } } C \left ( x ^ {2} , { \frac{1}{2} } \right ) ; $$
$$ S ( x) = { \frac{1}{2} } - \frac{1}{\sqrt {2 \pi } } S \left ( x ^ {2} , { \frac{1}{2} } \right ) . $$
References
| [1] | H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , Higher transcendental functions , 2. Bessel functions, parabolic cylinder functions, orthogonal polynomials , McGraw-Hill (1953) |
| [2] | E. Jahnke, F. Emde, "Tables of functions with formulae and curves" , Dover, reprint (1945) (Translated from German) |
Comments
A word of warning. There are different normalizations in use for the Fresnel integrals. E.g., in [a3] they are defined as
$$ C _ {1} ( z) = \int\limits _ { 0 } ^ { z } \cos \frac{\pi t ^ {2} }{2} d t ,\ S _ {1} ( z) = \ \int\limits _ { 0 } ^ { z } \sin \frac{\pi t ^ {2} }{2} d t , $$
so that
$$ C _ {1} ( z) = C \left ( \sqrt { \frac \pi {2} } z \right ) \ \ \textrm{ and } \ \ S _ {1} ( z) = S \left ( \sqrt { \frac \pi {2} } z \right ) . $$
The Fresnel integrals defined in the article are related to the probability integral for a complex argument $ z = \sqrt i x $,
$$ \Phi ( z) = \frac{2}{\sqrt \pi } \int\limits _ { 0 } ^ { z } e ^ {- t ^ {2} } d t $$
(integration along the line $ \mathop{\rm Re} z = \mathop{\rm Im} z $), by
$$ \frac{\Phi ( \sqrt i x ) }{\sqrt i } = \ \sqrt 2 C ( x) - i \sqrt 2 S ( x) . $$
References
| [a1] | A. Segun, M. Abramowitz, "Handbook of mathematical functions" , Appl. Math. Ser. , 55 , Nat. Bur. Standards (1970) |
| [a2] | J. Spanier, K.B. Oldham, "An atlas of functions" , Hemisphere & Springer (1987) pp. Chapt. 39 |
| [a3] | N.N. Lebedev, "Special functions and their applications" , Dover, reprint (1972) pp. 21–33 (Translated from Russian) |
Fresnel integrals. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fresnel_integrals&oldid=46990