Figà-Talamanca algebra
Let $G$ be a locally compact group, $1 < p < \infty$ and $p ^ { \prime } = p / p - 1$. Consider the set $\mathcal{A} _ { p } ( G )$ of all pairs $( ( k _ { n } ) _ { n = 1 } ^ { \infty } , ( l _ { n } ) _ { n = 1 } ^ { \infty } )$, with $( k _ { n } ) _ { n = 1 } ^ { \infty }$ a sequence in ${\cal L} _ {\bf C } ^ { p } ( G )$ and $( l _ { n } ) _ { n = 1 } ^ { \infty } $ a sequence in $\mathcal{L} _ { \text{C} } ^ { p ^ { \prime } } ( G )$ such that $\sum _ { n = 1 } ^ { \infty } N _ { p } ( k _ { n } ) N _ { p^{\prime} } ( l _ { n } ) < \infty$. Here, $N _ { p } ( f )$ is defined by $N _ { p } ( f ) = ( \int _ { G } | f ( x ) | ^ { p } d m ( x ) ) ^ { 1 / p }$, where $m$ is some left-invariant Haar measure on $G$. Let $A _ { p } ( G )$ denote the set of all $u \in {\bf C} ^ { G }$ for which there is a pair $( ( k _ { n } ) _ { n = 1 } ^ { \infty } , ( l _ { n } ) _ { n = 1 } ^ { \infty } ) \in \mathcal{A} _ { p } ( G )$ such that $u ( x ) = \sum _ { n = 1 } ^ { \infty } \overline { k _ { n } } * \check{l} _ { n } ( x )$, where $\check{\varphi} { P } ( x ) = \varphi ( x ^ { - 1 } )$. The set $A _ { p } ( G )$ is a linear subspace of the $\mathbf{C}$-vector space of all continuous complex-valued functions on $G$ vanishing at infinity. For $u \in A _ { p } ( G )$ one sets
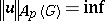 |
\begin{equation*} \left\{ \sum _ { n = 1 } ^ { \infty } N _ { p } ( k _ { n } ) N _ { p^{\prime} } ( l _ { n } ) : \begin{array} { c c } {((k_n)^{\infty}_{n=1} , (l_n)^{\infty}_{n=1}) \in \mathcal{A}_{p} (G) } \\ {\text { with } u = \sum _ { n = 1 } ^ { \infty } \overline { k _ { n } } * \check{l}_ { n }} \end{array} \right\}. \end{equation*}
1) For the pointwise product on $G$, $A _ { p } ( G )$ is a Banach algebra. This algebra is called the Figà-Talamanca algebra of $G$. If $G$ is Abelian, $A _ { 2 } ( G )$ is isometrically isomorphic to $L _ { \text{C} } ^ { 1 } ( \hat { G } )$, where $\hat { C }$ is the dual group of $G$. For $G$ not necessarily Abelian, $A _ { 2 } ( G )$ is precisely the Fourier algebra of $G$.
2) If $G$ is amenable, then $A _ { 2 } ( G ) \subset A _ { p } ( G )$. The algebra $A _ { p } ( G )$ is a useful tool for studying the $p$-convolution operators of $G$ (see [a2], [a7], [a8]). For a function $\varphi$ on $G$ and $a , x \in G$ one sets $\square_{a} \varphi ( x ) = \varphi ( a x )$. A continuous linear operator $T$ on $L _ { \text{C} } ^ { p } ( G )$ is said to be a $p$-convolution operator of $G$ if $T ( \square _ { \alpha } \varphi ) = \square _ { \alpha } ( T ( \varphi ) )$ for every $a \in G$ and every $\varphi \in L _ { \text{C} } ^ { p } ( G )$. Let $C V _ { p } ( G )$ be the set of all $p$-convolution operators of $G$. It is a closed subalgebra of the Banach algebra $\mathcal{L} ( L _ { \text{C} } ^ { p } ( G ) )$ of all continuous linear operators on $L _ { \text{C} } ^ { p } ( G )$. For a complex bounded measure $\mu$ on $G$ (i.e. $\mu \in M _ { \text{C} } ^ {1} ( G )$) and a continuous complex-valued function $\varphi$ with compact support on $G$ ($\varphi \in C _ { 00 } ( G ; \mathbf C )$), the rule $\lambda ^ { p } ( \mu ) [ \varphi ] = [ \varphi * \Delta _ { G } ^ { 1 / p ^ { \prime } } \check{\mu} ]$ defines a $p$-convolution operator $\lambda ^ { p } ( \mu )$. Of course, for $f \in \mathbf{C} ^ { G }$, $[ f ]$ denotes the set of all $g \in \mathbf{C} ^ { G }$ with $g ( x ) = f ( x )$ $m$-almost everywhere.
Even for $G = \mathbf{R}$ one has $C V _ { p } ( G ) \neq \lambda ^ { p } ( M ^ { 1 } ( G ) )$. Let $P M _ { p } ( G )$ be the closure in $C V _ { p } ( G )$ of $\lambda ^ { p } ( M ^ { 1 } ( G ) )$ with respect to the ultraweak operator topology on $\mathcal{L} ( L _ { \text{C} } ^ { p } ( G ) )$.
3) The dual $A _ { p } ( G ) ^ { \prime }$ of the Banach space $A _ { p } ( G )$ is canonically isometrically isomorphic to $P M _ { p } ( G )$. Also, $A _ { p } ( G ) ^ { \prime }$ with the topology $\sigma ( A _ { p } ( G ) ^ { \prime } , A _ { p } ( G ) )$ is homeomorphic to $P M _ { p } ( G )$ with the ultraweak operator topology on $\mathcal{L} ( L _ { \text{C} } ^ { p } ( G ) )$. As a consequence, for $G$ amenable or for $G$ arbitrary but with $p = 2$, $P M _ { p } ( G ) = C V _ { p } ( G )$.
This duality between $A _ { p } ( G )$ and $P M _ { p } ( G )$ also permits one to develop (see [a1]) a kind of "non-commutative harmonic analysis on G" , where (for $G$ Abelian) $A _ { p } ( G )$ replaces $L _ { \text{C} } ^ { 1 } ( \hat { G } )$ and $C V _ { p } ( G )$ replaces $L _ { C } ^ { \infty } ( \hat { G } )$. (Cf. also Harmonic analysis, abstract.)
Let $T \in C V _ { p } ( G )$. Then the support of $T$, denoted by 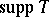 , is the set of all $x \in G$ for which for all open subsets $U$, $V$, of $G$ with $e \in U$ and $x \in \mathbf{V}$ there are $\phi , \psi \in C _ { 00 } ( G ; \mathbf{C} )$ with $\text{supp}\, \phi \subset U$, $\operatorname{supp} \psi \subset V$ and
, is the set of all $x \in G$ for which for all open subsets $U$, $V$, of $G$ with $e \in U$ and $x \in \mathbf{V}$ there are $\phi , \psi \in C _ { 00 } ( G ; \mathbf{C} )$ with $\text{supp}\, \phi \subset U$, $\operatorname{supp} \psi \subset V$ and
\begin{equation*} \langle T [ \phi ] , [ \psi ] \rangle _ { L _ { \text{C} } ^ { p } ( G ) , L _ { \text{C} } ^ { p^{\prime} } ( G ) } \neq 0. \end{equation*}
If $\mu \in M _ { \text{C} } ^ {1} ( G )$, then $\operatorname {supp}\lambda _ { G } ^ { p } ( \mu ) = ( \operatorname { supp } \mu ) ^ { - 1 }$. For $G$ Abelian, let $\varepsilon$ be the canonical mapping from $G$ onto $\widehat {\widehat {G} }$. Then $f \mapsto ( \widehat { f } \circ \varepsilon )$, where $ \check{\varphi} ( \chi ) = \varphi ( \chi ^ { - 1 } )$, is an isometric isomorphism of the Banach algebra $L ^ { 1 } ( \hat { G } )$ onto $A _ { 2 } ( G )$. Let $u \in L _ { \text{C} } ^ { \infty } ( \hat { G } )$ and $x \in G$. Then $x$ "belongs to the spectrum of u" (written as $x \in \operatorname { sp } u$) if $[ \epsilon ( x ) ]$ lies in the linear closure of $\left\{ \square _ { \chi } u : \chi \in \widehat { G } \right\}$ in $L _ { C } ^ { \infty } ( \hat { G } )$, for the weak topology $\sigma ( L _ {\bf C } ^ { \infty } ( \hat { G } ) , L _ {\bf C } ^ { 1 } ( \hat { G } ) )$. Let $T \in C V _ { p } ( G )$; then $\operatorname {sp} \hat { T } = ( \operatorname { supp } T ) ^ { - 1 }$. For $G$ not necessarily amenable and $T \in C V _ { p } ( G )$, $T = 0$ if and only 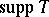 is empty. This assertion is a non-commutative version of the Wiener theorem! Similarly, there is also a version of the Carleman–Kaplansky theorem: for $T \in C V _ { p } ( G )$, $\operatorname { supp } T = \{ x _ { 1 } , \dots , x _ { n } \}$ if and only there exist $c_1 , \ldots , c_n \in \mathbf{C}$ such that $T = c _ { 1 } \lambda ^ { p } ( \delta _ { x _ { 1 } } ) + \ldots + c _ { n } \lambda ^ { p } ( \delta _ { x _ { n } } )$, where $\delta _ { x }$ denotes the Dirac measure in $x$ (cf. also Dirac distribution). In fact, even for $G = \mathbf{T}$ or for $G = \mathbf{R}$ (but $p \neq 2$) the situation is not classical!
is empty. This assertion is a non-commutative version of the Wiener theorem! Similarly, there is also a version of the Carleman–Kaplansky theorem: for $T \in C V _ { p } ( G )$, $\operatorname { supp } T = \{ x _ { 1 } , \dots , x _ { n } \}$ if and only there exist $c_1 , \ldots , c_n \in \mathbf{C}$ such that $T = c _ { 1 } \lambda ^ { p } ( \delta _ { x _ { 1 } } ) + \ldots + c _ { n } \lambda ^ { p } ( \delta _ { x _ { n } } )$, where $\delta _ { x }$ denotes the Dirac measure in $x$ (cf. also Dirac distribution). In fact, even for $G = \mathbf{T}$ or for $G = \mathbf{R}$ (but $p \neq 2$) the situation is not classical!
The Banach space $A _ { p } ( G )$ has been first introduced by A. Figà-Talamanca in [a3] for $G$ Abelian or $G$ non-Abelian but compact. For these classes of groups he obtained assertion 3) above. The statement for a general locally compact group is due to C.S. Herz [a5]. Assertion 1) is also due to Herz [a4].
The Banach algebra $A _ { p }$ also satisfies the following properties:
a) Let $H$ be a closed subgroup of $G$. Then $\operatorname { Res } _ { H } A _ { p } ( G ) = A _ { p } ( H )$. More precisely, for every $u \in A _ { p } ( H )$ and for every $\epsilon > 0$ there is a $v \in A _ { p } ( G )$ with $\operatorname { Res } _ { H } v = u$ and $\|v\|_{A_p (G)} \leq \| u \| _ { A_p(H) } + \epsilon$ (see [a5]).
b) The Banach algebra $A _ { p } ( G )$ has bounded approximate units (i.e. there is a $C > 0$ such that for every $u \in A _ { p } ( G )$ and for every $\epsilon > 0$ there is a $v \in A _ { p } ( G )$ with $\|v \| _ { A _ { p } ( G ) } \leq C$ and $\| u - u v \| _ { A _ { p } ( G ) } < \epsilon$) if and only if the locally compact group $G$ is amenable (see [a5] and [a6] for $p = 2$). This algebra is often called the Figà-Talamanca–Herz algebra.
See also Fourier algebra.
References
| [a1] | A. Derighetti, "Quelques observations concernant les ensembles de Ditkin d'un groupe localement compact" Monatsh. Math. , 101 (1986) pp. 95–113 |
| [a2] | P. Eymard, "Algèbres $A _ { p }$ et convoluteurs de $L ^ { p } ( G )$" , Sem. Bourbaki 1969/70, Exp. 367 , Lecture Notes in Math. , 180 , Springer (1971) pp. 364–381 |
| [a3] | A. Figà-Talamanca, "Translation invariant operators in $L ^ { p }$" Duke Math. J. , 32 (1965) pp. 495–501 |
| [a4] | C. Herz, "The theory of $p$-spaces" Trans. Amer. Math. Soc. , 154 (1971) pp. 69–82 |
| [a5] | C. Herz, "Harmonic synthesis for subgroups" Ann. Inst. Fourier (Grenoble) , 23 : 3 (1973) pp. 91–123 |
| [a6] | H. Leptin, "Sur l'algèbre de Fourier d'un groupe localement compact" C.R. Acad. Sci. Paris Sér. A , 266 (1968) pp. 1180–1182 |
| [a7] | N. Lohoué, "Algèbres $A _ { p }$ et convoluteurs de $L ^ { p } ( G )$" Thèse, Univ. Paris-Sud (1971) |
| [a8] | N. Lohoué, "Estimations $L ^ { p }$ des coefficients de représentations et opérateurs de convolution" Adv. Math. , 38 (1980) pp. 178–221 |
| [a9] | J.R. McMullen, "Extensions of positive-definite functions" Memoirs Amer. Math. Soc. , 117 (1972) |
| [a10] | J.-P. Pier, "Amenable locally compact groups" , Wiley (1984) |
Figà-Talamanca algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fig%C3%A0-Talamanca_algebra&oldid=55337