Evolutionarily stable strategy
Conflicts between organisms are often modelled as games (cf. also Games, theory of). Here, attention is confined to conflicts between con-specifics, which are also symmetric in the sense that each player has available the same set of strategies (cf. Strategy (in game theory)) and the same pay-off function. (Important texts in this area are [a5], [a8], [a15], [a17], [a22].)
Consider first two-player conflicts (cf. also Two-person zero-sum game). Suppose there exists a set of possible strategies 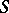 , and a pay-off function
, and a pay-off function 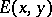 , where
, where  , the pay-off to a player who plays
, the pay-off to a player who plays  against one who plays
against one who plays 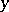 . One extends the set of available strategies to some
. One extends the set of available strategies to some 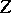 , where each
, where each 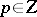 is a weight function defined on the elements of
is a weight function defined on the elements of 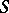 ; e.g. a probability function if
; e.g. a probability function if 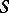 is discrete. One supposes that the extension of the pay-off function is linear, i.e. for
is discrete. One supposes that the extension of the pay-off function is linear, i.e. for 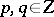 ,
,
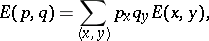 |
where 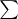 denotes summation or integration (as appropriate) and
denotes summation or integration (as appropriate) and 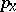 is the weight attached to
is the weight attached to  by
by 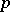 .
.
A concept of solution of an evolutionarily stable strategy was introduced in [a19]. Such a strategy, if adopted by the whole of the (infinite) population (see [a21] for the finite case), cannot be invaded by any alternate strategy introduced at low frequency.
A strategy 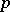 is said to be evolutionarily stable with respect to
is said to be evolutionarily stable with respect to 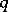 if:
if:
1) 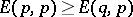 ;
;
2) 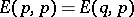 implies
implies 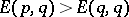 .
.
A strategy 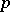 is said to be evolutionarily stable if
is said to be evolutionarily stable if 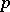 is evolutionarily stable with respect to
is evolutionarily stable with respect to 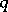 for all
for all 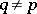 . For a discussion of the definition see also [a5] and [a23]. Let
. For a discussion of the definition see also [a5] and [a23]. Let 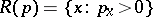 denote the support of
denote the support of 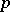 . If
. If 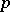 is such that
is such that 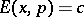 for all
for all 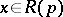 while
while 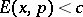 for all
for all 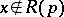 , then
, then 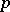 is a strict Nash equilibrium (cf. also Nash theorem (in game theory)). It follows that
is a strict Nash equilibrium (cf. also Nash theorem (in game theory)). It follows that 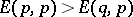 , so
, so 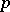 is evolutionarily stable against
is evolutionarily stable against 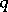 for all
for all 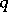 such that
such that 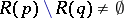 ,
, 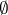 being the empty set. Thus, in the generic case an evolutionarily stable strategy is a strict Nash equilibrium with the additional condition that for all
being the empty set. Thus, in the generic case an evolutionarily stable strategy is a strict Nash equilibrium with the additional condition that for all 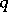 such that
such that 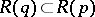 one requires that
one requires that 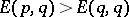 , or, equivalently, that for all
, or, equivalently, that for all 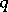 such that
such that 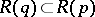 one requires that
one requires that 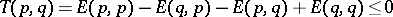 , with equality if and only if
, with equality if and only if  .
.
For conditions for 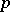 to be an evolutionarily stable strategy in the finite (i.e. matrix) case, see [a10] (generic) and [a1] (non-generic). If
to be an evolutionarily stable strategy in the finite (i.e. matrix) case, see [a10] (generic) and [a1] (non-generic). If 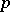 is an evolutionarily stable strategy and
is an evolutionarily stable strategy and 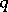 is such that
is such that 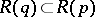 , then
, then 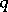 is not an evolutionarily stable strategy (the Bishop–Cannings theorem, [a4]).
is not an evolutionarily stable strategy (the Bishop–Cannings theorem, [a4]).
The war of attrition was introduced in [a16], where 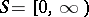 and
and 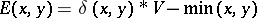 and
and 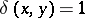 if
if 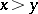 ,
, 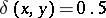 if
if 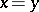 and
and 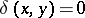 if
if 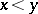 . Thus, individuals contest for a reward
. Thus, individuals contest for a reward 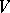 by choosing a single value, perhaps display time, the winner being the one choosing the larger value but the cost to each only being the lesser; i.e. the contest ends immediately when the first individual retreats. In this case there is a unique evolutionarily stable strategy, given by
by choosing a single value, perhaps display time, the winner being the one choosing the larger value but the cost to each only being the lesser; i.e. the contest ends immediately when the first individual retreats. In this case there is a unique evolutionarily stable strategy, given by 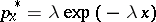 ,
, 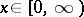 , where
, where 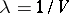 . This follows since
. This follows since 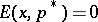 ,
, 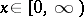 ,
, 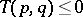 with equality if and only if
with equality if and only if  , which ensures that
, which ensures that 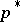 is an evolutionarily stable strategy, and this is unique by the Bishop–Cannings theorem. If
is an evolutionarily stable strategy, and this is unique by the Bishop–Cannings theorem. If 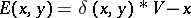 , i.e. individuals essentially commit themselves irrevocable to their choice, as might occur for a choice of size, then there is no evolutionarily stable strategy [a18]. A hybrid model with
, i.e. individuals essentially commit themselves irrevocable to their choice, as might occur for a choice of size, then there is no evolutionarily stable strategy [a18]. A hybrid model with 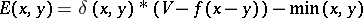 has been treated by [a12].
has been treated by [a12].
Finite conflicts.
As stated above, [a10] gives conditions in the finite (i.e. matrix) case for 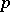 to be an evolutionarily stable strategy. Suppose
to be an evolutionarily stable strategy. Suppose 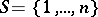 and
and 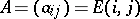 . For
. For 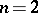 , an evolutionarily stable strategy with
, an evolutionarily stable strategy with 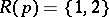 exists if and only if
exists if and only if 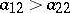 and
and 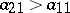 . See, in particular, [a19] for the hawk–dove scenario, where there is a reward
. See, in particular, [a19] for the hawk–dove scenario, where there is a reward 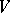 for winning, a hawk always beats a dove, doves share the reward, while hawks share the reward but also incur damage (cost
for winning, a hawk always beats a dove, doves share the reward, while hawks share the reward but also incur damage (cost 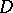 ). Thus,
). Thus,
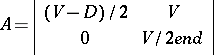 |
and there is an evolutionarily stable strategy with both hawk and dove if 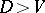 , demonstrating that organisms need not adopt aggressive strategies. On the other hand, if
, demonstrating that organisms need not adopt aggressive strategies. On the other hand, if 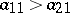 , then
, then 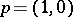 is an evolutionarily stable strategy, while if
is an evolutionarily stable strategy, while if 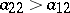 , then
, then 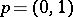 is an evolutionarily stable strategy. Thus there is always at least one evolutionarily stable strategy.
is an evolutionarily stable strategy. Thus there is always at least one evolutionarily stable strategy.
For 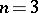 , [a10] has given examples of the possible sets of evolutionarily stable strategies, it being possible that there be no evolutionarily stable strategy. More generally, suppose that
, [a10] has given examples of the possible sets of evolutionarily stable strategies, it being possible that there be no evolutionarily stable strategy. More generally, suppose that 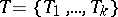 , where
, where 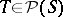 ,
, 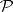 denoting the power set. Then
denoting the power set. Then 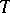 is called a pattern. If there exists an
is called a pattern. If there exists an 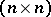 -matrix
-matrix 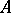 with
with 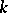 evolutionarily stable strategies with supports
evolutionarily stable strategies with supports 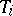 , then
, then 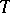 is said to be attainable on
is said to be attainable on 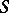 . The Bishop–Cannings theorem ensures that an attainable pattern is a Sperner family. Various restrictions on the set of attainable patterns have been derived in [a24]; in it, it is conjectured that if
. The Bishop–Cannings theorem ensures that an attainable pattern is a Sperner family. Various restrictions on the set of attainable patterns have been derived in [a24]; in it, it is conjectured that if 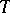 is attainable and
is attainable and 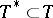 , then
, then 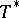 is also attainable on
is also attainable on 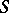 . This conjecture is still (1996) open, although in [a6] it has been proved that
. This conjecture is still (1996) open, although in [a6] it has been proved that 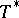 is attainable for some
is attainable for some 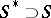 .
.
Dynamics.
A major criticisism of the evolutionarily stable strategy solution concept is that it is a static, rather than a dynamic concept. However, for the continuous replicator dynamics, if there is an interior evolutionarily stable strategy 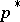 , then convergence to that evolutionarily stable strategy is assured, where
, then convergence to that evolutionarily stable strategy is assured, where 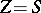 [a26], and, more generally, if
[a26], and, more generally, if 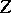 is such that
is such that 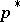 is a convex combination of some subset of its elements, then convergence is assured to the linear manifold defined by
is a convex combination of some subset of its elements, then convergence is assured to the linear manifold defined by 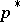 [a2]. If the players can choose
[a2]. If the players can choose 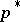 itself, then convergence is assured even for more general dynamics [a7]. For further discussion of dynamics see [a14], which uses a covariance approach and for an examination of the embedding of such dynamics within a genetic system, and a discussion of whether evolution can find the evolutionarily stable strategy, see [a9], [a13], [a25].
itself, then convergence is assured even for more general dynamics [a7]. For further discussion of dynamics see [a14], which uses a covariance approach and for an examination of the embedding of such dynamics within a genetic system, and a discussion of whether evolution can find the evolutionarily stable strategy, see [a9], [a13], [a25].
Iterated conflicts, spatial conflicts and cooperation.
The classic paradigm for examining the evolution of cooperation is the prisoner dilemma [a3] (see [a22] for an excellent overview). Here the defect strategy dominates the cooperate strategy (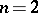 ). However, if the conflict consists not of a single play, but of a series of random (geometrically distributed) length, then cooperation can evolve. A series of strategies (tit-for-tat, i.e. imitate the opponent's last play, two-tits-for-tat, generous-tit-for-tat, etc.) has been developed, and although none of these is an evolutionarily stable strategy, studies suggest that cooperation, in some form, may evolve. In a related way, spatial structure (players are located at the points of a grid, interact with some set of neighbours and imitate the best local strategy in the next round) may lead to the persistence of both strategies [a20].
). However, if the conflict consists not of a single play, but of a series of random (geometrically distributed) length, then cooperation can evolve. A series of strategies (tit-for-tat, i.e. imitate the opponent's last play, two-tits-for-tat, generous-tit-for-tat, etc.) has been developed, and although none of these is an evolutionarily stable strategy, studies suggest that cooperation, in some form, may evolve. In a related way, spatial structure (players are located at the points of a grid, interact with some set of neighbours and imitate the best local strategy in the next round) may lead to the persistence of both strategies [a20].
Multi-player conflicts.
A multi-player war of attrition model is discussed in [a11]. This necessitates the extension of the notion of an evolutionarily stable strategy to 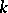 players. Assume that the pay-off for playing
players. Assume that the pay-off for playing 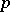 against
against 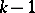 opponents depends only on the membership of the set of strategies and not on any ordering within the set. Thus, the pay-off to an individual who plays
opponents depends only on the membership of the set of strategies and not on any ordering within the set. Thus, the pay-off to an individual who plays 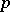 while
while 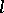 of the
of the 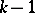 opponents play
opponents play 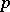 and
and 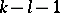 play
play 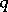 can be written as
can be written as 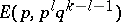 . A strategy
. A strategy 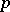 is said to be evolutionarily stable with respect to
is said to be evolutionarily stable with respect to 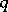 in a
in a 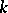 -player conflict if there exists a
-player conflict if there exists a 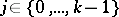 such that
such that
1) 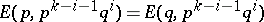 , for
, for 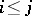 ;
;
2) 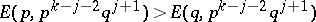 . An evolutionarily stable strategy is then defined as for the two-player conflict in terms of evolutionary stability. Note that the definition, while only referring to two strategies, implicitly deals with the case of several strategies. There are then situations in which no evolutionarily stable strategy exists in the war of attrition, e.g. if players are allowed to re-assess their play when some other player quits. It is clear that the study of multi-player conflicts and their application to the establishment and maintenance of dominance hierarchies, to mate selection, etc., is an area of considerable importance.
. An evolutionarily stable strategy is then defined as for the two-player conflict in terms of evolutionary stability. Note that the definition, while only referring to two strategies, implicitly deals with the case of several strategies. There are then situations in which no evolutionarily stable strategy exists in the war of attrition, e.g. if players are allowed to re-assess their play when some other player quits. It is clear that the study of multi-player conflicts and their application to the establishment and maintenance of dominance hierarchies, to mate selection, etc., is an area of considerable importance.
References
| [a1] | A. Abakucs, "Conditions for evolutionarily stable strategies" J. Appl. Probab. , 17 (1980) pp. 559–562 |
| [a2] | E. Akin, "Exponential families and game dynamics" Canadian J. Math. , 34 (1982) pp. 374–405 |
| [a3] | R. Axelrod, "Further evolution of co-operation" Science , 242 (1988) pp. 1385–1390 |
| [a4] | D.T. Bishop, C. Cannings, "A generalised war of attrition" J. Theor. Biol , 70 (1978) pp. 85–124 DOI 10.1016/0022-5193(78)90304-1 |
| [a5] | I.M. Bomze, B.M. Potschner, "Game theoretical foundations of evolutionary stability" , Lecture Notes Econom. and Math. Systems , Springer (1998) |
| [a6] | M. Broom, C. Cannings, G.T. Vickers, "Sequential methods in patterns of ESS's" J. Math. Biol. , 22 (1994) pp. 597–615 |
| [a7] | C. Cannings, "Topics in the theory of ESS's" S. Lessard (ed.) , Proc. NATO Advanced Study Institute (Montreal, 1987) , Kluwer Acad. Publ. (1990) |
| [a8] | R. Cressman, "The stability concept of evolutionary game theory" , Springer (1992) |
| [a9] | I. Eshel, M.W. Feldman, "Initial increase of new mutants and continuity properties of ESS in two-locus systems" Amer. Nat. , 124 (1984) pp. 631–640 |
| [a10] | J. Haigh, "Game theory and evolution" Advances Appl. Probab. , 7 (1975) pp. 8–10 |
| [a11] | J. Haigh, C. Cannings, "The $n$-person war of attrition" Acta Applic. Math. , 14 (1989) pp. 59–74 |
| [a12] | J. Haigh, M.R. Rose, "Evolutionary game auctions" J. Theor. Biol. , 85 (1980) pp. 381–397 |
| [a13] | P. Hammerstein, "Darwinian adaptation, population genetics and the streetcar theory of evolution" J. Math. Biol. , 34 (1996) pp. 511–532 |
| [a14] | W.G.S. Hines, D. Anfossi, "A discusson of evolutionarily stable strategies" S. Lessard (ed.) , Proc. NATO Adv. Study Inst. (Montreal, 1987) , Kluwer Acad. Publ. (1990) |
| [a15] | J. Hofbauer, K. Sigmund, "The theory of evolution and dynamical systems" , Cambridge Univ. Press (1988) |
| [a16] | J. Maynard Smith, "The theory of games and the evolution of animal conflicts" J. Theor. Biol. , ,47 (1974) pp. 209–221 DOI 10.1016/0022-5193(74)90110-6 |
| [a17] | J. Maynard Smith, "Evolution and the theory of games" , Cambridge Univ. Press (1982) |
| [a18] | J. Maynard Smith, G.E. Parker, "The logic of asymmetric conflicts" Animal Behavior , 24 (1976) pp. 159–175 |
| [a19] | J. Maynard Smith, G.R. Price, "The logic of animal conflict" Nature , 246 (1973) pp. 15–18 |
| [a20] | M.A. Nowak, R.M. May, "Evolutionary games and spatial chaos" Nature , 359 (1992) pp. 826–829 |
| [a21] | J.G. Riley, "Evolutionary equilibrium strategies" J. Theor. Biol. , 76 (1979) pp. 109–123 DOI 10.1016/0022-5193(79)90365-5 |
| [a22] | K. Sigmund, "Games of life" , Oxford Univ. Press (1993) |
| [a23] | G.T. Vickers, C. Cannings, "On the definition of an evolutionarily stable strategy" J. Theor. Biol. , 129 (1987) pp. 349–353 |
| [a24] | G.T. Vickers, C. Cannings, "Patterns of ESS's 1" J. Theor. Biol. , 132 (1988) pp. 387–408 |
| [a25] | F.J. Weissing, "Genetic versus phenotypic models of selection: Can genetics be neglected in a long term perspective?" J. Math. Biol. , 34 (1996) pp. 533–555 |
| [a26] | E.C. Zeeman, "Population dynamics from game theory" A. Nitecki (ed.) C. Robinson (ed.) , Global Theory of Dynamical Systems , Springer (1980) |
Evolutionarily stable strategy. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Evolutionarily_stable_strategy&oldid=39320