Edgeworth series
2020 Mathematics Subject Classification: Primary: 60F05 [MSN][ZBL]
The series defined by
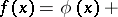 | (*) |
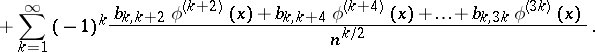 |
Here  is the distribution density of the random variable
is the distribution density of the random variable
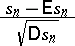 |
( , where
, where  are independent and identically distributed),
are independent and identically distributed),
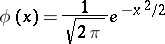 |
is the density of the standard normal distribution, and
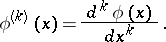 |
The coefficients  ,
, 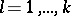 , do not depend on
, do not depend on  and are polynomials with respect to
and are polynomials with respect to 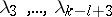 , where
, where  ,
, 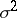 is the variance, and
is the variance, and 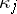 is the semi-invariant of order
is the semi-invariant of order 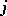 of
of 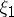 . In particular, the first terms of the expansion have the form
. In particular, the first terms of the expansion have the form
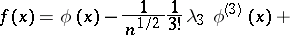 |
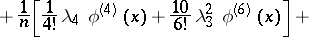 |
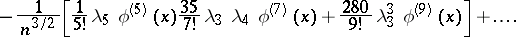 |
The coefficients 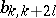 can also be expressed in terms of the central moments.
can also be expressed in terms of the central moments.
The series (*) were introduced by F.Y. Edgeworth [E]. Their asymptotic properties have been studied by H. Cramér, who has shown that under fairly general conditions the series (*) is the asymptotic expansion of 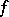 in which the remainder has the order of the first discarded term.
in which the remainder has the order of the first discarded term.
References
| [E] | F.Y. Edgeworth, "The law of error I" Proc. Cambridge Philos. Soc. , 20 (1905) pp. 36–65 |
| [C] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) MR0016588 Zbl 0063.01014 |
Comments
The above discussion omits many technical details as well as modern developments.
An excellent account of the theory of Edgeworth expansions for sums of independent random variables is given in [P]. See also [F], Chapt. XVI for a brief and very smooth introduction to the theory of Edgeworth expansions. The case of sums of independent random vectors is treated in [BR]. Extensions to statistics of a more complicated structure, such as 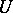 -statistics — which are especially of interest in statistical theory — were studied by many authors over the last 15 years (as of 1988). An important recent contribution in this area is [BGZ].
-statistics — which are especially of interest in statistical theory — were studied by many authors over the last 15 years (as of 1988). An important recent contribution in this area is [BGZ].
References
| [P] | V.V. Petrov, "Sums of independent random variables", Springer (1975) (Translated from Russian) MR0388499 Zbl 0322.60043 Zbl 0322.60042 |
| [F] | W. Feller, "An introduction to probability theory and its applications", 2, Wiley (1971) pp. 135 |
| [BR] | R.N. Bhattacharya, R. Ranga Rao, "Normal approximations and asymptotic expansions", Wiley (1976) MR0436272 |
| [BGZ] | P.J. Bickel, F. Götze, W.R. van Zwet, "The Edgeworth expansion for 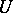 -statistics of degree two" Ann. Statist., 14 (1986) pp. 1463–1484 MR868312 -statistics of degree two" Ann. Statist., 14 (1986) pp. 1463–1484 MR868312
|
Edgeworth series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Edgeworth_series&oldid=26439