Diophantine approximations
The branch of number theory whose subject is the approximation of zero by values of functions of a finite number of integer arguments. The original problems of Diophantine approximations concerned rational approximations to real numbers, but the development of the theory gave rise to problems in which certain real functions must be assigned "small" values if the values of the arguments are integers. Accordingly, Diophantine approximations are closely connected with solving inequalities in integers — Diophantine inequalities — and also with solving equations in integers (cf. Diophantine equations).
If the (approximating) function under study
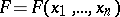 |
is linear with respect to the integer arguments  , then the Diophantine approximations with the function
, then the Diophantine approximations with the function 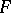 are said to be linear; otherwise they are called non-linear. If
are said to be linear; otherwise they are called non-linear. If  is a homogeneous polynomial in
is a homogeneous polynomial in  , the Diophantine approximations with the function
, the Diophantine approximations with the function 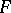 are said to be homogeneous. Several functions
are said to be homogeneous. Several functions 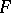 with at least one common integer argument may be studied at the same time. In such a case the Diophantine approximations are called simultaneous. Simultaneous Diophantine approximations may be linear or non-linear, homogeneous or inhomogeneous in the above sense.
with at least one common integer argument may be studied at the same time. In such a case the Diophantine approximations are called simultaneous. Simultaneous Diophantine approximations may be linear or non-linear, homogeneous or inhomogeneous in the above sense.
Numerical values of 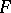 may be considered as being close to zero not only if
may be considered as being close to zero not only if
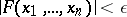 |
for a given 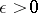 , but also if
, but also if
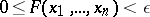 |
(one-sided approximations). The function 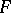 may depend on parameters which continuously vary in some domain; these are parametric Diophantine approximations. Finally, the domain of definition and the range of values of the approximating functions may be subsets not only of a Euclidean space, but also of altogether different topological spaces (see below: Diophantine approximations in
may depend on parameters which continuously vary in some domain; these are parametric Diophantine approximations. Finally, the domain of definition and the range of values of the approximating functions may be subsets not only of a Euclidean space, but also of altogether different topological spaces (see below: Diophantine approximations in 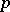 -adic number fields and Diophantine approximations in the field of power series).
-adic number fields and Diophantine approximations in the field of power series).
The oldest ( "simplest" ) problem in Diophantine approximations are approximations of zero by a linear form 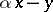 , where
, where 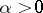 is a given real number and
is a given real number and  and
and 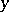 are variable integers (linear homogeneous Diophantine approximations), i.e. the problem of rational approximations to
are variable integers (linear homogeneous Diophantine approximations), i.e. the problem of rational approximations to 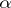 . For special
. For special 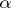 (
(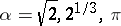 ) this problem had been considered even in Antiquity (Archimedes, Diophantus, Euclid), while its close connection with the theory of continued fractions (cf. Continued fraction) was completely clarified by L. Euler and J.L. Lagrange. In particular, if
) this problem had been considered even in Antiquity (Archimedes, Diophantus, Euclid), while its close connection with the theory of continued fractions (cf. Continued fraction) was completely clarified by L. Euler and J.L. Lagrange. In particular, if 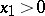 ,
, 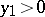 are such that
are such that
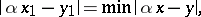 |
where the minimum is taken over all integers  in some arbitrary interval
in some arbitrary interval 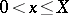 and over all integer values
and over all integer values 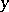 , the fraction
, the fraction 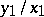 is a convergent fraction of the expansion of
is a convergent fraction of the expansion of  into a continued fraction. If the incomplete partial fractions of
into a continued fraction. If the incomplete partial fractions of  into a continued fraction are bounded, then there exists a
into a continued fraction are bounded, then there exists a 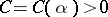 with the condition
with the condition 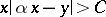 for all integers
for all integers 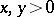 . This is true, for example, for quadratic irrationalities
. This is true, for example, for quadratic irrationalities 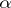 (cf. Quadratic irrationality), since then the expansion into a continued fraction is periodic. On the other hand, for any irrational number
(cf. Quadratic irrationality), since then the expansion into a continued fraction is periodic. On the other hand, for any irrational number 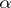 the inequality
the inequality 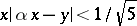 has an infinite number of integer solutions
has an infinite number of integer solutions 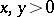 , and if
, and if  , the constant
, the constant 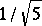 cannot be replaced by a smaller number. The study of A.A. Markov on the minima of indefinite binary quadratic forms (cf. Binary quadratic form) made it possible to extend this last statement: If
cannot be replaced by a smaller number. The study of A.A. Markov on the minima of indefinite binary quadratic forms (cf. Binary quadratic form) made it possible to extend this last statement: If 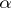 is not equivalent (in the sense of the theory of continued fractions) to
is not equivalent (in the sense of the theory of continued fractions) to 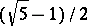 , then the inequality
, then the inequality 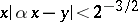 has an infinite number of solutions; the constant
has an infinite number of solutions; the constant 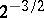 cannot be improved upon if
cannot be improved upon if 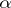 is equivalent to
is equivalent to 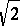 ; if
; if  is not equivalent either to
is not equivalent either to 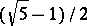 or to
or to 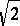 , the inequality
, the inequality 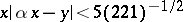 has an infinite number of solutions, etc. [1]. The constants
has an infinite number of solutions, etc. [1]. The constants 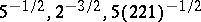 decrease monotonically and have limit
decrease monotonically and have limit 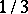 .
.
The simplest example of linear inhomogeneous Diophantine approximations are approximations of zero by a linear inhomogeneous polynomial  , where
, where 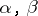 are real numbers and
are real numbers and 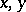 are integer variables. It was shown by P.L. Chebyshev that for any irrational number
are integer variables. It was shown by P.L. Chebyshev that for any irrational number 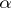 and any
and any 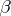 the inequality
the inequality 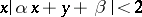 has an infinite number of solutions in integers
has an infinite number of solutions in integers 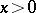 ,
, 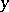 . In this case 2 is not the best constant: It was proved by H. Minkowski that if
. In this case 2 is not the best constant: It was proved by H. Minkowski that if 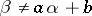 , where
, where 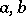 are integers, the constant 2 can be replaced by
are integers, the constant 2 can be replaced by 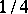 , the latter being the optimal constant. This statement is a corollary of the simplest case of a hypothesis on the product of inhomogeneous linear forms proved by H. Minkowski himself (cf. Minkowski hypothesis).
, the latter being the optimal constant. This statement is a corollary of the simplest case of a hypothesis on the product of inhomogeneous linear forms proved by H. Minkowski himself (cf. Minkowski hypothesis).
More complex problems of the general theory of Diophantine approximations concern the approximation of functions of a large number of integer arguments (cf. Dirichlet theorem; Minkowski theorem; Kronecker theorem). It is convenient to introduce the function 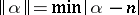 , where the minimum is taken over all integers
, where the minimum is taken over all integers  (the distance between
(the distance between 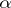 and the nearest integer). For instance, the above-mentioned linear polynomials
and the nearest integer). For instance, the above-mentioned linear polynomials 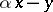 and
and  may be replaced by
may be replaced by 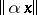 and
and 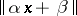 for integers
for integers 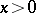 . It follows from Dirichlet's theorem that for all real
. It follows from Dirichlet's theorem that for all real  there exists an infinite number of solutions of the system of inequalities
there exists an infinite number of solutions of the system of inequalities
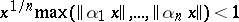 |
in integers 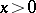 . Here, 1 may be replaced by a smaller number (e.g.
. Here, 1 may be replaced by a smaller number (e.g.  ), but the optimal constant is unknown for any
), but the optimal constant is unknown for any  (1988). It cannot be an arbitrary number, as is shown by the example of numbers
(1988). It cannot be an arbitrary number, as is shown by the example of numbers 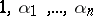 which form a basis of a real algebraic field [1]. If
which form a basis of a real algebraic field [1]. If 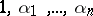 are linearly independent over the field of rational numbers, then for any
are linearly independent over the field of rational numbers, then for any 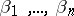 and any
and any 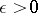 there exists an infinite number of solutions of the system of inequalities
there exists an infinite number of solutions of the system of inequalities
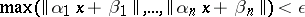 |
in integers 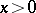 (Kronecker's theorem). An important feature of this theorem on simultaneous inhomogeneous Diophantine approximations consists in the fact that it is not possible, in principle (without special information on homogeneous approximations to
(Kronecker's theorem). An important feature of this theorem on simultaneous inhomogeneous Diophantine approximations consists in the fact that it is not possible, in principle (without special information on homogeneous approximations to  ), to find the rate of decrease of
), to find the rate of decrease of  as
as  increases: In order for linear forms
increases: In order for linear forms 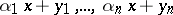 to represent a "good" approximation to arbitrary numbers
to represent a "good" approximation to arbitrary numbers 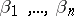 , it is necessary and sufficient for these forms not to be a "good" approximation for the special sample of numbers
, it is necessary and sufficient for these forms not to be a "good" approximation for the special sample of numbers 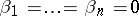 .
.
Problems in Diophantine approximations which are dissimilar at first sight sometimes turn out to be closely connected. For instance, Khinchin's transference principle [1] relates the solvability of the equation
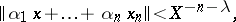 | (1) |
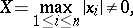 |
in integers  to that of the system
to that of the system
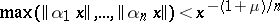 | (2) |
in integers 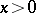 , and vice versa: If
, and vice versa: If 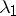 and
and 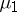 are, respectively, the least upper bounds of those
are, respectively, the least upper bounds of those 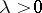 and
and 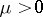 for which (1) and (2) have an infinite number of solutions, then
for which (1) and (2) have an infinite number of solutions, then
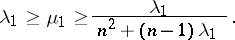 |
In particular, the equalities 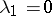 and
and 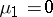 are equivalent (the
are equivalent (the  then represent the "worst" approximations, since equation (1) with
then represent the "worst" approximations, since equation (1) with 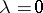 and equations (2) with
and equations (2) with 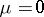 have an infinite number of solutions, whatever the values of
have an infinite number of solutions, whatever the values of  ). Similar relations exist between the homogeneous and the inhomogeneous problems [1], [5], and not only for linear Diophantine approximations. If, for instance,
). Similar relations exist between the homogeneous and the inhomogeneous problems [1], [5], and not only for linear Diophantine approximations. If, for instance,  are such that for any
are such that for any 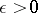 for all integers
for all integers 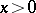 ,
,
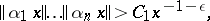 | (3) |
where 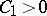 depends only on
depends only on  and
and  , then, for any real numbers
, then, for any real numbers 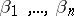 and any
and any 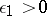 , the system of inequalities
, the system of inequalities
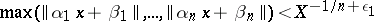 |
has an integer solution  subject to the condition
subject to the condition 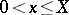 if
if 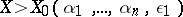 . Moreover, the inequality (3) ensures a "strong" uniform distribution of the fractional parts
. Moreover, the inequality (3) ensures a "strong" uniform distribution of the fractional parts 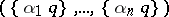 , where
, where  ; the number of these fractions comprised in the system of intervals
; the number of these fractions comprised in the system of intervals 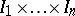 , each one of which is located inside the unit interval, is
, each one of which is located inside the unit interval, is 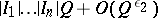 , where
, where 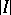 is the length of the interval
is the length of the interval 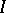 and
and 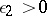 is arbitrary. The validity of inequality (3) for all integers
is arbitrary. The validity of inequality (3) for all integers 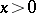 is equivalent to the validity of the inequality
is equivalent to the validity of the inequality
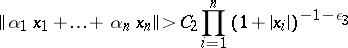 | (4) |
for all integers 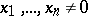 for any
for any 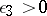 , where
, where 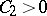 depends only on
depends only on  and
and 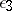 .
.
The proof of the solvability or non-solvability of Diophantine inequalities whose parameters are determined by arithmetical or analytical conditions is often a very complex task. Thus, the problem of approximating algebraic numbers by rational numbers, which has been systematically studied ever since the Liouville inequality was demonstrated in 1844 (cf. Liouville number), has not yet been conclusively solved (cf. Thue–Siegel–Roth theorem; Diophantine approximation, problems of effective). It has been shown [11] that for algebraic numbers  which are together with 1 linearly independent over the field of rational numbers, the inequalities (3) and (4) are valid for any
which are together with 1 linearly independent over the field of rational numbers, the inequalities (3) and (4) are valid for any 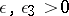 . It follows that the system of inequalities (1) for any
. It follows that the system of inequalities (1) for any 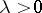 and the system of inequalities (2) for any
and the system of inequalities (2) for any 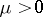 have only a finite number of solutions. There is a close connection between such theorems and Diophantine approximations to algebraic numbers and the representation of integers by incomplete norm forms. In particular, the problem of bounds for the solutions
have only a finite number of solutions. There is a close connection between such theorems and Diophantine approximations to algebraic numbers and the representation of integers by incomplete norm forms. In particular, the problem of bounds for the solutions 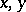 of Thue's Diophantine equation
of Thue's Diophantine equation  , for a given integral irreducible binary form
, for a given integral irreducible binary form 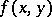 of degree at least three and a variable integer
of degree at least three and a variable integer 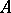 , is equivalent to the study of rational approximations to a root
, is equivalent to the study of rational approximations to a root 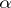 of the polynomial
of the polynomial 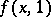 . In this way A. Thue showed that the number of solutions of the equation
. In this way A. Thue showed that the number of solutions of the equation 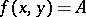 is finite, having previously obtained a non-trivial estimate for rational approximations to
is finite, having previously obtained a non-trivial estimate for rational approximations to 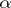 . This approach, generalized and developed by C. Siegel, led him to the theorem that the number of integral points on algebraic curves of genus higher than zero is finite (cf. Diophantine geometry). W. Schmidt [11] used such ideas to obtain a complete solution of the problem of representing numbers by norm forms, basing himself on his approximation theorem. In certain cases the connections between the theory of Diophantine equations and that of Diophantine approximations of numbers may play a main role in proofs on the existence of solutions (in the Waring problem and in the method of Hardy–Littlewood–Vinogradov).
. This approach, generalized and developed by C. Siegel, led him to the theorem that the number of integral points on algebraic curves of genus higher than zero is finite (cf. Diophantine geometry). W. Schmidt [11] used such ideas to obtain a complete solution of the problem of representing numbers by norm forms, basing himself on his approximation theorem. In certain cases the connections between the theory of Diophantine equations and that of Diophantine approximations of numbers may play a main role in proofs on the existence of solutions (in the Waring problem and in the method of Hardy–Littlewood–Vinogradov).
Diophantine approximations to special numbers, given as the values of transcendental functions at rational or algebraic points, are studied by methods of the theory of transcendental numbers (cf. Transcendental number). As a rule, if it can be proved that some number is irrational or transcendental, it is also possible to estimate its approximation by rational or algebraic numbers. In the case of a transcendental 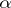 , the magnitude
, the magnitude 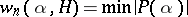 , where the minimum is taken over all non-zero integer polynomials of degree at most
, where the minimum is taken over all non-zero integer polynomials of degree at most  and height at most
and height at most 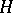 , is called the measure of transcendency of the number
, is called the measure of transcendency of the number 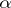 . An estimate from below of
. An estimate from below of 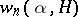 , mainly for a fixed
, mainly for a fixed  and a variable
and a variable 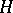 , forms the subject of many theorems in transcendental number theory [12]. For instance, it has been shown by K. Mahler [7], [12] that
, forms the subject of many theorems in transcendental number theory [12]. For instance, it has been shown by K. Mahler [7], [12] that
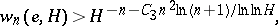 |
where 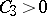 is an absolute constant and
is an absolute constant and 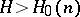 . A. Baker [3] used another method to demonstrate (4) for various non-zero rational powers of
. A. Baker [3] used another method to demonstrate (4) for various non-zero rational powers of  with
with 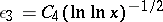 , where
, where
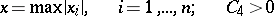 |
depends only on 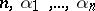 . Since the magnitude
. Since the magnitude 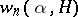 will be "smaller" only if at least one algebraic number of degree at most
will be "smaller" only if at least one algebraic number of degree at most  and height at most
and height at most 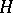 is "close" to
is "close" to 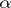 , it follows that there is a connection between the estimation of
, it follows that there is a connection between the estimation of 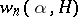 and the estimation of the approximation to
and the estimation of the approximation to 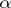 by algebraic numbers of degree at most
by algebraic numbers of degree at most  . Let
. Let 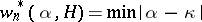 , where the minimum is taken over all algebraic numbers
, where the minimum is taken over all algebraic numbers 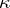 of degree at most
of degree at most  and height at most
and height at most 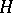 , and let
, and let
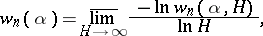 |
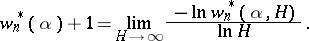 |
E. Wirsing [13] found relations between 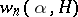 and
and 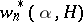 if
if 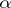 is a real number:
is a real number:
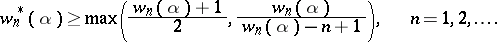 |
In particular, if  , then
, then 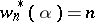 , and since
, and since 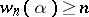 for all transcendental
for all transcendental 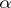 , it follows that
, it follows that 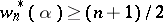 . This means that for any transcendental
. This means that for any transcendental 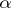 there exists an infinite number of algebraic
there exists an infinite number of algebraic  's of degree at most
's of degree at most  satisfying the inequality
satisfying the inequality
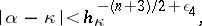 |
where 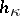 is the height of
is the height of 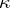 , and
, and 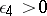 is arbitrary. Wirsing conjectured that
is arbitrary. Wirsing conjectured that  for all transcendental
for all transcendental 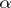 and all
and all 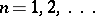 . In addition to the self-evident case
. In addition to the self-evident case 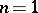 , this conjecture has been demonstrated for
, this conjecture has been demonstrated for 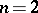 [4]. It is also known that for almost-all (in the sense of Lebesgue measure) real
[4]. It is also known that for almost-all (in the sense of Lebesgue measure) real 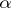 the following equalities are valid:
the following equalities are valid:
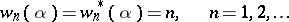 |
(see [2]; Metric theory of numbers; Diophantine approximation, metric theory of).
The study of Diophantine equations by methods of 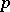 -adic analysis stimulated the development of the theory of Diophantine approximations in the
-adic analysis stimulated the development of the theory of Diophantine approximations in the 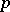 -adic number fields
-adic number fields 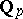 , the structure of which is parallel in many respects to the theory of Diophantine approximations in the field of real numbers, but taking into account the non-Archimedean topology of
, the structure of which is parallel in many respects to the theory of Diophantine approximations in the field of real numbers, but taking into account the non-Archimedean topology of 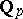 . For instance, let
. For instance, let 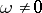 be a
be a 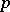 -adic number. A consideration of approximations of zero (in the
-adic number. A consideration of approximations of zero (in the 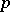 -adic metric) by the values of the integral linear form
-adic metric) by the values of the integral linear form 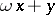 yields rational approximations of
yields rational approximations of 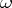 which, as in the case of real numbers, are closely connected with the expansion of
which, as in the case of real numbers, are closely connected with the expansion of 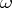 into a continued (
into a continued (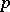 -adic) fraction [10]. Analogues of the theorems of Dirichlet, Kronecker, Minkowski, etc., metric theorems, theorems on approximations by algebraic numbers, etc., are all valid [2], [6], [8]. Diophantine inequalities in
-adic) fraction [10]. Analogues of the theorems of Dirichlet, Kronecker, Minkowski, etc., metric theorems, theorems on approximations by algebraic numbers, etc., are all valid [2], [6], [8]. Diophantine inequalities in 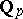 may be interpreted as congruences by a "high" degree of
may be interpreted as congruences by a "high" degree of 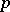 , which makes it possible to obtain pure arithmetical theorems by an analytic method. A far-going development of Diophantine approximations in the field
, which makes it possible to obtain pure arithmetical theorems by an analytic method. A far-going development of Diophantine approximations in the field 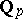 and its finite extensions makes it possible to use the Thue–Siegel–Roth method to demonstrate theorems on the arithmetical structure of numbers representable by binary forms, on estimates of the fractional parts of powers of rational numbers, etc. [10].
and its finite extensions makes it possible to use the Thue–Siegel–Roth method to demonstrate theorems on the arithmetical structure of numbers representable by binary forms, on estimates of the fractional parts of powers of rational numbers, etc. [10].
Since the expansion of functions into continued fractions is similar to the expansion of numbers into continued fractions, a further analogy arises naturally — approximations of a function by rational functions in the metric of a field of power series. This approach has been considerably developed and leads to the theory of Diophantine approximations in a field of power series. Let 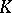 be an arbitrary algebraic field, let
be an arbitrary algebraic field, let 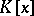 be the ring of polynomials in
be the ring of polynomials in  over
over 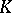 and let
and let 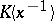 be the field of power series of the form
be the field of power series of the form
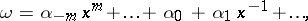 |
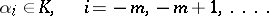 |
One introduces a non-Archimedean valuation,
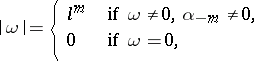 |
where 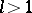 is an arbitrary fixed number, in the field
is an arbitrary fixed number, in the field 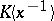 . The field
. The field 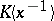 with the norm
with the norm 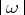 becomes a metric space. The study of "Diophantine" approximations is carried out in the usual way, with
becomes a metric space. The study of "Diophantine" approximations is carried out in the usual way, with 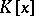 acting as the ring of integers: The approximating functions under consideration are functions, with values in
acting as the ring of integers: The approximating functions under consideration are functions, with values in 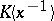 , of a finite number of variables with values in
, of a finite number of variables with values in 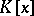 , while the estimation is carried out with respect to the norm introduced. There is a certain similarity between results obtained in this manner and the case of Diophantine approximations in the field of real numbers, but if
, while the estimation is carried out with respect to the norm introduced. There is a certain similarity between results obtained in this manner and the case of Diophantine approximations in the field of real numbers, but if 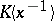 is replaced by the field
is replaced by the field 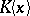 of series of the form
of series of the form
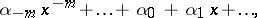 |
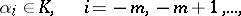 |
the results are analogous to approximations in a 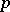 -adic number field [2], [9].
-adic number field [2], [9].
Diophantine approximations in a field of power series form a more concrete basis of certain analytic methods in the theory of transcendental numbers (specialization of 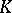 , explicit estimation of the accuracy of approximation, etc.).
, explicit estimation of the accuracy of approximation, etc.).
Three different approaches in the development of the theory of Diophantine approximations may be distinguished: global, metric and individual. The global approach involves the study of general laws of approximation, which apply to all numbers or to all numbers with "rare" exceptions. This is the case of the Dirichlet theorem on homogeneous approximations, Kronecker's theorem on inhomogeneous approximations, general theorems on the approximation of numbers by algebraic numbers, classifications of numbers by their approximation properties, etc. The corresponding methods are "global" (continued fractions, etc.). The metric approach involves the description of the approximation properties of numbers on the base of concepts of measure theory (cf. Diophantine approximation, metric theory of; Metric theory of numbers). The results thus obtained do not apply to all, but to almost-all (in the sense of a definite measure) numbers in the sets under consideration or else are described with the aid of some metric characteristic (the Hausdorff dimension, the capacity, etc.). The methods used are closely connected with measure theory, probability theory and related disciplines. The individual approach concerns the approximation properties of special numbers (algebraic numbers,  ,
, 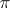 ,
, 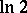 , etc.) or else involves the construction of numbers with specified approximation properties (Liouville numbers, Mahler
, etc.) or else involves the construction of numbers with specified approximation properties (Liouville numbers, Mahler 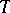 -numbers, etc.). The methods for solving such problems are specific and are often specially developed for a specific problem.
-numbers, etc.). The methods for solving such problems are specific and are often specially developed for a specific problem.
References
| [1] | J.W.S. Cassels, "An introduction to diophantine approximation" , Cambridge Univ. Press (1957) MR0087708 Zbl 0077.04801 |
| [2] | V.G. Sprindzhuk, "Mahler's problem in metric number theory" , Amer. Math. Soc. (1969) (Translated from Russian) |
| [3] | A. Baker, "On some Diophantine inequalities involving the exponential function" Canad. J. Math. , 17 (1965) pp. 616–626 MR0177946 Zbl 0147.30901 |
| [4] | H. Davenport, W. Schmidt, "Approximation to real numbers by quadratic irrationals" Acta Arithm. , 13 (1967) pp. 169–176 MR0219476 Zbl 0155.09503 |
| [5] | J.F. Koksma, "Diophantische Approximationen" , Springer (1936) MR0344200 MR0004857 MR1545368 Zbl 0012.39602 Zbl 62.0173.01 |
| [6] | E. Lutz, "Sur les approximations diophantiennes linéaires 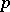 -adiques" , Hermann (1955) MR69224 -adiques" , Hermann (1955) MR69224 |
| [7] | K. Mahler, "Ueber Beziehungen zwischen der Zahl $e$ und Liouvilleschen Zahlen" Math. Z. , 31 (1930) pp. 729–732 |
| [8] | K. Mahler, "Ueber Diophantische Approximationen im Gebiete der 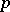 -adischen Zahlen" Jahresber. Deutsch. Math-Verein. , 44 (1934) pp. 250–255 -adischen Zahlen" Jahresber. Deutsch. Math-Verein. , 44 (1934) pp. 250–255 |
| [9] | K. Mahler, "An analogue of Minkowski's theory of numbers in a field of series" Ann. of Math , 42 (1941) pp. 488–522 |
| [10] | K. Mahler, "Lectures on Diophantine approximations" , 1 , Univ. Notre Dame (1961) MR0142509 Zbl 0158.29903 |
| [11] | W. Schmidt, "Approximation to algebraic numbers" Enseign. Math. (2) , 17 : 3–4 (1971) pp. 187–253 MR0327672 Zbl 0226.10033 Zbl 0217.03902 |
| [12] | T. Schneider, "Einführung in die transzendenten Zahlen" , Springer (1957) MR0086842 Zbl 0077.04703 |
| [13] | E. Wirsing, "Approximation mit algebraischen Zahlen beschränkten Grades" J. Reine Angew. Math. , 206 : 1–2 (1961) pp. 67–77 MR0142510 Zbl 0097.03503 |
Comments
The most important developments in Diophantine approximations are in the direction of transcendental number theory, irrational number theory and distribution modulo one.
Concerning the problem of representing numbers by norm forms one has the following, [a2]. Let 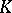 be an algebraic number field and let
be an algebraic number field and let 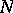 denote the norm map
denote the norm map 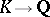 . Let
. Let 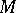 be a module in
be a module in  , i.e., a finite dimensional
, i.e., a finite dimensional 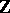 -module
-module 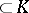 (also called an (incomplete) lattice). One speaks of a full module if
(also called an (incomplete) lattice). One speaks of a full module if  . Then a necessary and sufficient condition for there to exist an integer
. Then a necessary and sufficient condition for there to exist an integer 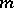 such that the equation
such that the equation 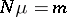 has infinitely many solutions
has infinitely many solutions 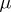 in
in 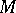 is that
is that  be a full module in some subfield of
be a full module in some subfield of  that is neither the rational nor an imaginary quadratic field.
that is neither the rational nor an imaginary quadratic field.
Let 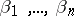 be a basis for a module
be a basis for a module 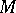 . Consider the linear form
. Consider the linear form 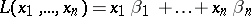 . Let
. Let 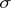 run through the imbeddings of
run through the imbeddings of 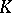 into the complex numbers
into the complex numbers 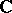 . Let
. Let 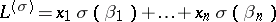 . The product
. The product 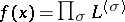 is a homogeneous form of degree
is a homogeneous form of degree  over
over 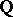 . Such forms are called norm forms, and solving
. Such forms are called norm forms, and solving 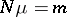 is of course the same as representing
is of course the same as representing 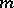 by the form
by the form 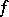 (with entries from
(with entries from 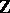 ).
).
References
| [a1] | A. Baker, "Transcendental number theory" , Cambridge Univ. Press (1975) MR0422171 Zbl 0297.10013 |
| [a2] | W.M. Schmidt, "Linearformen. II" Math. Ann. , 191 (1971) pp. 1–20 MR0308062 |
| [a3] | W.M. Schmidt, "Diophantine Approximation" , Lect. notes in math. , 785 , Springer (1980) MR0568710 Zbl 0421.10019 |
Diophantine approximations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Diophantine_approximations&oldid=40755