Differential equation, partial, free boundaries
The problem of finding the solution of a system of partial differential equations with suitable initial and boundary conditions in a domain whose boundary is completely, or partially, unknown and must be determined. Problems of this type arise in many problems of filtration, diffusion, thermal conduction, and other branches of the mechanics of continuous media. For instance, the Helmholtz–Kirchhoff problem on symmetrical current flow around an equilateral wedge with an apex angle of $ 2 \alpha \pi $
of an unbounded flux of an ideal liquid consists in finding the velocity components $ u = u ( x , y ) $,
$ v = v ( x , y ) $,
which are the solution of the Cauchy–Riemann system of equations:
$$ \frac{\partial u }{\partial x } + \frac{\partial v }{\partial y } = 0 ,\ \ \frac{\partial u }{\partial y } - \frac{\partial v }{\partial x } = 0 , $$
and which satisfy, on a certain boundary, the conditions (see Fig.):
$$ \left . v \right | _ {A O } = 0 ,\ \left . v \right | _ {O B } = \left . \mathop{\rm tan} \alpha \pi u \right | _ {O B } . $$
The unknown boundary $ BS $ is a stream line on which the supplementary condition
$$ u ^ {2} + v ^ {2} = v _ \infty ^ {2} ,\ \lim\limits _ {r \rightarrow \infty } u = v _ \infty ,\ r = \sqrt {x ^ {2} + y ^ {2} } , $$
has been imposed. The figure shows the upper half of the stream, $ y \geq 0 $; for $ y \leq 0 $ the stream is symmetric.
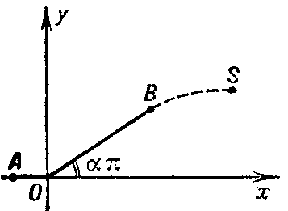
Figure: d031980a
In solving problems with a free boundary in the plane, extensive use is made of methods of the theory of functions of a complex variable.
See also Stefan problem.
References
| [1] | V.N. Monakhov, "Boundary-value problems with free boundaries for elliptic systems of equations" , Amer. Math. Soc. (1983) (Translated from Russian) MR0717387 Zbl 0532.35001 |
| [2] | A. Fasano (ed.) M. Primicerio (ed.) , Free boundary problems: theory and application , 1–2 , Pitman (1983) MR0714899 |
| [3] | I.I. Danilyuk, "On the Stefan problem" Russian Math. Surveys , 40 : 5 (1985) pp. 157–223 Uspekhi Mat. Nauk , 40 : 5 (245) (1985) pp. 133–185 MR810813 Zbl 0604.35080 |
Comments
Free boundary problems for partial differential equations are frequently encountered in a variety of applications. Besides the classical free boundary problems in fluid dynamics (e.g., jets and cavities), in filtration theory (e.g. the displacement of immiscible fluids in porous media, also known as Muskat's or Verigin's problem), in change of phase (Stefan problem), in crystal growth, and in linear elasticity (e.g. the obstacle problem), many other interesting problems can be listed. For instance, free boundaries can arise in the motion of non-Newtonian fluids (A.E. Bingham), in non-linear diffusion with degeneracy (i.e. diffusion governed by the so-called porous medium equation), in reaction-diffusion systems, etc. A common feature of free boundary problems is the necessity of extra conditions on the free boundary. Such conditions involve the unknown function $ u $ in the partial differential equation and/or its derivatives up to an order which can even exceed the order of the differential equation. They may or may not involve the normal component of the velocity of the free boundary. Sometimes they have a non-local character, being expressed in terms of functionals acting on $ u $ and on the free boundary itself. From the mathematical point of view the occurrence of a free boundary can be frequently related to discontinuities or even singularities of some of the coefficients of the differential equation in correspondence of some given value $ u _ {0} $ of $ u $. In studying a free boundary problem of the latter type one can follow the classical approach, trying to determine the free boundary and a regular solution $ u $ of the partial differential equation, or one can consider a generalized (or weak) formulation in which the free boundary is defined implicitly as the set $ \{ u = u _ {0} \} $, requiring $ u $ to belong to some Sobolev space. However in such a case it is generally very hard to retrieve any information on the regularity of the free boundary.
See also Differential equation, partial, discontinuous coefficients; Differential equation, partial, with singular coefficients.
References
| [a1] | D.A. Tarzia, "A bibliography on moving-free boundary problems for the heat-diffusion equation" , Prog. Naz. "Equazioni di evoluzione e applicazioni fisico-matematiche" , Firenze (1988) MR1007840 Zbl 0694.35221 |
| [a2] | J. Crank, "Free and moving boundary problems" , Clarendon Press (1984) MR0776227 MR0891186 Zbl 0547.35001 |
| [a3] | C.M. Elliot, J.R. Ockendon, "Weak and variational methods for moving boundary problems" , Pitman (1982) MR650455 |
| [a4] | A.M. Meirmanov, "Stefan problem" , Novosibirsk (1986) (In Russian) MR0945824 MR0839191 Zbl 0909.35156 Zbl 0866.35141 Zbl 0812.35165 Zbl 0833.35155 Zbl 0788.35153 Zbl 0751.35052 Zbl 0593.35093 Zbl 0619.35054 |
| [a5] | L.I. Rubinstein, "The Stefan problem" , Amer. Math. Soc. (1971) (Translated from Russian) MR0351348 Zbl 0952.35162 Zbl 0866.35146 Zbl 0488.35012 Zbl 0491.35084 Zbl 0456.35096 Zbl 0434.35086 |
| [a6] | J.I. Diaz, "Nonlinear partial differential equations and free boundaries" , 1. Elliptic equations , Pitman (1985) MR0853732 Zbl 0595.35100 |
| [a7] | A. Friedman, "Variational principles and free-boundary problems" , Wiley (1982) MR0679313 Zbl 0564.49002 |
| [a8] | J.F. Rodrigues, "Obstacle problems in mathematical physics" , North-Holland (1987) MR0880369 Zbl 0606.73017 |
| [a9] | A. Fasano (ed.) M. Primicerio (ed.) , Nonlinear diffusion problems , Lect. notes in math. , 1224 , Springer (1986) MR0877985 Zbl 0595.00014 |
| [a10] | A. Bossavit (ed.) A. Damlamian (ed.) M. Frémond (ed.) , Free boundary problems: applications and theory , 3–4 , Pitman (1985) MR0903283 MR0863154 Zbl 0578.35003 |
| [a11] | J. Albrecht (ed.) L. Collatz (ed.) K.H. Hofmann (ed.) , Numerical treatment of free boundary value problems , Birkhäuser (1982) MR0680238 Zbl 0469.00014 |
Differential equation, partial, free boundaries. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_equation,_partial,_free_boundaries&oldid=46673