Cusp(2)
cuspidal point
A singular point of a curve, the two branches of which have a common semi-tangent there. In the case of a plane curve one distinguishes cusps of the first and the second kind. In the former case the curve lies on one side of the tangent cone (Fig.a); in the second, on different sides (Fig.b).
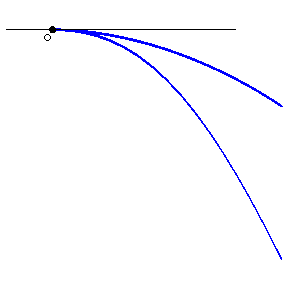
Figure: c027420a
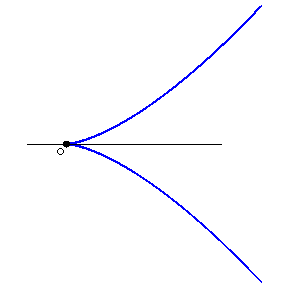
Figure: c027420b
Comments
In the above the word "branch" is used in a naive and non-technical sense as follows. View a curve $C$ as the image of a finite or infinite interval in Euclidean space $E^n$. Let $\phi$ be a single-valued analytic function defined on some interval. If $x=\phi(y)$ (or $y=\phi(x)$) defines a subset $C_0$ of $C$, one speaks of a branch of $C$. Here $n=2$ is taken for convenience. There is a second more technical (and more precise) notion of a branch in algebraic and analytic geometry which defines the branches at a point $x\in C$ as the points above $x$ on the normalization of the curve $C$ (cf. Normal scheme). Using this concept a cusp is a singular point of a curve which has only one branch at this point.
A curve with a cusp of the first kind (Fig.a) is, e.g., $X^4+X^2Y^2+2X^2Y-XY^2+Y^2=0$, and one with a cusp of the second kind (Fig.b) — e.g. $Y^2=X^3$.
The word "cusp" is also used in the theory of modular forms (see Fuchsian group; Modular form).
References
| [a1] | R.J. Walker, "Algebraic curves" , Springer (1978) |
Cusp(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cusp(2)&oldid=53403