Cooperative game
A non-strategic game (see Games, theory of), defined by a triple  , where
, where  is a (usually finite) set whose elements are called players, the subsets
is a (usually finite) set whose elements are called players, the subsets  are called coalitions,
are called coalitions,  is a real-valued function defined on the set of coalitions, called the characteristic function of the game, and
is a real-valued function defined on the set of coalitions, called the characteristic function of the game, and  is a subset of vectors
is a subset of vectors  (the components
(the components  correspond to player
correspond to player  in
in  ) called the imputations. Cooperative games were first introduced by J. von Neumann, 1928, as a tool in the cooperative theory of (non-cooperative) games.
) called the imputations. Cooperative games were first introduced by J. von Neumann, 1928, as a tool in the cooperative theory of (non-cooperative) games.
In the classical theory of cooperative games one takes:
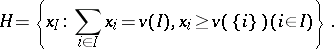 |
On the set 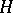 one introduces the binary relation
one introduces the binary relation 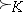 of dominance (preference) of the imputations with respect to the coalition
of dominance (preference) of the imputations with respect to the coalition 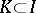 :
:
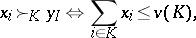 |
 |
If  for some
for some  , then one writes
, then one writes  . Notions of optimality of an imputation are formulated in terms of this relation of dominance.
. Notions of optimality of an imputation are formulated in terms of this relation of dominance.
A significant part of the contents of the theory of cooperative games consists of elaborating the notions of optimality, of proving their realizability for various special classes of cooperative games, and of actually discovering such realizations. Among the principles of optimality that have been developed in connection with cooperative games are the following: double (namely, internal and external) stability, realizable in the form of von Neumann–Morgenstern solutions (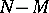 -solutions, cf. Solution in game theory); undominated imputations (see Core in the theory of games); stability with respect to threats; stability in the sense of minimization of the greatest insufficiency (see Stability in game theory); fairness (see Shapley vector); etc.
-solutions, cf. Solution in game theory); undominated imputations (see Core in the theory of games); stability with respect to threats; stability in the sense of minimization of the greatest insufficiency (see Stability in game theory); fairness (see Shapley vector); etc.
The introduction of algebraic operations in the class of cooperative games leads to the calculus of cooperative games and to the investigation of interrelations between these operations and various principles of optimality. The different special classes of cooperative games described below have been given special attention.
A simple game is a cooperative game in which the characteristic function  takes exactly two values (usually 0 and 1); here, coalitions
takes exactly two values (usually 0 and 1); here, coalitions 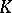 on which the maximum value of
on which the maximum value of 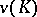 is attained are called winning. A special case of simple games is a weighted majority game, in which a coalition
is attained are called winning. A special case of simple games is a weighted majority game, in which a coalition 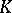 is winning if
is winning if  , where
, where  (
(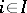 ) and
) and 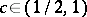 are certain constants.
are certain constants.
A balanced game is a cooperative game whose characteristic function is such that
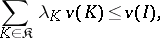 |
if the family of coalitions 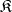 and the non-negative numbers
and the non-negative numbers 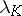 (
(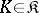 ) are such that
) are such that
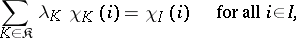 |
where 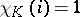 if
if 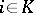 and 0 otherwise. Balanced games and only they have a non-empty
and 0 otherwise. Balanced games and only they have a non-empty  -core (cf. Core in the theory of games).
-core (cf. Core in the theory of games).
A convex game is a cooperative game whose characteristic function is such that for  ,
,
 | (*) |
In a convex game the  -core is non-empty and coincides with the
-core is non-empty and coincides with the  -solutions. If a cooperative game is strictly convex (that is, the inequality (*) is strict), then the Shapley vector (value) is the centre of gravity of the
-solutions. If a cooperative game is strictly convex (that is, the inequality (*) is strict), then the Shapley vector (value) is the centre of gravity of the  -core.
-core.
A quota-game is a cooperative game with characteristic function  for which there exists a vector
for which there exists a vector 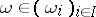 such that
such that  and
and  for any two players
for any two players 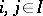 (
( ).
).
A market game is a cooperative game induced by a market, which is taken to be a system
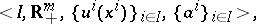 |
where 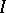 is the set of participants in the market (with
is the set of participants in the market (with 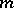 commodities),
commodities), 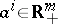 is the initial bundle of commodities of the
is the initial bundle of commodities of the  -th participant and
-th participant and  is the utility function of the
is the utility function of the 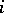 -th participant defined on
-th participant defined on 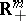 . On the basis of such a market a cooperative game is constructed in which
. On the basis of such a market a cooperative game is constructed in which
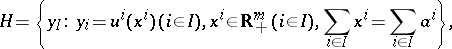 |
while the characteristic function is defined by
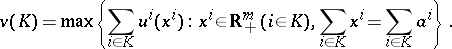 |
The theory of classical cooperative games has undergone generalizations in various directions (see also Non-atomic game).
Games without side payments are non-strategic games defined by a triple 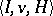 , where
, where  (in contrast to classical cooperative games) is a function that associates with each coalition
(in contrast to classical cooperative games) is a function that associates with each coalition  a set
a set 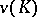 of vectors
of vectors 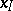 satisfying the following conditions: 1)
satisfying the following conditions: 1) 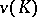 is closed and convex; 2) if
is closed and convex; 2) if  and
and 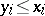 (
( ), then
), then 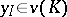 ; 3) if
; 3) if  , then
, then 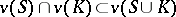 ; 4)
; 4) 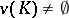 for all
for all  ; and 5)
; and 5)  if and only if
if and only if 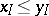 for some
for some 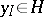 .
.
Dominance in a game without side payments is defined as follows:  if there exists a non-empty coalition
if there exists a non-empty coalition 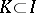 such that
such that
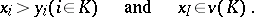 |
A game in partition function form is a non-strategic game defined by a set of players 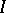 and a function
and a function  that associates with each partition
that associates with each partition 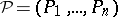 of the set
of the set  a vector
a vector  . The maximal pay-off that the coalition
. The maximal pay-off that the coalition 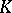 itself can guarantee is defined by the formula
itself can guarantee is defined by the formula 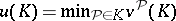 . An imputation in a game in partition function form is defined as a vector
. An imputation in a game in partition function form is defined as a vector 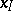 satisfying the conditions:
satisfying the conditions: 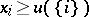 (
(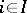 );
); 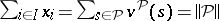 for some
for some 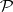 . An imputation
. An imputation 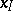 dominates an imputation
dominates an imputation 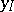 with respect to a coalition
with respect to a coalition 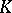 if: 1)
if: 1) 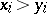 (
(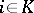 ); 2)
); 2) 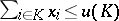 ; and 3) there exists a
; and 3) there exists a 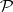 such that
such that 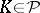 and
and  .
.
References
| [1] | J. von Neumann, O. Morgenstern, "Theory of games and economic behavior" , Princeton Univ. Press (1953) |
| [2] | N.N. Vorob'ev, "The present state of the theory of games" Russian Math. Surveys , 25 : 2 (1970) pp. 81–140 Uspekhi Mat. Nauk , 25 : 2 (1970) pp. 103–107 |
| [3] | I. Rosenmüller, "The theory of games and markets" , North-Holland (1981) (Translated from German) |
Comments
References
| [a1] | J.W. Friedman, "Oligopoly and the theory of games" , North-Holland (1977) |
| [a2] | J. Szép, F. Forgó, "Introduction to the theory of games" , Reidel (1985) |
Cooperative game. N.N. Vorob'evA.I. Sobolev (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cooperative_game&oldid=14003