Convex functional
A functional, defined on a convex subset of a linear vector space, the supergraph of which is a convex set. A functional 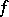 which does not assume the value
which does not assume the value 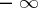 on a convex set
on a convex set 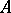 is convex on
is convex on 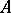 if and only if the inequality
if and only if the inequality
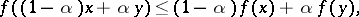 |
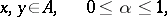 |
is satisfied. If the inequality sign is reversed, the functional 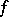 is called concave. Operations which convert a convex functional into a convex functional include addition
is called concave. Operations which convert a convex functional into a convex functional include addition 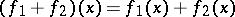 , multiplication by a positive number, taking the upper bound
, multiplication by a positive number, taking the upper bound
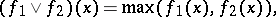 |
and the infimal convolution
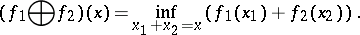 |
A convex functional bounded from above in a neighbourhood of some point  is continuous at that point. If a convex functional is finite at some point
is continuous at that point. If a convex functional is finite at some point  , it has a (finite or infinite) derivative in any direction at that point. Closed convex functionals (i.e. functionals with convex and closed supergraphs) in locally convex linear topological spaces may be described in a dual way: Such a functional is the least upper bound of the affine functions which it dominates. This duality makes it possible to relate to each convex functional a dual object, the conjugate functional
, it has a (finite or infinite) derivative in any direction at that point. Closed convex functionals (i.e. functionals with convex and closed supergraphs) in locally convex linear topological spaces may be described in a dual way: Such a functional is the least upper bound of the affine functions which it dominates. This duality makes it possible to relate to each convex functional a dual object, the conjugate functional
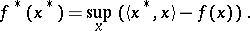 |
Properties of convex functionals, operations on such functionals, and the relationship between a convex functional and its conjugate, are studied in convex analysis.
References
| [1] | Z.W. Birnbaum, W. Orlicz, "Ueber die Verallgemeinerung des Begriffes der zueinander konjugierter Potenzen" Studia Math. , 3 (1931) pp. 1–67 |
| [2] | G.H. Hardy, J.E. Littlewood, G. Pólya, "Inequalities" , Cambridge Univ. Press (1934) MR2591337 MR1601748 MR1472649 MR1478445 MR1234454 MR1146141 MR1136994 MR0944909 MR0197653 MR0046395 MR0083530 MR0008854 MR1563622 MR1545539 MR1545530 Zbl 0010.10703 Zbl 60.0169.01 |
| [3] | M.A. Krasnosel'skii, Ya.B. Rutitskii, "Convex functions and Orlicz spaces" , Noordhoff (1961) (Translated from Russian) Zbl 0095.09103 |
| [4] | W. Fenchel, "On conjugate convex functions" Canad. J. Math. , 1 (1949) pp. 73–77 MR0028365 Zbl 0038.20902 |
| [5] | R.T. Rockafellar, "Convex analysis" , Princeton Univ. Press (1970) MR0274683 Zbl 0193.18401 |
Convex functional. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convex_functional&oldid=28163