Continuous operator
A continuous mapping 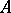 of a subset
of a subset 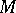 of a topological space
of a topological space 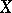 , which as a role is also a vector space, into a space
, which as a role is also a vector space, into a space 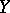 of the same type, specifically: A mapping
of the same type, specifically: A mapping 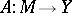 ,
, 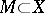 , is continuous at a point
, is continuous at a point 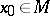 if for any neighbourhood
if for any neighbourhood 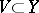 of the point
of the point 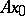 there is a neighbourhood
there is a neighbourhood 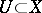 of
of 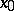 such that
such that 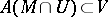 ; a mapping
; a mapping 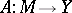 is continuous on a set
is continuous on a set 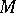 if it is continuous at every point of
if it is continuous at every point of 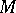 .
.
For an operator 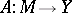 to be continuous on
to be continuous on 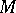 it is necessary and sufficient that for every open (closed) set
it is necessary and sufficient that for every open (closed) set 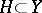 the complete inverse image
the complete inverse image 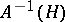 is the trace on
is the trace on 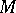 of an open (closed) set in
of an open (closed) set in 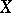 , that is,
, that is, 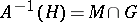 , where
, where 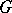 is open (closed) in
is open (closed) in  . For continuous operators the chain rule holds: Suppose that
. For continuous operators the chain rule holds: Suppose that  ,
,  , is continuous on
, is continuous on 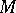 (or at
(or at 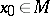 ) and suppose also that
) and suppose also that 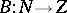 ,
, 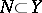 , is continuous on
, is continuous on 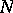 (or at
(or at 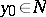 ). If
). If 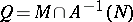 is not empty (or
is not empty (or  ), then
), then  is continuous on
is continuous on 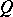 (or at
(or at 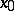 ).
).
When 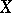 and
and 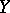 are topological vector spaces and
are topological vector spaces and 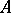 is a linear continuous operator on a linear subspace
is a linear continuous operator on a linear subspace 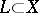 with values in
with values in 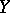 , then the continuity of
, then the continuity of 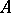 at some point of
at some point of 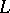 , say, at the origin, implies the continuity of
, say, at the origin, implies the continuity of 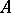 on the whole of
on the whole of 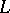 . A continuous operator on a submanifold
. A continuous operator on a submanifold  of a topological vector space
of a topological vector space  is bounded on
is bounded on 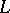 , that is, the image of any bounded set
, that is, the image of any bounded set 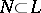 is bounded in
is bounded in 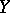 . If
. If 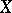 and
and 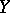 are separable, then the compactness of
are separable, then the compactness of 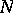 implies that of
implies that of 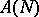 .
.
An operator 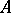 is uniformly continuous on
is uniformly continuous on 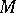 if for any neighbourhood of the origin
if for any neighbourhood of the origin  there exists a neighbourhood of the origin
there exists a neighbourhood of the origin 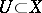 such that
such that 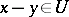 implies
implies 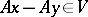 . An operator that is linear and continuous on a linear submanifold of a topological vector space is automatically uniformly continuous on this submanifold.
. An operator that is linear and continuous on a linear submanifold of a topological vector space is automatically uniformly continuous on this submanifold.
Apart from continuity one introduces the concept of countable continuity of an operator. An operator 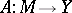 is countably continuous at
is countably continuous at 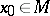 if
if 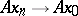 for any sequence
for any sequence 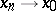 ,
, 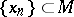 . For metrizable spaces continuity and countable continuity coincide.
. For metrizable spaces continuity and countable continuity coincide.
References
| [1] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [2] | L.V. Kantorovich, G.P. Akilov, "Functional analysis in normed spaces" , Pergamon (1974) (Translated from Russian) |
Comments
In Western literature the term "operatoroperator" tends to be reserved for a mapping between vector spaces. See [a1], [a2].
References
| [a1] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) |
| [a2] | A.E. Taylor, D.C. Lay, "Introduction to functional analysis" , Wiley (1980) |
Continuous operator. V.I. Sobolev (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Continuous_operator&oldid=14154