Continuation method (to a parametrized family, for non-linear operators)
A method for approximately solving non-linear operator equations. It consists of generalizing the equation to be solved, 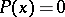 , to the form
, to the form  , by introducing a parameter
, by introducing a parameter 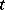 that takes values in a finite interval,
that takes values in a finite interval, 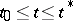 , such that the initial equation is obtained for
, such that the initial equation is obtained for 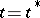 :
: 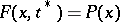 , while the equation
, while the equation 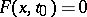 can either easily be solved, or a solution
can either easily be solved, or a solution 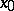 of it is already known (cf. [1]–[3]).
of it is already known (cf. [1]–[3]).
The generalized equation 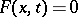 is solved sequentially for individual values of
is solved sequentially for individual values of 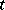 :
: 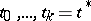 . For
. For 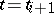 it is solved by means of some iteration method (Newton, simple iteration, variation of parameter, [4], etc.), starting with the solution
it is solved by means of some iteration method (Newton, simple iteration, variation of parameter, [4], etc.), starting with the solution 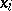 obtained by solving
obtained by solving 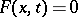 for
for 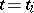 . Applying at each step in
. Applying at each step in 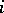 , e.g.,
, e.g.,  Newton iterations, leads to the formulas
Newton iterations, leads to the formulas
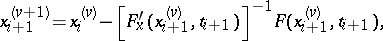 |
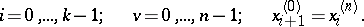 |
If the difference 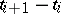 is sufficiently small, then the value of
is sufficiently small, then the value of 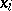 may turn out to be a sufficiently good initial approximation, ensuring convergence, in order to obtain the solution
may turn out to be a sufficiently good initial approximation, ensuring convergence, in order to obtain the solution 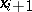 for
for 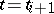 (cf. [1], [3], [5]).
(cf. [1], [3], [5]).
In practice, the initial problem often naturally depends on some parameter, which can then be taken as 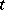 .
.
The continuation method is used in the solution of systems of non-linear algebraic and transcendental equations (cf. [1], [2]), as well as for more general non-linear functional equations in Banach spaces (cf. [5]–[7]).
The continuation method is sometimes called the direct method of variation of parameter (cf. [2], [6]), as well as the combined method of direct and iterative variation of parameter. In these methods the construction of solutions of generalized equations is reduced, by differentiation with respect to the parameter, to the solution of a differential problem with initial conditions (a Cauchy problem) by methods of numerical integration of ordinary differential equations. Applying the simplest Euler method in the direct method of variation of parameter to the Cauchy problem
 |
the approximate values 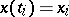 ,
, 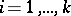 , of the solution
, of the solution 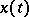 of
of 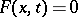 can be determined from the following identities:
can be determined from the following identities:
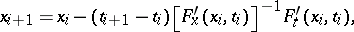 |
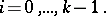 |
The element 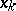 is the required approximate solution of the initial equation
is the required approximate solution of the initial equation 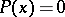 . A refinement of all or some values
. A refinement of all or some values 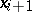 can be obtained by the iteration method of variation of parameter [4] (or Newton's method). The generalized equation is here usually generated in the form
can be obtained by the iteration method of variation of parameter [4] (or Newton's method). The generalized equation is here usually generated in the form
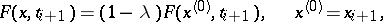 |
on a finite interval 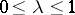 , or, replacing in it
, or, replacing in it 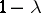 by
by  , on the infinite interval
, on the infinite interval 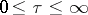 .
.
The method of variation of parameter has been applied to large classes of problems both for constructing solutions, as well as for proving their existence (cf. e.g. [3], [4], [6], [7]).
References
| [1] | E. Lahaye, "Sur la résolution des systèmes d'equations transcendantes" Acad. Roy. Belgique Bull. Cl. Sci. Sér. 5 , 34 (1948) pp. 809–827 |
| [2] | D.F. Davidenko, "On the approximate solution of systems of non-linear equations" Ukrain. Mat. Zh. , 5 : 2 (1953) pp. 196–206 (In Russian) |
| [3] | J.M. Ortega, W.C. Rheinboldt, "Iterative solution of non-linear equations in several variables" , Acad. Press (1970) |
| [4] | D.F. Davidenko, "An iterative method of parameter variation for inverting linear operators" USSR Comput. Math. Math. Phys. , 15 (1975) pp. 27–43 Zh. Vychisl. Mat. i. Mat. Fiz. , 15 : 1 (1975) pp. 30–47 |
| [5] | A.M. Dement'eva, "On difference methods of constructing an implicit function" Soviet Math. Doklady , 12 (1971) pp. 1708–1711 Dokl. Akad. Nauk SSSR , 201 : 4 (1971) pp. 774–777 |
| [6] | D.F. Davidenko, "On applying the method of variation of parameters to the theory of non-linear functional equations" Ukrain. Mat. Zh. , 7 : 1 (1955) pp. 18–28 (In Russian) |
| [7] | N.A. Shidlovskaya, "Application of the method of differentiation with respect to a parameter to the solution of non-linear equations in Banach spaces" Uchen. Zap. Leningrad. Gos. Univ. , 271 : 33 (1958) pp. 3–17 (In Russian) |
Comments
Cf. Continuation method (to a parametrized family) for editorial comments.
Continuation method (to a parametrized family, for non-linear operators). D.F. Davidenko (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Continuation_method_(to_a_parametrized_family,_for_non-linear_operators)&oldid=13519