Contact structure
An infinitesimal structure of order one on a smooth manifold  of odd dimension that is determined by defining on
of odd dimension that is determined by defining on  a
a  -form
-form  for which
for which  . The form
. The form  is then called a contact form on
is then called a contact form on  . A contact structure exists only on an orientable
. A contact structure exists only on an orientable  and defines a unique vector field
and defines a unique vector field  on
on 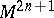 for which
for which 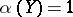 and
and 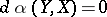 for any vector field
for any vector field  ; the field
; the field 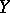 is called the dynamical system on
is called the dynamical system on  corresponding to the contact form
corresponding to the contact form 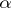 . Contact structures find applications in analytic mechanics due to the fact that on any level submanifold of the Hamiltonian, defined in phase space, there arises a natural contact structure.
. Contact structures find applications in analytic mechanics due to the fact that on any level submanifold of the Hamiltonian, defined in phase space, there arises a natural contact structure.
References
| [1] | C. Godbillon, "Géométrie différentielle et mécanique analytique" , Hermann (1969) |
Comments
More precisely, the notion defined above is a strict contact structure or exact contact structure, [a1], [a2]. Let 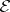 be a Pfaffian equation on
be a Pfaffian equation on  , i.e. a one-dimensional subbundle of the cotangent bundle
, i.e. a one-dimensional subbundle of the cotangent bundle 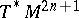 . Let
. Let  be a
be a 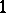 -form (i.e. a Pfaffian form) in a neighbourhood
-form (i.e. a Pfaffian form) in a neighbourhood 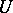 of
of 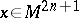 that defines
that defines 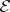 over
over  , i.e.
, i.e. 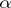 is a section of
is a section of 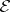 over
over  that is everywhere non-zero on
that is everywhere non-zero on 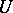 . Then there is an integer
. Then there is an integer  such that
such that 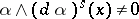 and
and 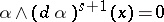 . This does not depend on the choice of
. This does not depend on the choice of 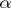 . The odd integer
. The odd integer 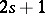 is called the class of the Pfaffian equation
is called the class of the Pfaffian equation 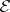 at
at  . A contact structure on
. A contact structure on  is now given by a Pfaffian equation
is now given by a Pfaffian equation 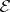 on
on 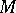 which is everywhere of class
which is everywhere of class 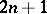 . The pair
. The pair 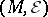 is called a contact manifold. If there exists a Pfaffian form
is called a contact manifold. If there exists a Pfaffian form 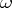 on
on  which defines the contact structure
which defines the contact structure 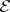 everywhere, i.e. if there exists a global everywhere non-zero section
everywhere, i.e. if there exists a global everywhere non-zero section 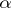 of
of 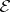 (so that
(so that 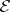 is a trivial bundle, or, as is also said, transversally orientable), then
is a trivial bundle, or, as is also said, transversally orientable), then 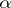 defines a strict contact structure and
defines a strict contact structure and 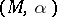 is a strict contact manifold with contact form
is a strict contact manifold with contact form 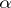 . In that case
. In that case 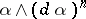 is a volume form on
is a volume form on 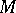 making
making 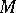 orientable. The unique vector field
orientable. The unique vector field 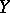 satisfying the contraction conditions
satisfying the contraction conditions  (i.e.
(i.e. 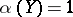 ) and
) and 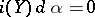 (i.e.
(i.e. 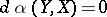 for all vector fields
for all vector fields 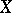 ) also satisfies
) also satisfies 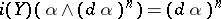 (and this is equivalent). It is sometimes called the Reeb vector field of
(and this is equivalent). It is sometimes called the Reeb vector field of 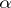 . By Darboux's theorem (cf. Pfaffian equation) a contact form
. By Darboux's theorem (cf. Pfaffian equation) a contact form 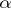 can be written locally in the form
can be written locally in the form
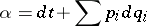 |
where 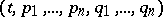 are local coordinates on
are local coordinates on 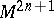 . The Reeb vector field in these coordinates is then given by
. The Reeb vector field in these coordinates is then given by 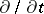 .
.
For more details on the above and the role of contact structures in mechanics, cf. [a2], Chapt. V. Contact structures on circle bundles over a symplectic manifold play an important role in the quantization theory of B. Kostant and J.-M. Souriau, cf. [a3]–[a5].
References
| [a1] | R. Abraham, "Foundations of mechanics" , Benjamin (1967) |
| [a2] | P. Libermann, C.-M. Marle, "Symplectic geometry and analytical mechanics" , Reidel (1987) (Translated from French) |
| [a3] | N.E. Hurt, "Geometric quantization in action" , Reidel (1983) |
| [a4] | B. Kostant, "Quantization and representation theory. Part 1: prequantization" , Lect. in Modern Anal. and Applications , 3 , Springer (1970) |
| [a5] | J.-M. Souriau, "Structures des systèmes dynamiques" , Dunod (1969) |
Contact structure. Ü. Lumiste (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contact_structure&oldid=19137