Contact scheme
contact network, contact circuit, switching circuit
A representation of a class of special control systems, one of the mathematical models of actual structures built from relay contacts. A contact network is a modelling class of control systems, and the same problems are considered for it as for other classes of control systems; it is particularly useful in the study of the "structural" properties of control systems.
A contact network 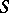 is obtained by attaching to each edge of some graph with selected vertices one of the letters of a finite alphabet
is obtained by attaching to each edge of some graph with selected vertices one of the letters of a finite alphabet 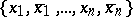 . The selected vertices are called the terminals or nodes of the network. An edge with a letter
. The selected vertices are called the terminals or nodes of the network. An edge with a letter 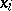 (or
(or 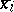 ) attached to it is called a make (respectively, break) contact. A sequence of contacts between two terminals
) attached to it is called a make (respectively, break) contact. A sequence of contacts between two terminals  and
and 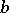 of
of 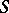 corresponding to a simple chain (or path) (see Graph) in the graph of
corresponding to a simple chain (or path) (see Graph) in the graph of 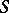 is called a chain between
is called a chain between  and
and 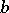 ; the conjunction of the corresponding letters is called the conductivity of the given chain. The conductivity between two terminals
; the conjunction of the corresponding letters is called the conductivity of the given chain. The conductivity between two terminals  and
and 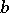 of the scheme is a Boolean function
of the scheme is a Boolean function 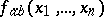 , equal to the disjunction of the conductivities of all chains between these terminals (when the set of chains between
, equal to the disjunction of the conductivities of all chains between these terminals (when the set of chains between  and
and 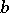 is empty,
is empty, 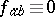 ; when
; when  coincides with
coincides with 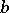 ,
, 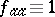 ). Associated with each contact network is a conductivity matrix
). Associated with each contact network is a conductivity matrix 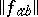 , the elements of which are the conductivities between pairs of terminals. Here,
, the elements of which are the conductivities between pairs of terminals. Here, 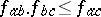 . Conversely, given a matrix of Boolean functions
. Conversely, given a matrix of Boolean functions 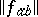 such that
such that 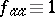 ,
, 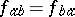 and
and 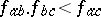 for any
for any 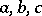 , there exists a contact network with given terminals for which the conductivities are the given
, there exists a contact network with given terminals for which the conductivities are the given 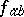 . In particular, there exists for any
. In particular, there exists for any 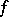 a two-terminal network the conductivity between the terminals of which is
a two-terminal network the conductivity between the terminals of which is 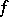 . In this case one says that the network realizes the function
. In this case one says that the network realizes the function 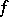 . For example, the network of Fig. arealizes the linear function
. For example, the network of Fig. arealizes the linear function 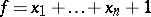 (
(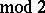 ).
).
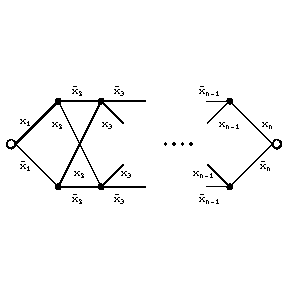
Figure: c025460a
Every Boolean function is realized by some contact network. Sometimes the set of all terminals in a contact network is divided into two subsets, the inputs and outputs. A contact network with  inputs and
inputs and  outputs is called a contact
outputs is called a contact 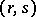 -terminal network. A contact network the conductivity between any pairs of outputs (or inputs) of which is zero, is called separating with respect to its outputs (or inputs). An example of a separating (with respect to outputs)
-terminal network. A contact network the conductivity between any pairs of outputs (or inputs) of which is zero, is called separating with respect to its outputs (or inputs). An example of a separating (with respect to outputs) 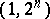 -terminal network is given by a contact tree (Fig. b).
-terminal network is given by a contact tree (Fig. b).
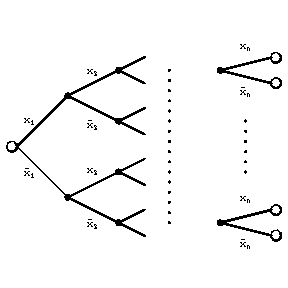
Figure: c025460b
A contact network is called planar if its graph with a source edge (that is, the edge joining the terminals to which no letter of the alphabet is attached) added is planar (see Graph, planar). A planar contact network 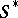 is said to be dual to a planar contact network
is said to be dual to a planar contact network 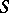 if the graph
if the graph 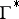 of
of 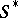 (with source edge) is dual to the corresponding graph
(with source edge) is dual to the corresponding graph 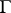 of
of 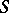 , where the source edge of
, where the source edge of 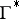 corresponds to that of
corresponds to that of 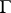 , while the remaining corresponding edges are ascribed the same letters (Fig. c).
, while the remaining corresponding edges are ascribed the same letters (Fig. c).
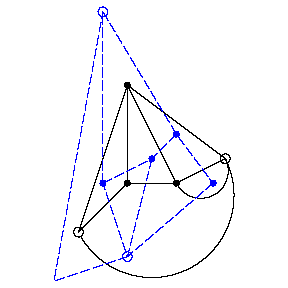
Figure: c025460c
The networks 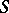 and
and 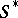 have the same number of contacts and realize dual functions (the duality principle). If the contacts of a network
have the same number of contacts and realize dual functions (the duality principle). If the contacts of a network 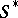 are replaced by their opposites, one obtains a network for the negation of the function realized by
are replaced by their opposites, one obtains a network for the negation of the function realized by 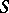 . In general, it is not possible to pass from non-planar contact networks to networks with the same number of contacts realizing dual functions. A
. In general, it is not possible to pass from non-planar contact networks to networks with the same number of contacts realizing dual functions. A 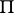 -network (parallel-series network) can be defined inductively: A contact network consisting of a single contact joining terminals is a
-network (parallel-series network) can be defined inductively: A contact network consisting of a single contact joining terminals is a 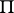 -network; a contact network constructed from two
-network; a contact network constructed from two 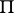 -networks joined in parallel or in series is a
-networks joined in parallel or in series is a 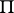 -network. There exists contact networks that are not
-network. There exists contact networks that are not 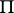 -networks, for example the network of Fig. d.
-networks, for example the network of Fig. d.
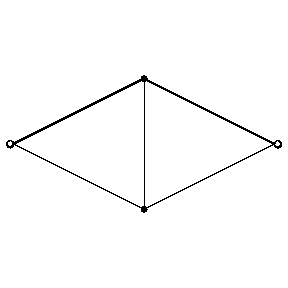
Figure: c025460d
The dual of a  -network is a
-network is a  -network. There is a correspondence between
-network. There is a correspondence between  -networks and formulas in
-networks and formulas in 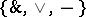 . Under this connection every
. Under this connection every  -network realizes the same function as the formula corresponding to it and contains as many contacts as there are letters in the formula. For example, corresponding to the network of Fig. e is the formula
-network realizes the same function as the formula corresponding to it and contains as many contacts as there are letters in the formula. For example, corresponding to the network of Fig. e is the formula
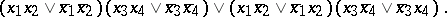 |
Figure: c025460e
The complexity of a contact network is the number of its contacts. The minimum number of contacts that suffice for the realization of an arbitrary Boolean function depending on  variables by a contact network is asymptotically equal to
variables by a contact network is asymptotically equal to 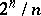 ; the minimum number of contacts sufficient for the realization by a
; the minimum number of contacts sufficient for the realization by a  -network is asymptotically equal to
-network is asymptotically equal to 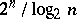 (see Synthesis problems).
(see Synthesis problems).
Two contact networks are said to be equivalent (under a given one-to-one correspondence between their terminals) if the conductivities between any pair of corresponding terminals of these networks are the same. On replacing some subnetwork 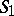 of a contact network
of a contact network 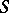 by an equivalent one, one obtains a network equivalent to
by an equivalent one, one obtains a network equivalent to 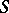 . (In this replacement it is necessary to consider as terminals of
. (In this replacement it is necessary to consider as terminals of 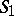 all terminals of
all terminals of 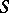 occurring in
occurring in 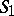 and all the vertices of
and all the vertices of 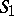 that are incident to contacts of
that are incident to contacts of 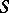 that are not in
that are not in 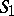 .) If
.) If 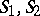 are equivalent networks, then the rule
are equivalent networks, then the rule 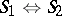 of equivalent transformation of contact networks enables one to replace, in any network, a subnetwork obtained from
of equivalent transformation of contact networks enables one to replace, in any network, a subnetwork obtained from 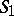 (or
(or 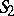 ) by a renaming of the letters, by the contact network obtained from
) by a renaming of the letters, by the contact network obtained from  (or
(or  ) by the same renaming.
) by the same renaming.
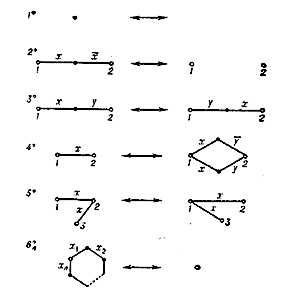
Figure: c025460f
There exists for each  a finite complete system of rules (Fig. f) enabling one to transfer between any two equivalent contact networks with number of variables not exceeding
a finite complete system of rules (Fig. f) enabling one to transfer between any two equivalent contact networks with number of variables not exceeding  . There does not, however, exist for the class of all contact networks (without restriction on the number of variables) a finite complete system of rules (if on applying the rules only renaming of letters is permitted).
. There does not, however, exist for the class of all contact networks (without restriction on the number of variables) a finite complete system of rules (if on applying the rules only renaming of letters is permitted).
References
| [1] | V.I. Shestakov, "Algebra of two-terminal networks built from two-terminal elements only (algebra of 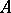 -networks)" Avtomatika i Telemekhanika , 6 : 2 (1941) pp. 15–24 (In Russian) -networks)" Avtomatika i Telemekhanika , 6 : 2 (1941) pp. 15–24 (In Russian) |
| [2] | C. Shannon, "A symbolic analysis of relay and switching circuits" AIEE Transact. , 57 (1938) pp. 713–723 |
| [3] | A. Nakasima, M. Hanzawa, "Theory of equivalent transformation of simple partial parts in relay circuits" Nippon Electr. Comm. Eng. : 9 (1938) pp. 32–39 |
| [4] | S.V. Yablonskii, "Functional constructions in 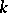 -valued logic" Trudy Math. Inst. Steklov. , 51 (1958) pp. 5–142 (In Russian) -valued logic" Trudy Math. Inst. Steklov. , 51 (1958) pp. 5–142 (In Russian) |
| [5] | A.V. Kuznetsov, "On a property of functions realizable by non-planar non-repetitive networks" Trudy Mat. Inst. Steklov. , 51 (1958) pp. 174–185 (In Russian) |
| [6] | I.A. Chegis, S.V. Yablonskii, "Logical methods for testing the operation of electrical circuits" Trudy Mat. Inst. Steklov. , 51 (1958) pp. 270–360 (In Russian) |
| [7a] | O.E. Lupanov, "On the synthesis of some class of control problems" Probl. Kibernet. , 10 (1963) pp. 63–97 (In Russian) |
| [7b] | O.B. Lupanov, "Complexity of formula realization of functions of logical algebra" Probl. Cybernetics , 3 (1962) pp. 782–811 Probl. Kibernet. , 3 (1960) pp. 61–80 |
| [7c] | O.B. Lupanov, "Ueber den Schaltaufwand bei den Realizierung logischer Funktionen" Probleme der Kibernetik , 3 (1963) pp. 68–90 Probl. Kibernet. , 3 (1960) pp. 61–80 |
| [8a] | V.L. Murskii, "On the equivalent transformations of switching circuits" Probl. Cybernetics , 5 (1964) pp. 77–98 Probl. Kibernet. , 5 (1961) pp. 61–76 |
| [8b] | W.L. Murski, "Ueber äquivalente Transformationen von Kontakt-Schaltungen" Probleme der Kibernetik , 5 (1964) pp. 44–64 Probl. Kibernet. , 5 (1961) pp. 61–76 |
Comments
References
| [a1] | S. Eilenberg, "Automata, languages and machines" , A , Acad. Press (1973) |
Contact scheme. N.A. Karpova (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contact_scheme&oldid=17371