Constant width, curve of
A plane convex curve for which the distance between any two pairs of parallel supporting lines is the same. This distance is called the width of the curve. Besides circles there are infinitely many other, generally speaking non-smooth, curves of constant width. The simplest of them is a Reuleaux triangle, consisting of three circular arcs of radius $a$ which connect the vertices of an equilateral triangle of side $a$ (see Fig. a).
The width of the Reuleaux triangle is equal to $a$. The area of the figure bounded by the Reuleaux triangle is $\frac{1}{2}a^2(\pi-\sqrt3)$. Among all curves of given width $a$ the Reuleaux triangle bounds a figure of least area. Other examples of curves of constant width, where the arcs of the curves of constant width circumscribed about different polygons are circular arcs, are shown in Fig. b. The length of a curve of a constant width $a$ is $\pi a$ (the Barbier theorem).
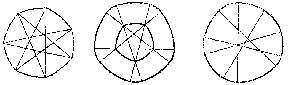
Figure: c025290b
The notion of a curve of constant width can be generalized to objects of higher codimension. Let $V$ be a smooth submanifold of an $n$-dimensional Euclidean space. The manifold $V$ is called a transnormal submanifold (see [2]) if for any point $p$ of $V$ the normal manifold $\nu(p)$ is such that for any point $q\in\nu(p)\cap V$ the condition $\nu(q)=\nu(p)$ holds. The class of plane transnormal curves coincides with the class of smooth curves of constant width (for more information on transnormal curves in space see ).
References
| [1] | W. Blaschke, "Kreis und Kugel" , Chelsea, reprint (1949) |
| [2] | S.A. Robertson, "Generalised constant width for manifolds" Michigan Math. J. , 11 (1964) pp. 97–105 |
| [3a] | B. Wegner, "Globale Sätze über Raumkurven konstanter Breite" Math. Nachr. , 53 (1972) pp. 337–344 |
| [3b] | B. Wegner, "Globale Sätze über Raumkurven konstanter Breite II" Math. Nachr. , 67 (1975) pp. 213–223 |
| [a1] | T. Bonnesen, W. Fenchel, "Theorie der konvexen Körper" , Springer (1934) |
| [a2] | S.A. Robertson, "Smooth curves of constant width and transnormality" Bull. London Math. Soc. , 16 (1984) pp. 264–274 |
Constant width, curve of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Constant_width,_curve_of&oldid=53386
