Configuration
A finite set of points, lines and planes related by mutual incidences (cf. Incidence) between them. Configurations can be both located in a place and in space.
A plane configuration is a finite system of $ p $ points and $ g $( straight) lines in the plane arranged in such a way that every point is incident to a fixed number $ \gamma $ of lines, while every line is incident to a fixed number $ \pi $ of points. A minimal system of points of a given configuration, from which the whole configuration can be obtained from incidence of pairs of points with lines and intersections of pairs of lines, is called a system of generators of the given configuration. The numbers $ p , g , \gamma , \pi $ are connected by the relation $ p \gamma = g \pi $, and the configuration is denoted by the symbol $ ( p _ \gamma , g _ \pi ) $. A configuration containing the same number of points and lines is denoted by the symbol $ ( p _ \gamma ) $.
Examples of plane configurations. 1) A single point and a single line incident to each other form the configuration $ ( 1 _ {1} ) $. 2) Three points not lying on a line and three lines incident with each pair forms the configuration $ ( 3 _ {2} ) $, this figure is a triangle or trigon in the plane. 3) The complete quadrilateral consisting of four lines and the six points of their pairwise intersections forms the configuration $ ( 6 _ {2} , 4 _ {3} ) $. However, here not all the lines joining pairs of points of the configuration are lines of the configuration; the points $ R , P , Q $ and the lines $ R P , R Q , P Q $ do not belong to it (Fig. a).
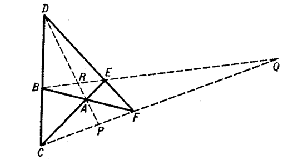
Figure: c024670a
An automorphism of a configuration is a mapping of this configuration onto itself under which points are taken to points, lines to lines and, furthermore, no incidence is lost and no new incidences are generated. A configuration is called regular if its automorphism group is transitive on the points and on the lines of the configuration.
For a given configuration $ ( p _ \gamma , g _ \pi ) $ the configuration $ ( g _ \pi , p _ \gamma ) $ is called its dual. The configurations of type $ ( p _ \gamma ) $, which are isomorphic to their dual, are called self-dual.
A configuration is called projective if the incidence of its elements is preserved under projective transformations. For example, the incidence of elements of some configurations in the projective plane satisfies the axioms for the latter and therefore the incidence of points and lines is preserved under projective transformations of this plane, so that the configuration is projective. All the incidences and elements of such a plane configuration can be drawn in a diagram by means of just a ruler. A plane configuration always has a dual, as a consequence of the duality principle.
A configuration can be defined as a finite partial plane. The possibility of the existence of a certain configuration is determined from geometrical and combinatorial relations between the collection of points and lines and the collection of incidences between them. A configuration can also be defined by means of an abstract scheme, for example, in the table (Fig. b) the incidences are shown (denoted by crosses) of four points and four planes, the vertices $ A _ {i} $ and the faces $ D _ {i} $
of a tetrahedron.
<tbody> </tbody>
|
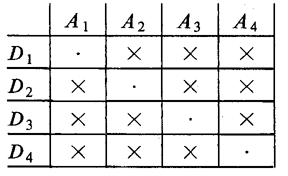
Figure: c024670b
Once a certain configuration has been abstractly defined, the question of its realization arises, that is, the possibility of constructing all incidences in terms of a given systems of generators. The realizability of a configuration as a finite partial plane entails the possibility of isomorphically mapping it onto a certain subplane of some plane.
A configuration $ ( p _ {2} ) $, $ p \geq 3 $, can be realized in the form of a $ p $- gon such that its vertices and sides are pairwise incident. The abstract scheme of a configuration $ ( 3 _ {2} ) $ can be constructed, for example, by a table as in Fig. b. Plane configurations $ ( p _ {3} ) $ are only possible for $ p \geq 7 $, since through every point of the configuration three lines must pass and each of them must contain two further points of the configuration (the number $ p $ must satisfy the inequality $ p ( p - 1 ) / 2 \geq 3 p $). In general there will be several non-isomorphic configurations of type $ ( p _ {3} ) $, the number of which depends on $ p $. The (abstractly speaking unique) configuration $ ( 7 _ {3} ) $ is represented by the scheme of Fig. c, where the number to the right of the bracket denotes the point of intersection of the lines passing through the pairs of points written to the left of the bracket, and the numbers beyond the vertical line denote those points that must be collinear for the validity of all the incidences indicated on the left.
$$ \left . \left . \begin{array}{c} 13 \\ {} \\ 24 \end{array} \right \} \begin{array}{c} {} \\ 5 \\ {} \end{array} \ \left . \begin{array}{c} 12 \\ {} \\ 34 \end{array} \right \} \begin{array}{c} {} \\ 6 \\ {} \end{array} \ \left . \begin{array}{c} 14 \\ {} \\ 23 \end{array} \right \} \begin{array}{c} {} \\ 7 \\ {} \end{array} \ \right | \begin{array}{c} {} \\ 567 \\ {} \end{array} $$
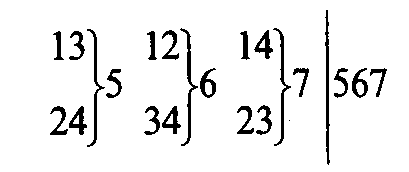
Figure: c024670c
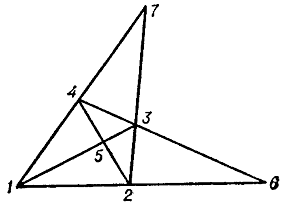
Figure: c024670d
In the real projective plane all the incidences are realized by the complete quadrangle (Fig. d), however, the last incidence (collinearity of three points) does not hold here. There are three non-isomorphic configurations $ ( 9 _ {3} ) $, one of which, $ ( 9 _ {3} ) _ {1} $, is called the Brianchon–Pascal configuration (Fig. e): Each line $ l _ {i} $ is incident with three distinct points $ a _ {i} $
and each point with three distinct lines.
<tbody> </tbody>
|
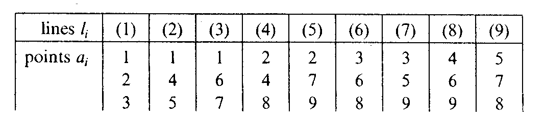
Figure: c024670e
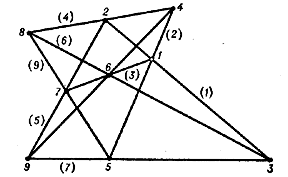
Figure: c024670f
The configuration can be realized in the projective plane (Fig. f); it is projective, regular and self-dual (see Brianchon theorem; Pascal theorem). The two other realizations of a configuration $ ( 9 _ {3} ) $, $ ( 9 _ {3} ) _ {2} $, $ ( 9 _ {3} ) _ {3} $, (Fig. g) are essentially different from the Brianchon–Pascal configuration.
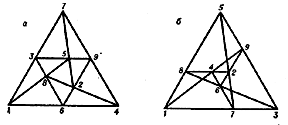
Figure: c024670g
For example, the configuration $ ( 9 _ {3} ) _ {3} $ is not regular, while the construction of $ ( 9 _ {3} ) _ {2} $ requires an auxiliary second-order curve. The configuration $ ( 10 _ {3} ) $ already has ten distinct non-isomorphic realizations, the most important of which is the Desarguesian configuration (Fig. h).
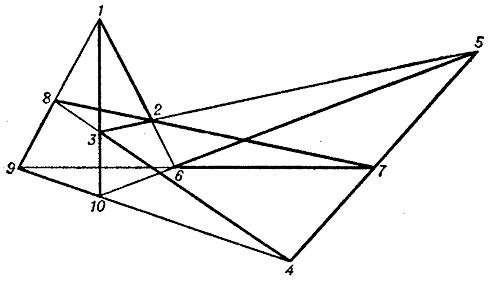
Figure: c024670h
It can be realized in the real projective plane, and is projective, regular, and self-dual. The other nine realizations of $ ( 10 _ {3} ) $ do not express any general geometrical theorem, and only eight of them can be realized in the real projective plane, but for their construction one requires a special arrangement of the system of generating points (in particular, a configuration of such a type can be realized in the form of regular polygons (Fig. i)).
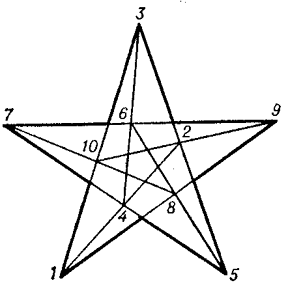
Figure: c024670i
In the one given in the diagram, the sequence of vertices is also obtained as a simultaneously inscribed and circumscribed decagon. The configurations $ ( 9 _ {3} ) $ and $ ( 10 _ {3} ) $ also admit of a geometric construction by means of mutually inscribed and circumscribed polygons; thus, the configuration $ ( 9 _ {3} ) _ {1} $ is represented in the form of an enneagon $ ( 2 , 3 , 6 , 1 , 5 , 9 , 4 , 8 , 7 , 2 ) $( Fig. f), the Desarguesian configuration in the form of a decagon $ ( 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 1 ) $( Fig. h). Such representations of these configurations are unique up to automorphisms. In general, the construction of mutually inscribed and circumscribed $ p $- gons leads to a configuration of type $ ( p _ {3} ) $. There also exists representations of configurations of type $ ( p _ {3} ) $ in the form of certain mutually inscribed and circumscribed polygons. For example, the Desarguesian configuration admits of a unique way (up to an automorphism) of representing a pair of mutually inscribed and circumscribed pentagons $ ( 1 , 9 , 7 , 5 , 3 ) $ and $ ( 8 , 4 , 10 , 6 , 2 ) $( Fig. h). As $ p $ increases, the number of non-isomorphic configurations of type $ ( p _ {3} ) $ rapidly increases.
A spatial configuration is a finite system of points and planes such that each point is incident to a fixed number of planes and each plane is incident to a fixed number of points. Along with configurations consisting of points and planes in space, one can also consider configurations consisting of points and lines. Thus, the Desarguesian configuration considered above, consisting of points and lines, is also a spatial configuration $ ( 10 _ {3} ) $( Fig. h) if the corresponding $ 3 $- gons lie in different planes. At the same time it can be regarded as the configuration $ ( 10 _ {3} , 5 _ {6} ) $ consisting of points and planes. The six vertices of corresponding triangles, the centre of perspectivity and the three points on the axis of perspectivity at which the corresponding sides of the trigons meet, given in total ten points. The three points formed by the respective sides of the $ 3 $- gons, and the two planes of the $ 3 $- gons themselves give in total five planes. In each plane there are six points of the configuration and each point is incident to three distinct planes.
A configuration $ ( 4 _ {3} ) $ is a trivial spatial configuration of type $ ( p _ \gamma ) $, its scheme is given in Fig. b; it is depicted by a tetrahedron. A configuration of type $ ( p _ {4} ) $ for $ p \leq 7 $ is not possible, for $ p = 8 $ there are three distinct schemes of the configuration, one of which is the so-called Möbius configuration consisting of two mutually inscribed and circumscribed tetrahedra. Each of the eight points, the vertices of the tetrahedra, is incident to four planes of the faces of the tetrahedra, and each of the four planes is incident of four vertices. For configurations of higher order, the number of distinct schemes rapidly increases; for example, a configuration $ ( 9 _ {4} ) $ already has 26 distinct geometric realizations.
The most remarkable of the spatial configurations of higher order are those of Reye and Schläfli. The so-called Reye configuration consists of the points and the planes of a configuration $ ( 12 _ {6} ) $. In real projective space this can be constructed, for example, from the vertices of a cube, its centre and the three points (at infinity) at which the parallel edges of the cube meet, while the planes of this configurations are the six faces of the cube and the six diagonal planes passing through pairs of opposite edges (Fig. j).
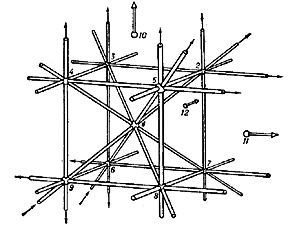
Figure: c024670j
The Reye configuration is projective, regular and self-dual, and a representation of this configuration can be constructed (according to the great duality principle) using an octahedron instead of a cube (Fig. k).
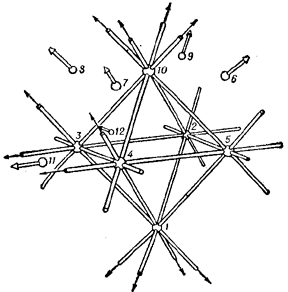
Figure: c024670k
The Reye configuration can also be regarded as the spatial configuration of points and lines $ ( 12 _ {4} , 16 _ {3} ) $.
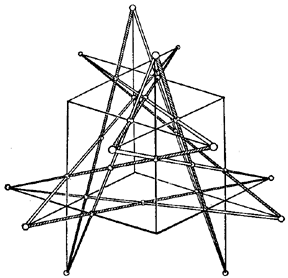
Figure: c024670l
The configuration $ ( 30 _ {2} , 12 _ {5} ) $, consisting of points and lines, is called the Schläfli double-six. It is depicted in space, for example, in the form of symmetrically-placed lines and points on each face of cube (with respect to one of the two sixes) (Fig. l).
Not every planar configuration can be realized in the real projective plane. For example, configurations $ ( 7 _ {3} ) $ and $ ( 8 _ {3} ) $ cannot be so realized, and in this connection the problem arises to realize the configuration in other projective planes. Each hypothesis asserting that the realizability in a given plane of some configuration with all the incidences except, perhaps, one, implies the realizability of the configuration with all its incidences, is called a configuration hypothesis of the given plane. Thus, if all the incidences of some configuration can be realized in some plane as a result of the geometric properties of this plane, then the configuration can be realized in this plane, i.e. is planar. For example, the configuration $ ( 9 _ {3} ) _ {1} $ can always be realized in the real projective plane, since, as a result of the theorems of Brianchon and Pascal, the realizability of all its incidences except one will imply that the last incidence will hold. In other words, these theorems are configuration hypotheses. The fulfillment of the last incidence in a configuration $ ( 7 _ {3} ) $( Fig. d) does not hold in such a plane (since the diagonal points of a complete quadrangle do not lie on a line). Therefore such an assertion is not a configuration hypothesis. However, it becomes one in the complex projective plane. In a similar way one may consider the realizability of other configurations; in particular, a configuration $ ( 8 _ {3} ) $ can be realized in the finite Pappus planes constructed over the Galois fields with three and four elements.
Configuration hypothesis that are valid in a given plane organize in a certain way the elements of this plane and therefore play a role in the axiomatic construction of the geometry of this plane. For example, if in a given plane all the axioms of a projective plane hold, but the Desarguesian configuration is not realized, then the given plane is a so-called non-Desarguesian geometry. A configuration hypothesis can also be described in algebraic form as a certain algebraic identity. In an arbitrary projective plane configuration hypotheses can only be introduced as new axioms, where the postulation of one configuration hypothesis may lead to the validity of other configuration hypotheses in this plane. Generally speaking, to every algebraic identity corresponds a configuration hypothesis, called the geometric representation of this identity in the plane in which the configuration is realized. (However, it is not established whether each configuration hypothesis is the geometric representation of a definite type of identity in the planar ternary ring or skew-field coordinatizing the projective plane.) The consideration of similar algebraic equivalents enables one to study both the properties of a configuration and the possibility of their realizability as a finite partial plane in a specific projective plane, and also the logical connection between different configuration hypotheses.
The theory of configurations finds application in the solution of a number of geometric problems. Thus, a plane configuration $ ( 8 _ {3} ) $ plays an important role in the theory of plane cubic curves without double points, in particular in the study of points of inflection. Reye configurations are applied in the study of regular polyhedra in a four-dimensional Euclidean space $ E ^ {4} $. A regular polyhedron in $ E ^ {4} $ is bounded by regions that are regular three-dimensional polyhedra. A regular polyhedron in $ E ^ {4} $ is called an $ n $- cell if it is bounded by $ n $ regular polyhedra. For example, a $ 5 $- cell is bounded by five three-dimensional tetrahedra, an $ 8 $- cell by eight cubes, etc., the $ 5 $- cell and the $ 24 $- cell being duals of each other (the points correspond to spaces and lines to planes). The study of regular cells is carried out by investigating their projections into $ E ^ {3} $. If for a $ 24 $- cell one chooses as the projection space some three-dimensional face, then the decomposition of the space into $ 12 $ octahedra is obtained; all of these, except the central one, extend to infinity, which leads to the kind of projection that is realized by the Reye configuration (Fig. j). If the projection space is chosen to be a three-dimensional space passing through a vertex of the $ 24 $- cell, then one also obtains the Reye configuration (Fig. k). (The projection of a $ 24 $- cell in three-dimensional space is depicted in Fig.13.)
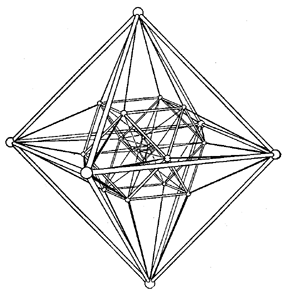
Figure: c024670m
The Reye configuration also arises in the system of points and axes of symmetry of four balls whose centres do not lie in a plane. In this system each axis is incident to three points and each point to four axes, and the spatial configuration $ ( 12 _ {4} , 16 _ {3} ) $ of points and lines is obtained. Each triple of points of symmetry defines the same plane, every two axes incident with a point of similarity form eight more distinct planes, in total twelve, each of which is incident with six points of similarity and each of the twelve points of similarity with six planes; that is, a configuration $ ( 12 _ {6} ) $ is obtained. The configuration represented by the Schläfli double-six is applied in the study of the properties of cubic algebraic surfaces. Such a cubic surface is defined by nineteen points and always passes through some Schläfli double-six. Here it is essential that any four lines of it have a hyperboloidal arrangement.
Configuration hypotheses on the realization of incidences in a plane are applied to the study of polyhedra (or polyangles) and to the solution of problems concerning the construction under various restrictions (structures with inaccessible elements, structures with a single ruler, etc.). The theory of configurations of polyhedra finds application in kinematics and graphical statics.
Configurations consisting of other geometric elements are possible, for example, consisting of discs of arbitrary dimension and unit radius in $ E ^ {n} $.
References
| [1] | D. Hilbert, S.E. Cohn-Vossen, "Anschauliche Geometrie" , Springer (1932) |
| [2] | L.A. Skornyakov, "Projective planes" Uspekhi Mat. Nauk , 6 : 6 (1951) pp. 112–154 (In Russian) |
| [3] | B.I. Argunov, "Configuration hypotheses and their algebraic equivalents" Mat. Sb. , 26 : 3 (1950) pp. 425–456 (In Russian) |
| [4] | F. Levi, "Geometrische Konfigurationen (mit einer Einführung in die kombinatorische Flächentopologie)" , S. Hirzel , Leipzig (1929) |
Comments
A planar configuration is a configuration that can be imbedded into a plane, perhaps in more than one way, whereas a plane configuration (also defined above) is a configuration in a plane.
If there exists a one-to-one correspondence between the sides of a polygon $ A $ and the vertices of a polygon $ B $ such that every side of $ A $ passes through the vertex of $ B $ corresponding to it, then $ A $ is said to be a circumscribed polygon with respect to $ B $ and $ B $ is said to be an inscribed polygon with respect to $ A $. Thus, in Fig. ga above the triangle 147 is circumscribed with respect to 369, which in turn is circumscribed with respect to 258, which in its turn is circumscribed with respect to 147.
A modern reference on configurations is [a3], Chapt. 3. For some material on the Schläfli six-fold in cubic surfaces cf. [a4], Chapt. 4.
This subject as described is no longer popular. On the one hand one has (finite) group theory, especially the theory of permutation groups (cf. Group; Finite group; Permutation group), where the geometrical nature of the objects being permuted usually is irrelevant. On the other hand, if one is interested in the configurations themselves and not in their group of automorphisms, then there are subjects like finite geometry (with objects of geometric nature) or the theory of block designs (cf. Block design) (where only the incidence relation is relevant).
A reference for these matters is [a2].
References
| [a1] | E. Steinitz, "Konfigurationen der projektiven Geometrie" W.F. Meyer (ed.) H. Mohrmann (ed.) , Enzyklopaedie der math. Wissenschaften , 3 , Teubner (1907–1910) pp. 481–516 |
| [a2] | R. Dembowski, "Finite geometries" , Springer (1968) pp. 254 |
| [a3] | F. Kärteszi, "Introduction to finite geometries" , North-Holland (1976) |
| [a4] | Yu.I. Manin, "Cubic forms. Algebra, geometry, arithmetic" , North-Holland (1984) (Translated from Russian) |
Configuration. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Configuration&oldid=53378