Complex moment problem, truncated
One of the interpolation problems in the complex domain.
Given a doubly indexed finite sequence of complex numbers $\gamma \equiv \gamma ^ { ( 2 n ) }$:
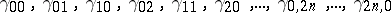 |
with $\gamma_{00}> 0$ and $\gamma _ { i j } = \overline { \gamma } _ { ji }$, the truncated complex moment problem entails finding a positive Borel measure $\mu$ supported in the complex plane $\mathbf{C}$ such that
\begin{equation*} \gamma _ { i j } = \int \overline{z} ^ { i } z ^ { j } d \mu , 0 \leq i + j \leq 2 n; \end{equation*}
$\gamma$ is a truncated moment sequence (of order $2 n$) and $\mu$ is a representing measure for $\gamma$. The truncated complex moment problem serves as a prototype for several other moment problems to which it is closely related: the full complex moment problem prescribes moments of all orders, i.e., $\gamma = ( \gamma _ { i j } ) _ { i , j \geq 0 }$; the $K$-moment problem (truncated or full) prescribes a closed set $K \subseteq \mathbf{C}$ which is to contain the support of the representing measure [a26]; and the multi-dimensional moment problem extends each of these problems to measures supported in $\mathbf{C} ^ { k }$ [a14]; moreover, the $k$-dimensional complex moment problem is equivalent to the $2 k$-dimensional real moment problem [a8]. All of these problems generalize classical power moment problems on the real line, whose study was initiated by Th.J. Stieltjes (1894), H. Hamburger (1920–1921), F. Hausdorff (1923), and M. Riesz (1923) (cf. also Moment problem and [a1], [a27]).
The truncated complex moment problem is also related to subnormal operator theory [a24], [a29], [a31], polynomial hyponormality [a11], and joint hyponormality [a32], [a33] (cf. also Semi-normal operator). Indeed, A. Atzmon [a2] used subnormal operator theory to solve the full complex moment problem for the disc, and M. Putinar [a18] found a related but different solution to the disc problem based on hyponormal operator theory. More generally, K. Schmüdgen [a26] used an approach based on operator theory and semi-algebraic geometry to obtain the following existence theorem for representing measures [a26] in the multi-dimensional full $K$-moment problem for the case when $K$ is compact and semi-algebraic; this result encompasses several previously known special cases (cf. [a4], [a5], [a15], [a17]).
Let $E$ denote the multi-shift operator on multi-sequences and let $R = \{ r _ { 1 } , \dots , r _ { m } \}$ be a finite subset of $\mathbf{R}[ x _ { 1 } , \dots , x _ { n } ]$. Suppose that the semi-algebraic set $K _ { R } \equiv \{ x \in \mathbf{R} ^ { n } : r_j ( x ) \geq 0 , j = 1 , \ldots , m \}$ is compact. Then an $n$-dimensional full (real) moment sequence $\gamma$ has a representing measure supported in $K _ { R }$ if and only if the quadratic forms associated with $\gamma$ and $p ( E ) ( \gamma )$ are positive semi-definite (for every $p$ that is a product of distinct $r _ { j }$).
For general closed sets $K \subseteq \mathbf{R} ^ { n }$, the full $K$-moment problem continues (1998) to defy a complete solution. Hamburger's classical theorem (1920) gives necessary and sufficient conditions for the solvability of the full moment problem on the real line, i.e., $K = \mathbf{R}$: A real sequence $\beta \equiv ( \beta _ { j } ) _ { j \geq 0 }$ with $\beta _ { 0 } > 0$ has a representing measure supported in $\mathbf{R}$ if and only if for each 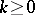 , the Hankel matrix $H ( k ) \equiv ( \beta _ { i + j } ) _ { 0 \leq i , j \leq k }$ is positive semi-definite (cf. also Nehari extension problem; Synthesis problems). Hamburger's theorem serves as a prototype for much of moment theory, because it provides a concrete criterion closely related to the moments. Nevertheless, when $K = \mathbf{R} ^ { n }$ ($n > 1$), positivity alone is not sufficient to imply the existence of a representing measure [a3], [a14], [a25] and a concrete condition for solvability of the $K = \mathbf{R} ^ { n }$ full moment problem (including solvability of the full complex moment problem for $K = \mathbf{C}$) remains unknown (to date, 1999, perhaps the most definitive and comprehensive treatments of the full multi-dimensional $K$-moment problem can be found in [a38], [a39]).
, the Hankel matrix $H ( k ) \equiv ( \beta _ { i + j } ) _ { 0 \leq i , j \leq k }$ is positive semi-definite (cf. also Nehari extension problem; Synthesis problems). Hamburger's theorem serves as a prototype for much of moment theory, because it provides a concrete criterion closely related to the moments. Nevertheless, when $K = \mathbf{R} ^ { n }$ ($n > 1$), positivity alone is not sufficient to imply the existence of a representing measure [a3], [a14], [a25] and a concrete condition for solvability of the $K = \mathbf{R} ^ { n }$ full moment problem (including solvability of the full complex moment problem for $K = \mathbf{C}$) remains unknown (to date, 1999, perhaps the most definitive and comprehensive treatments of the full multi-dimensional $K$-moment problem can be found in [a38], [a39]).
In a different direction, M. Riesz (1923) proved that $\beta$ (as above) has a representing measure supported in a closed set $K \subset \bf R$ if and only if whenever a polynomial $a _ { 0 } + a _ { 1 } t + \ldots + a _ { n } t ^ { n }$ (with complex coefficients) is non-negative on $K$, then $a _ { 0 } \beta _ { 0 } + a _ { 1 } \beta _ { 1 } + \ldots + a _ { n } \beta _ { n } \geq 0$. E.K. Haviland (1935, [a16]) subsequently extended this result to the multi-variable full $K$-moment problem. Although Riesz' theorem solves the full moment problem in principle, it is very difficult to verify the Riesz criterion for a particular sequence $\beta$ unless $K$ is a half-line (the case studied by Stieltjes), an interval (the case studied by Hausdorff) or, as in Schmüdgen's theorem, when $K$ is compact and semi-algebraic. The intractability of the Riesz–Haviland criterion is related to lack of an adequate structure theory for multi-variable polynomials that are non-negative on a given set $K$ [a5], [a14], [a20], [a22]; in particular, D. Hilbert (1888) established the existence of a polynomial, non-negative on the real plane, that cannot be represented as a sum of squares of polynomials (cf. [a3], [a14], [a25]).
Because a truncated moment problem is finite in nature, one expects that in cases where a truncated moment problem is solvable, it should be possible to explicitly construct finitely atomic representing measures by elementary methods. (See below for such a construction for the truncated complex moment problem.) From this point of view, the multi-variable truncated $K$-moment problem subsumes the multi-variable quadrature problem of numerical analysis (cf. [a6], [a13], [a23], [a31]). In addition, J. Stochel [a28] has proven that if $\gamma$ is a multi-variable full moment sequence, and if for each $n$ the truncated sequence $\gamma ^ { ( 2 n ) }$ has a representing measure $\mu _ { n }$ supported in a closed set $K$, then some subsequence of $\{ \mu _ { n } \}$ converges (in an appropriate weak topology) to a representing measure $\mu$ for $\gamma$ with $\operatorname{supp} \mu \subseteq K$. Thus, a complete solution of the truncated $K$-moment problem would imply a solution to the full $K$-moment problem.
Truncated multi-variable moment problems can be analyzed via the positivity and extension properties of the associated moment matrices [a7], [a8]. For the truncated complex moment problem, one associates to $\gamma \equiv \gamma ^ { ( 2 n ) }$ the moment matrix $M ( n ) \equiv M ( n ) ( \gamma )$, with rows and columns indexed by $1, Z , \bar{Z} , Z ^ { 2 } , \bar{Z} Z , Z ^ { 2 } , \ldots , Z ^ { n } , \ldots , \bar{Z} ^ { n }$, as follows: the entry in row $z ^ { k } Z ^ { l }$ and column $Z ^ { i } Z ^ { j }$ is $\gamma _ { i + l ,\, j + k}$. Thus, if $\mu$ is a representing measure for $\gamma$ and $p , q \in P _ { n }$ (the set of polynomials in $z, \overline{z}$ of degree at most $n$), then $\int p \overline { q } d \mu = \langle M ( n ) \hat { p } , \hat { q } \rangle$. Here, $\hat { p }$ denotes the coefficient vector of $p$ with respect to the above lexicographic ordering of the monomials in $P_n$. In particular, it follows that $M ( n )$ is positive semi-definite and that the support of $\mu$ contains at least $r \equiv \operatorname { rank } M ( n )$ points [a8] (cf. [a30]).
It can be proven [a8] that $\gamma ^ { ( 2 n ) }$ has a rank-$M ( n )$-atomic (minimal) representing measure if and only if $M ( n ) \geq 0$ and $M ( n )$ admits an extension to a moment matrix $M ( n + 1 )$ satisfying $ \operatorname { rank } M ( n + 1 ) = \operatorname { rank } M ( n )$.
If $M ( n )$ admits such a flat extension $M ( n + 1 )$ (i.e. an extension that preserves rank), then there is a relation $Z ^ { n + 1 } = p ( Z , \overline{Z} ) \equiv \sum _ { 0 \leq i + j \leq n } a _ { i j } \overline{Z} ^ { i } Z ^ { j }$ in $\operatorname { Col } M ( n + 1 )$ (the column space of $M ( n + 1 )$). It can be shown [a8], Chap. 5, that $M ( n + 1 )$ then admits unique successive flat (positive) extensions $M ( n + 2 ) , M ( n + 3 ) , \ldots$, where $M ( n + k + 1 )$ is determined by $Z ^ { n + k + 1 } = \sum a_{i j } \bar{Z} ^ { i } Z ^ { j + k }$ in $\operatorname { Col} M ( n + k + 1 )$ ($k \geq 1$). The resulting infinite moment matrix $M \equiv M ( \infty )$ induces a semi-inner product on $\mathbf{C} [ z , \overline{z} ]$ by $( p , q ) _ { M } = \langle M \hat { p } , \hat { q } \rangle$. The space
\begin{equation*} N = \{ p : ( p , p ) _ { M } = 0 \} \end{equation*}
is an ideal in $\mathbf{C} [ z , \overline{z} ]$, and $\mathbf{C} [ z , \overline{z} ] / N$ is an $r$-dimensional Hilbert space on which the multiplication operator $M _ { z }$ is normal [a8], Chap. 4. The spectrum of $M _ { z }$ (cf. also Spectrum of a matrix) then provides the support for the unique ($r$-atomic) representing measure $\mu$ associated with the flat extension $M ( n + 1 )$.
To explicitly construct $\mu$, note that since $\operatorname { rank } M = \operatorname { rank } M ( n ) = r$, there is a linear relation $Z ^ { r } = a _ { 0 } 1 + \ldots + a _ { r - 1 } Z ^ { r - 1 }$ in $\operatorname{Col} M$ (or, equivalently, in $\operatorname{Col} M ( r )$, since $M \geq 0$ [a12]). The polynomial $g ( z ) = z ^ { r } - ( a _ { 0 } + \ldots + a _ { r - 1 } ^ { r - 1 } )$ has $r$ distinct complex roots, $z_{0} , \dots , z _ { r - 1}$, which provide the support of $\mu$, and the densities $\rho_i$ for $\mu \equiv \sum \rho _ { i } \delta _ { z _ { i } }$, are uniquely determined by the Vandermonde equation
\begin{equation*} V ( z _ { 0 } , \dots , z _ { r - 1} ) ( \rho _ { 0 } , \dots , \rho _ { r - 1 } ) ^ { T } = ( \gamma _ { 00 } , \dots , \gamma _ { 0 , r - 1 } ) ^ { T } \end{equation*}
[a8], Chap. 4.
Results of [a10] and [a23] imply that the most general finitely atomic representing measures for $\gamma$ correspond to positive, finite-rank moment matrix extensions $M ( \infty )$ of $M ( n )$. Such an extension $M ( \infty )$ exists if and only if $M ( n )$ admits a positive extension $M ( n + k )$, which in turn admits a flat extension $M ( n + k + 1 )$ [a10]. Examples for which $k > 0$ is required are provided in [a37]. On the other hand, examples in [a3], [a25] imply that a positive, infinite rank $M ( \infty )$ need not correspond to any representing measure for $\gamma$.
The preceding results suggest the following flat extension problem [a9], [a10]: under what conditions on $\gamma$ does $M ( n ) ( \geq 0 )$ admit a flat extension $M ( n + 1 )$? Among the necessary conditions for a flat extension is the condition that $M ( n )$ be recursively generated, i.e. $p , q \in P ( n )$, $p ( Z , \overline{Z} ) = 0$ imply $( p q ) ( Z , \overline{Z} ) = 0$. Although not every recursively generated positive moment matrix admits a flat extension (or even a representing measure [a10], [a36]), several positive results are known:
i) [a8] If $M ( 1 ) \geq 0$, then $\gamma$ admits a rank-$M ( 1 )$ atomic representing measure.
ii) [a9] If $M ( n ) \geq 0$ is recursively generated and if there exist $\alpha , \beta \in \bf{C}$ such that $\overline{Z} = \alpha 1 + \beta Z$ in $\operatorname{Col} M ( n )$, then $M ( n )$ admits infinitely many flat extensions, each corresponding to a distinct rank $M ( n )$-atomic (minimal) representing measure for $\gamma$.
iii) [a9] If $M ( n ) \geq 0$ is recursively generated and if $Z ^ { k } = p ( Z , \overline{Z} )$ in $\operatorname{Col} M ( n )$ for some $p \in P _ { k - 1 }$, where $k \leq [ n / 2 ] + 1$, then $M ( n )$ admits a unique flat extension $M ( n + 1 )$.
The preceding approach can be extended to truncated moment problems in any number of real or complex variables; to do this one defines moment matrices subordinate to lexicographic orderings of the variables [a8]. In the case of one real variable, such moment matrices are the familiar Hankel matrices, and the theory subsumes the truncated moment problems of Stieltjes, Hamburger, and Hausdorff [a7] (cf. also Moment problem).
A refinement of the moment matrix technique also leads to an analogue of Schmüdgen's theorem for minimal representing measures in the truncated $K$-moment problem for semi-algebraic sets. Given $M ( n )$, $k \leq m$, and a polynomial $p ( z , \bar{z} )$ of degree $2 k$ or $2 k - 1$, there exists a unique matrix $M _ { p } ( n )$ such that $\langle M _ { p } ( n )\, \hat { f } , \hat {g} \rangle = \tau (\, p\, f \overline{g} )$ ($f , g \in P _ { n-k } $), where $\tau ( \sum a _ { i j }\overline{z} ^ { i } z ^ { j } ) = \sum a _ { i j } \gamma _ { i j }$; $M _ { p } ( n )$ may be expressed as a linear combination of compressions of $M ( n )$.
Let $1 , \dots , r _ { m } \in \mathbf{C} [ z , \overline{z} ]$, with $\operatorname { deg } r _ { j } = 2 k _ { j }$ or $2 k_{ j} - 1$. There exists [a34] a rank-$M ( n )$-atomic (minimal) representing measure for $\gamma ^ { ( 2 n ) }$ supported in
\begin{equation*} K _ { R } \equiv \{ z : r _ { j } ( z , \overline{z} ) \geq 0 ,\; j = 1 , \ldots , m \} \end{equation*}
if and only if $M ( n )$ admits a flat extension $M ( n + 1 )$ for which $M _ { r_{j} } ( n + k _ { j } ) \geq 0$ (relative to the uniquely determined flat extension $M ( n + k _ { j } )$), $j = 1 , \ldots , m$.
For additional recent (1999) results on the truncated $K$-moment problem, see [a35], [a36].
References
| [a1] | N.J. Akhiezer, "The classical moment problem" , Hafner (1965) MR0184042 Zbl 0135.33803 |
| [a2] | A. Atzmon, "A moment problem for positive measures on the unit disc" Pacific J. Math. , 59 (l975) pp. 317–325 MR0402057 Zbl 0319.44009 |
| [a3] | C. Berg, T.P.R. Christensen, C.U. Jensen, "A remark on the multidimensional moment Problem" Math. Ann. , 223 (1979) pp. 163–169 MR0543726 Zbl 0416.46003 |
| [a4] | C. Berg, P.H. Maserick, "Polynomially positive definite sequences" Math. Ann. , 259 (1982) pp. 187–495 MR0660043 Zbl 0486.44004 |
| [a5] | G. Cassier, "Probléme des moments sur un compact de ${\bf R} ^ { n }$ et décomposition des polynômes a plusiers variables" J. Funct. Anal. , 58 (1984) pp. 254–266 |
| [a6] | R. Cools, P. Rabinowitz, "Monomial cubature rules since `Stroud': a compilation" J. Comput. Appl. Math. , 48 (1993) pp. 309–326 |
| [a7] | R. Curto, L. Fialkow, "Recursiveness, positivity, and truncated moment problems" Houston J. Math. , 17 (1991) pp. 603–635 MR1147276 Zbl 0757.44006 |
| [a8] | R. Curto, L. Fialkow, "Solution of the truncated complex moment problem for flat data" Memoirs Amer. Math. Soc. , 119 (1996) MR1303090 Zbl 0876.30033 |
| [a9] | R. Curto, L. Fialkow, "Flat extensions of positive moment matrices: relations in analytic or conjugate terms" H. Bercovici (ed.) et al. (ed.) , Nonselfadjoint Operator Algebras, Operator Theory, and Related Topics , Birkhäuser (1998) pp. 59–82 MR1639649 Zbl 0904.30020 |
| [a10] | R. Curto, L. Fialkow, "Flat extensions of positive moment matrices: recursively gnereated relations" Memoirs Amer. Math. Soc. , 136 (1998) |
| [a11] | R. Curto, M. Putinar, "Nearly subnormal operators and moment problems" J. Funct. Anal. , 115 (1993) pp. 480–497 MR1234402 Zbl 0817.47026 |
| [a12] | L. Fialkow, "Positivity, extensions and the truncated complex moment problem" Contemp. Math. , 185 (1995) pp. 133–150 MR1332058 Zbl 0830.44007 |
| [a13] | L. Fialkow, "Multivariable quadrature and extensions of moment matrices" Preprint (1996) |
| [a14] | B. Fuglede, "The multidimensional moment problem" Exposition Math. , 1 (1983) pp. 47–65 MR0693807 Zbl 0514.44006 |
| [a15] | F. Hausdorff, "Momentprobleme fur ein endliches Intervall" Math. Z. , 16 (1923) pp. 220–248 MR1544592 Zbl 49.0193.01 |
| [a16] | E.K. Haviland, "On the momentum problem for distributions in more than one dimension, I–II" Amer. J. Math. , 57/58 (1935/1936) pp. 562–568; 164–168 |
| [a17] | J.L. McGregor, "Solvability criteria for certain $N$-dimensional moment problems" J. Approx. Th. , 30 (1980) pp. 315–333 |
| [a18] | M. Putinar, "A two-dimensional moment problem" J. Funct. Anal. , 80 (1988) pp. 1–8 MR0960218 Zbl 0668.47024 |
| [a19] | M. Putinar, "The L problem of moments in two dimensions" J. Funct. Anal. , 94 (1990) pp. 288–307 MR1081646 Zbl 0735.47008 |
| [a20] | M. Putinar, "Positive polynomials on compact semi-algebraic sets" Indiana Univ. Math. J. , 42 (1993) pp. 969–984 MR1254128 Zbl 0796.12002 |
| [a21] | M. Putinar, "Extremal solutions of the two-dimensional L-problem of moments" J. Funct. Anal. , 136 (1996) pp. 331–364 MR1380658 Zbl 0917.47014 |
| [a22] | M. Putinar, "Linear analysis of quadrature domains" Ark. Mat. , 33 (1995) pp. 357–376 MR1373029 Zbl 0892.47025 |
| [a23] | M. Putinar, "On Tchakaloff's theorem" preprint (1995) |
| [a24] | D. Sarason, "Moment problems and operators on Hilbert space" Moments in Math. — Proc. Sympos. Appl. Math. , 37 (1987) pp. 54–70 MR921084 |
| [a25] | K. Schmüdgen, "An example of a positive polynomial which is not a sum of squares. A positive but not strongly positive functional" Math. Nachr. , 88 (1979) pp. 385–390 MR543417 |
| [a26] | K. Schmüdgen, "The K-moment problem for semi-a1gebraic sets" Math. Ann. , 289 (1991) pp. 203–206 |
| [a27] | J. Shohat, J. Tamarkin, "The problem of moments" , Math. Surveys , I , Amer. Math. Soc. (1943) MR0008438 Zbl 0063.06973 |
| [a28] | J. Stochel, "private communication" private communication (1994) |
| [a29] | J. Stochel, F. Szafraniec, "A characterisation of subnormal operators, spectral theory of linear operators and related topics" , Birkhäuser (1984) pp. 261–263 |
| [a30] | J. Stochel, F. Szafraniec, "Algebraic operators and moments on algebraic sets" Portug. Math. , 51 (1994) pp. 1–21 MR1281954 Zbl 0815.47058 |
| [a31] | V. Tchakaloff, "Formules de cubatures mécaniques à coefficients non négatifs" Bull. Sci. Math. , 81 (1957) pp. 123–134 MR0094632 Zbl 0079.13908 |
| [a32] | R. Curto, L. Fialkow, "Recursively generated weighted shifts and the subnormal completion problem" Integral Eq. Operator Th. , 17 (1993) pp. 202–216 MR1233668 Zbl 0804.47028 |
| [a33] | R. Curto, L. Fialkow, "Recursively generated weighted shifts and the subnormal completion problem II" Integral Eq. Operator Th. , 18 (1994) pp. 369–426 MR1265443 Zbl 0807.47016 |
| [a34] | R. Curto, L. Fialkow, "The truncated complex $K$-moment problem" Trans. Amer. Math. Soc. (to appear) MR1303090 Zbl 0876.30033 |
| [a35] | R. Curto, L. Fialkow, "The quadratic moment problem for the unit circle and unit disk" Preprint (1999) MR1799648 Zbl 0979.44006 |
| [a36] | R. Curto, L. Fialkow, "The quartic complex moment problem" Preprint (1999) |
| [a37] | L. Fialkow, "Minimal representing measures arising from constant rank-increasing moment matrix extensions" J. Operator Th. (to appear) |
| [a38] | M. Putinar, F. Vasilescu, "Solving moment problems by dimensional extension" Preprint (1998) MR1709313 MR1679992 Zbl 0939.44003 Zbl 0931.44004 |
| [a39] | J. Stochel, F. Szafraniec, "The complex moment problem and subnormality: A polar decomposition approach" J. Funct. Anal. , 159 (1998) pp. 432–491 MR1658092 MR1709313 Zbl 1048.47500 |
Complex moment problem, truncated. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complex_moment_problem,_truncated&oldid=50767