Chebyshev pseudo-spectral method
A type of trigonometric pseudo-spectral method (cf. Trigonometric pseudo-spectral methods). See also Fourier pseudo-spectral method.
A Chebyshev polynomial is defined as $T _ { n } ( x ) = \operatorname { cos } ( n \operatorname { cos } ^ { - 1 } x )$ (cf. also Chebyshev polynomials). If $x = \operatorname { cos } \theta$, the resulting Chebyshev function is truly an $n$th order polynomial in $x$, but it is also a cosine function with a change of variable. Thus, a finite Chebyshev series expansion is related to a discrete cosine transform.
The Chebyshev pseudo-spectral method is the most logical choice of pseudo-spectral methods for problems with non-periodic boundary conditions. This comes from the particularly nice characteristics of the Chebyshev interpolating polynomials (cf. also Chebyshev polynomials).
Of all $( N + 1 )$st degree polynomials, with leading coefficient $1$, $T _ { N + 1 } / 2 ^ { N }$ has the smallest maximum on the interval $[ - 1,1 ]$. Thus, in Lagrangian interpolation (see also Lagrange interpolation formula), if the interpolation points are taken to be the zeros of this polynomial, the error is minimized. A related and possibly more useful set of interpolation points are the extrema of $T _ { N } ( x )$: $x _ { j } = \operatorname { cos } ( \pi j / N )$, $j = 0 , \dots , N$, called the Gauss–Lobatto points.
The trigonometric interpolation 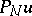 of the function $u$ at the Gauss–Lobatto points is $P _ { N } u = \sum _ { j = 0 } ^ { N } u ( x _ { j } ) C _ { j } ( x )$, where $C_{j}$ is the Cardinal function
of the function $u$ at the Gauss–Lobatto points is $P _ { N } u = \sum _ { j = 0 } ^ { N } u ( x _ { j } ) C _ { j } ( x )$, where $C_{j}$ is the Cardinal function
\begin{equation*} C _ { j } = ( 1 - x ^ { 2 } ) \frac { T _ { N } ^ { \prime } ( x ) ( - 1 ) ^ { j + 1 } } { [ \bar{c} _ { j } N ^ { 2 } ( x - x _ { j } ) ] }, \end{equation*}
with $\overline { c }_ 0 = \overline { c } _ { N } = 2$, $\overline{ c }_{j} = 1$ otherwise. Rearranging, the interpolation polynomial becomes a finite Chebyshev series $P _ { N } u ( x ) = \sum _ { n = 0 } ^ { N } a _ { n } T _ { n } ( x )$, where the Chebyshev coefficients are
\begin{equation*} a _ { n } = \frac { 2 } { N } \frac { 1 } { \overline { c } _ { n } } \sum _ { j = 0 } ^ { N } u ( x _ { j } ) \frac { T _ { n } ( x _ { j } ) } { \overline { c } _ { j } }. \end{equation*}
Suppose the equation $L u = f$ is to be solved, where $L$ is a differential operator, $f$ is a given function and $u$ is an unknown function. In the Chebyshev pseudo-spectral method, the solution $u$ is approximated by a Chebyshev interpolating polynomial. In the Lagrangian polynomial or "grid-point representation" , the problem can be written as $L _ { i , j } u _ { j } = f _ { i }$, where $L _ { i ,\, j } = L C _ { j } ( x ) |_ { x = x _ { i } }$. The form of $L_{i ,\, j}$ can be found through differentiation of the Cardinal function: $C _ { j } ( x _ { i } ) = \delta _ { i , j }$,
\begin{equation*} \frac { d C _ { j } } { d x } ( x _ { k } ) = \left\{ \begin{array} { l l } { \frac { 1 } { 6 } ( 1 + 2 N ^ { 2 } ) } & { \text { for } j = k = 0 ,} \\ { - \frac { 1 } { 6 } ( 1 + 2 N ^ { 2 } ) } & { \text { for } j = k = N, } \\ { - \frac { x _ { j } } { 2 ( 1 - x _ { j } ^ { 2 } ) } } & { \text { for } j = k , 0 < j < N ,} \\ { ( - 1 ) ^ { j + k } \frac { \bar{c} _ { k } } { \bar{c} _ { j } ( x _ { k } - x _ { j } ) } } & { \text { for } j \neq k, } \end{array} \right. \end{equation*}
and $( d ^ { k } C _ { j } / d x ^ { k } ) ( x _ { i } ) = [ ( d C _ { j } / d x ) ( x _ { i } ) ] ^ { k }$. Note that derivatives require $O ( N ^ { 2 } )$ operations.
Another way to find an expression for the derivative is to differentiate the Chebyshev series, which means differentiating the Chebyshev polynomials and using the recurrence relation for derivatives of Chebyshev polynomials, $d ( P _ { N } u ) / d x = \sum _ { n = 0 } ^ { N } b _ { n } T _ { N } ( x )$, where $b _ { N } = 0$, $b _ { N - 1 } = 2 N a _ { N }$, $\overline{c} _ { n } b _ { n } = b _ { n + 2 } + 2 ( n + 1 ) a _ { n + 1 }$ for $0 \leq n < N - 1$. Thus, in coefficient representation, the derivative can be evaluated in $O ( N )$ operations while non-linear terms or multiplication by non-constant coefficients require $O ( N ^ { 2 } )$. The fast discrete cosine transform can be used to switch between spectral and grid point representations.
References
| [a1] | J.P. Boyd, "Chebyshev and Fourier spectral methods" , Dover (2000) (pdf version: http://www-personal.umich.edu/~jpboyd/BOOK_Spectral2000.html) |
| [a2] | D. Gottlieb, S.A. Orszag, "Numerical analysis of spectral methods: Theory and applications" , SIAM (1977) |
| [a3] | C. Canuto, M.Y. Hussaini, A. Quarteroni, T.A. Zang, "Spectral methods in fluid dynamics" , Springer (1987) |
| [a4] | D. Gottlieb, M.Y. Hussaini, S.A. Orszag, "Theory and application of spectral methods" R.G. Voigt (ed.) D. Gottlieb (ed.) M.Y. Hussaini (ed.) , Spectral Methods for Partial Differential Equations , SIAM (1984) |
| [a5] | B. Fornberg, "A practical guide to pseudospectral methods" , Cambridge Monographs Appl. Comput. Math. , 1 , Cambridge Univ. Press (1996) |
Chebyshev pseudo-spectral method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebyshev_pseudo-spectral_method&oldid=55316