Cartographic projection
map projection
The representation, on the plane, of all or part of the terrestrial ellipsoid. Usually this representation is determined having in mind the drawing of a map.
Cartographic projections are drawn in a specified scale. By reducing the ideal terrestrial ellipsoid $ M $ times, one obtains a geometric model of it, a globe, the mapping of which, in natural size, onto the plane gives a map of the surface of this ellipsoid. The ratio $ 1:M $ represents the representative fraction called the principal scale of the map. The fundamental characteristic of a map projection at any point of it is, however, the actual scale $ \mu $. This is the inverse of the fraction obtained by dividing an infinitely small segment $ dS $ on the terrestrial ellipsoid by its image $ d \sigma $ on the plane: $ 1/ \mu = dS/d \sigma $. The number $ \mu $ depends on the position of the point on the ellipsoid and on the direction of the chosen segment. The ratio $ \mu /M $ is called the relative scale or linear distortion, the difference $ ( \mu /M) - 1 $ is called the linear deformation. The numerical value of the principal scale $ M $ is taken into account only in the calculation of the coordinates of points of a map projection and in the use of maps; in the study of map projections one sets $ M = 1 $.
In cartography, in most cases the flattening of the Earth can be ignored or taken into account in one way or another. Therefore, below mappings onto the $ xy $- plane of a spherical surface with respect to the geographical coordinates $ \phi $( latitude) and $ \lambda $( longitude) are considered.
The equation of a map projection has the form
$$ \tag{* } \left . \begin{array}{l} x = f _ {1} ( \phi , \lambda ), \\ y = f _ {2} ( \phi , \lambda ), \\ \end{array} \right \} $$
where $ f _ {1} $ and $ f _ {2} $ are functions satisfying some general conditions. (A map projection can also be defined by equations in which some planar coordinates other than the rectangular ones $ x, y $ are used.) The representations of the meridians $ \lambda = \textrm{ const } $( lines of constant longitude) and the parallels $ \phi = \textrm{ const } $( lines of constant latitude) under a given map projection form a cartographic network (or graticule).
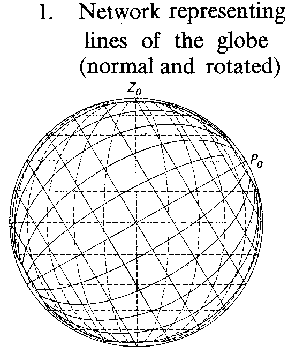
Figure: c020650a
Network representing lines of the globe (normal and rotated)
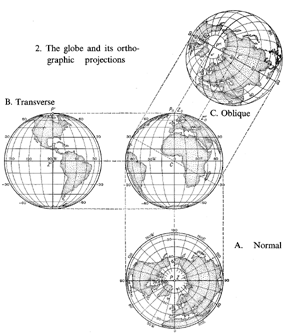
Figure: c020650b
The globe and its orthographic projections A. Normal B. Transverse C. Oblique

Figure: c020650c
Cylindrical projections A. Mercator (conformal) B. Rectangular C. Orthographic (equal area)
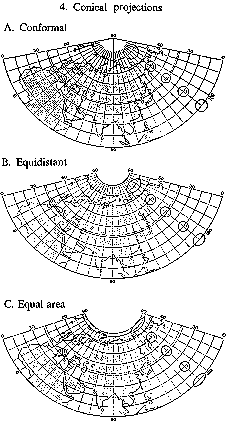
Figure: c020650d
Conical projections A. Conformal B. Equidistant C. Equal area
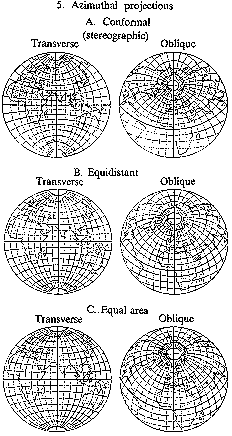
Figure: c020650e
Azimuthal projections A. Conformal (stereographic) Transverse Oblique B. Equidistant Transverse Oblique C. Equal area Transverse Oblique
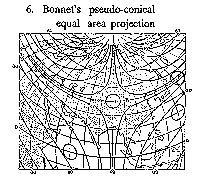
Figure: c020650f
Bonnet's pseudo-conical equal-area projection
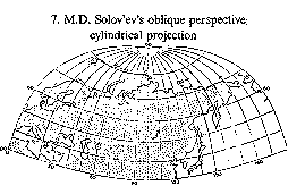
Figure: c020650g
M.D. Solov'ev's oblique perspective cylindrical projection
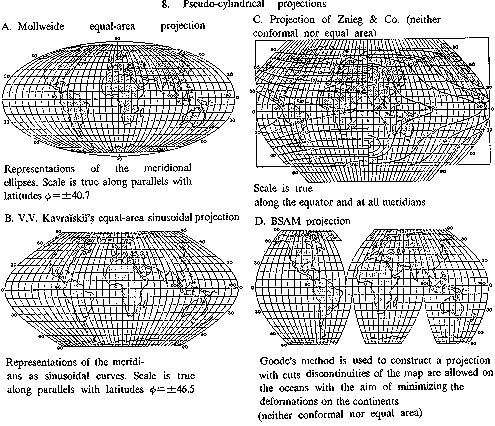
Figure: c020650h
Pseudo-cylindrical projections A. Mollweide equal-area projection Representations of the meridional ellipses. Scale is true along parallels with latitudes $ \phi = \pm 40.7 $ B. V.V. Kavraiskii's equal-area sinusoidal projection Representations of the meridians as sinusoidal curves. Scale is true along parallels with latitudes $ \phi = \pm 46.5 $ C. Projection of Znieg & Co. (neither conformal nor equal area) Scale is true along the equator and at all meridians D. BSAM projection Goode's method is used to construct a projection with cuts: discontinuities of the map are allowed on the oceans with the aim of minimizing the deformations on the continents

Figure: c020650i
9. Poly-conical projections A. Simple Scale is true along each parallel and at the central meridian B. G.A. Ginsburg projection (neither conformal nor equal area) Scale is true along parallels with latitudes $ \phi = \pm 45 $
When mapping some part of the Earth for which the orientation or location is different from that intended for the basic projection, a transformation of the graticule is used. Having a new "north pole" , the projection may be plotted using the original formulas or graphical construction. In Fig. a, $ z _ {0} ( \phi _ {0} , \lambda _ {0} ) $ is the new graphical north pole. A map projection given by equations (*) is called normal or regular $ ( \phi _ {0} = \pi /2) $. If the same projection of the sphere is calculated in terms of the formulas (*), but using $ z, a $ instead of $ \phi , \lambda $, then the projection is called transverse if $ \phi _ {0} = 0 $ and oblique if $ 0 < \phi _ {0} < \pi /2 $. In Fig. b, a normal , transverse (B) and an oblique (C) projection of the sphere are shown.
The distortion in an infinitely small region around some point of the area to be mapped is subject to certain rules. At every point of a map formed by a non-conformal projection (see below) there is a right angle intersection of two lines in some direction which are also shown at right angles on the Earth's surface; these are the so-called principal directions of the mapping. The relative scales along these directions have the extremal values
$$ \left ( { \frac \mu {M} } \right ) _ \max = a \ \textrm{ and } \ \left ( { \frac \mu {M} } \right ) _ \min = b . $$
If in some cartographic projection the images of the meridians and parallels are perpendicular to another, then their directions are principal for the given map projection. The linear distortion at a given point of a map is graphically represented by the ellipse of distortion, which can be regarded as an infinitely small circle on the Earth projected as an infinitely small ellipse under any map projection. For each direction the ellipse shows the corresponding linear distortion or relative scale, the semi-axes of the ellipse are equal to the extremal values of the relative scales and their directions are the principal ones.
Under conformal (or orthomorphic) map projections, the scale depends only on the position of the point and not on the direction. The ellipses of distortion are circles. Examples are the Mercator projections, the stereographic projections, the conformal conical projections, etc. (see Fig. cA, Fig. eA, Fig. dA).
Under equal-area (or equivalent) map projections, areas are preserved; more precisely, areas or figures on maps formed by such projections are proportional to the areas of the original figures, the equal-area coefficient, being the reciprocal of the square of the principal scale of the map, is constant for each map as the result of an equal-area projection. The ellipses of distortion have the same area at all points, but differ in their shape and orientation (see, for example, Fig. cB, Fig. dB, Fig. eB).
Some map projections (see, for example, Fig. g) are neither conformal nor equal area. These can be regarded as a compromise. The equidistant projection showing true scale between one or two points and every other point on the map, or along every meridian (see Fig. cB, Fig. dB, Fig. eB), and the orthodromic ones in which the great circles of the sphere (orthodromes) are represented by straight lines are distinguished among them.
A projection of a sphere onto the plane cannot be conformal, equal area, equidistant, and orthodromic at the same time.
In order to depict the distortion at different positions in the mapped region, one uses: ellipses of distortion (see, for example, Fig. c, Fig. d); isoclines, i.e. lines of true scale (in Fig. hC one can see the isoclines of maximum angular distortion and the isoclines of area change); the images of certain spherical lines, usually orthodromes "O" and isogonal trajectories of meridional loxodromes "L" (see, for example, Fig. cA, Fig. cB).
According to the appearance of the cartographic network, map projections are divided into the following groups.
Cylindrical projections — projections in which meridians are depicted by equidistant parallel straight lines, while the parallels become straight lines perpendicular to the meridians (see Fig. c).
Conical projections — projections in which the parallels are depicted by concentric circles, and the meridians by straight lines orthogonal to them, where the angles between the latter are proportional to the differences of the corresponding longitudes (see Fig. d).
Azimuthal projections — projections in which the parallels are depicted by concentric circles, and the meridians by their radii, where the angles between the latter are equal to the differences of the corresponding longitudes (see Fig. e).
Pseudo-conical projections — projections in which the parallels are depicted by concentric circles, the central meridian by a straight line, and the remaining meridians by curves symmetric with respect to the image of the central meridian (see, for example, Fig. f).
Pseudo-cylindrical projections — projections in which the parallels are depicted by parallel straight lines, the central meridian by a straight line perpendicular to these lines, and the remaining meridians by curves (see Fig. h).
Poly-conical projections — projections in which the parallels are depicted by circles with centres lying on the straight line representing the central meridian, and the remaining meridians by curves which are also symmetric about this straight line (see Fig. i). In the construction of concrete poly-conical projections, extra conditions are imposed.
There also exist projections which are not of the above types. Cylindrical, conical and azimuthal projections, called elementary, often refer to circular projections in the wide sense, selecting from them the circular projections in the narrow sense, that is, projections for which all the meridians and parallels are depicted by circles.
Concerning the use, the choice, the investigation of properties concerning transformations realized by map projections, see Cartography, mathematical problems in and the literature cited therein.
Comments
Some comments on the cartographic projections:
8B) V.V. Kavraiskii's equal-area projection is almost identical to the Eckert VI projection. The poles are half the length of the equator; the meridians are sinusoidal curves.
8D) BSAM projection. The letters BSAM stand for Bolshoi Sovetskii Atlas Mira (the Great Soviet World Atlas), first published in 1937. In that atlas the projection given here is called the interrupted sinusoidal projection.
9B) The Russians have made various modifications of the poly-conical projection in order to reduce scale exaggeration along meridians near the edge of the graticule.
The ellipse of distortion is also called Tissot's indicatrix (see also Cartography, mathematical problems in), after N.A. Tissot who in 1859 first published his classic analysis of the distortion occurring under a map projection.
A loxodrome, or rumb line, is a line of constant direction on a sphere. For orthodrome see Cartography, mathematical problems in.
References
| [a1] | J.P. Snyder, "Map projections - a working manual" , U.S. Geol. Survey , 1393 , U.S. Government Printing Office (1987) |
Cartographic projection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cartographic_projection&oldid=53341