Bessel functions
2020 Mathematics Subject Classification: Primary: 33C10 [MSN][ZBL]
Some authors use this term for all the cylinder functions. In this entry the term is used for the cylinder functions of the first kind (which are usually called Bessel functions of the first kind by those authors which use the term Bessel functions for all cylinder functions). For the Bessel functions of the second kind, denoted by $Y_\nu$ (more rarely by $N_\nu$) and also called Neumann functions or Weber functions, see Cylinder functions and Neumann function. For the Bessel functions of the third kind see Cylinder functions and Hankel functions.
Definition
The Bessel function of order $\nu \in \mathbb C$ can be defined, when $\nu$ is not a negative integer, via the series \begin{equation}\label{e:series} J_\nu (z) := \sum_{k=0}^\infty \frac{(-1)^k}{\Gamma (k+1) \Gamma (k+\nu+1)} \left(\frac{z}{2}\right)^{\nu + 2k} = \left(\frac{z}{2}\right)^\nu \sum_{k=0}^\infty \frac{(-1)^k}{\Gamma (k+1) \Gamma (k+\nu+1)} \left(\frac{z}{2}\right)^{2k}\, , \end{equation} where $\Gamma$ is the Gamma-function. The series in the second identity converges on the entire complex plane (when $\nu$ is not a negative integer) and hence the indeterminacy (or multi-valued nature) in the analytic function $J_\nu$ is reduced to that of $z^\nu$ when $\nu\not \in \mathbb N$. When $\nu = n \in \mathbb N$, the Bessel function is therefore entire and the Taylor series in \eqref{e:series} takes the simple form \[ J_n (z) = \left(\frac{z}{2}\right)^n \sum_{k=0}^\infty \frac{(-1)^k}{k!(n+k)!} \left(\frac{z}{2}\right)^{2k}\, . \] When $\nu = -n$ with $n\in \mathbb N$, the formulas in \eqref{e:series} are not "strictly speaking" well-defined because the $\Gamma$ function has poles in all negative integers. However, given the Laurent series of $\Gamma$ at such poles and the fact that the function appears in the denominators of fractions, the formula \eqref{e:series} can be intepreted, for $\nu = -n$ as \[ J_{-n} (z) = \left(\frac{z}{2}\right)^{-n} \sum_{k=0}^\infty \frac{(-1)^{n+k}}{k!(n+k)!} \left(\frac{z}{2}\right)^{2k+2n} = (-1)^n J_n (z)\, . \]
Real and integer order
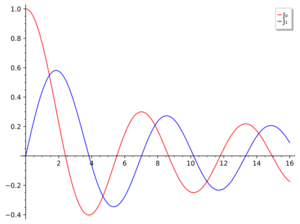
If the argument is real and the order $\nu$ is integer, the Bessel function is real, and its graph has the form of a damped vibration (Fig. 1). If the order is even, the Bessel function is even, if odd, it is odd. If $\nu$ is real and the argument is real, it is a common convention to take the determination of $z^\nu$ which takes real values for positive real values of $z$. Thus the Bessel function $J_\nu$ is real on the positive real axis when $\nu\in \mathbb R$.
The behaviour of a Bessel function $J_n$ for $n$ integer in a neighbourhood of zero is given by the first term of the series \eqref{e:series}; for large $z$, $|{\arg z}|<\pi$, the asymptotic representation \[ J_n (z) = \sqrt{\frac{2}{\pi z}} \cos \left(z - \frac{\pi}{2} n - \frac{\pi}{4}\right) +O\left(\frac{1}{z}\right) \] (which holds also for real or complex $\nu$).
The zeros of a Bessel function $J_\nu$ with $\nu \in \mathbb R$ (i.e. the roots of the equation $J_\nu (x) =0$) are simple, and the zeros of $J_\nu$ are situated between the zeros of $J_{\nu+1}$.
Half integer order
Bessel functions of "half-integral" order $\nu = n+ \frac{1}{2}$ with $n\in \mathbb Z$ can be expressed by trigonometric functions; in particular we have \[ J_{1/2} (x) = \sqrt{\frac{2}{\pi x}} \sin x \qquad J_{-1/2} (x) = \sqrt{\frac{2}{\pi x}} \cos x\, . \] More in general there are polynomials $P_n$ and $Q_n$, for $n\in \mathbb N$, with \begin{eqnarray*} && \deg P_n = \deg Q_n = n\\ && P_n (-x) = (-1)^n P_n (x) \qquad Q_n (-x) = (-1)^n Q_n (x) \end{eqnarray*} such that \begin{eqnarray} &&J_{n+1/2} (x) = \sqrt{\frac{2}{\pi x}} \left(P_n \left(\frac{1}{x}\right) \sin x - Q_{n-1} \left(\frac{1}{x}\right) \cos x \right)\\ &&J_{-n-1/2} (x) = (-1)^n \sqrt{\frac{2}{\pi x}} \left(P_n \left(\frac{1}{x}\right) \cos x + Q_{n-1} \left(\frac{1}{x}\right) \sin x \right)\, . \end{eqnarray}
Fourier-Bessel series
Let $\nu$ be real larger than $-\frac{1}{2}$ and denote by $\mu_n^\nu$ the positive zeros of $J_\nu$. Then the functions $x \mapsto b_n (x) := J_\nu (\mu_n^\nu x)$, $n\in \mathbb N\setminus \{0\}$ form an orthogonal system with weight $x$ in the interval $[0,1]$. Under certain conditions the following expansion, called Fourier-Bessel series, is then valid: \[ f(x) = \sum_{n=1}^\infty c_n b_n (x) \] where \[ c_n = \frac{2}{(J_{\nu+1} (\mu_n^\nu))} \int_0^1 x\, f (x)\, b_n (x)\, dx\, . \] On the infinite half-line $[0, \infty[$ this expansion is replaced by the Fourier–Bessel integral: \[ f(x) = \int_0^\infty c (\lambda)\, J_\nu (\lambda x)\, d\lambda \] where \[ c (\lambda) = \int J_\nu (\lambda x)\, f(x)\, x\, dx\, . \]
Notable formulas
The following formulas play an important role in the theory of Bessel functions and their applications:
1) The integral representation, which for $n$ integer takes the form \[ J_n (z) = \frac{1}{\pi} \int_0^\pi \cos\, (z \sin \phi - n \phi)\, d \phi \] and was the starting point of Bessel himself in his original investigations. For $\nu$ complex and ${\rm Re}\, z > 0$ the identity can be extended as \[ J_\nu (z) = \frac{1}{\pi} \int_0^\pi \cos\, (z \sin \phi - \nu \phi)\, d \phi - \frac{\sin (\pi \nu)}{\pi} \int_0^\infty e^{-z \sinh t - \nu t}\, dt\, . \]
2) The generating function \[ e^{z\, (\xi - \xi^{-1})/2} = \sum_{k=-\infty}^\infty J_k (z)\, \xi^k\, . \]
3) The addition theorem for integer order $n\in \mathbb Z$ \[ J_n (z_1+z_2) = \sum_{k=-\infty}^\infty J_k (z_1)\, J_{n-k} (z_2)\, . \]
4) The recurrence formulas \begin{eqnarray*} && J_{\nu-1} (z) + J_{\nu+1} (z) = \frac{2\nu}{z} J_\nu (z)\\ && J'_\nu (z) = \frac{1}{2} (J_{\nu-1} (z) - J_{\nu+1} (z))\, . \end{eqnarray*}
References
- [Co] H. Cohen, "Number theory volume II: analytic and modern tools", Springer (2007) Zbl 1119.11002
- [GR] I. S. Gradshteyn, I. M. Ryzhik, "Table of integrals, series and products", Academic Press (2000)
- [Wa] G. N. Watson, "A Treatise on the Theory of Bessel Functions", Cambridge University Press (1922)
Bessel functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bessel_functions&oldid=56053