Baric algebra

weighted algebra

In 1939, in connection with the formalism of genetics, I.M.H. Etherington introduced the notion of baric algebra (cf. [a1]; more commonly it is also called a weighted algebra). If 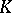is a (commutative) field and 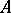a -a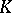lgebra, not necessarily commutative or associative, one says that 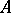is a weighted algebra if there exists an algebra morphism 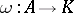which is non-trivial. This means that one can write 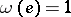, where is a convenient element of 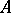. The morphism 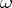is called the weight function of 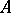and one can regard a weighted algebra as a pair 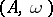where 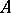is an algebra and 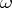the weight function. A morphism 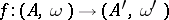of weighted algebras is a morphism of algebras 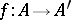such that 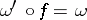. This gives a category, the category of weighted algebras. All constructions on weighted algebras are made in this category. For a finite-dimensional 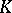-algebra 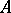, the following conditions are equivalent:

i) 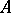is a weighted algebra;

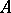ii) there exists a finite basis of over 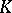such that if 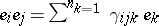(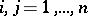) is the multiplication table of 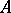in this basis (the scalars 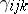(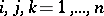) are the structure constants of 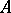), then ();

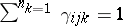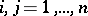iii) there exists a two-sided ideal 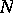of 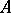, of codimension one, such that .

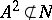It is easy to see that a Lie algebra is not weighted; however, over any weighted algebra 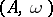one can define a Lie algebra structure via the multiplication (bracket) 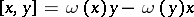for all 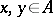. A Jordan algebra may or may not be weighted; however, over any weighted algebra 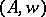one can define a Jordan algebra structure via the multiplication 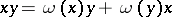for all 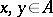. A weighted algebra is not necessarily associative (cf. Associative rings and algebras); however, over any weighted algebra 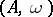with a unit one can define an associative algebra structure via the multiplication 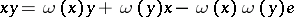for all 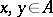. A Clifford algebra is not weighted; in particular, the algebra of complex numbers and the algebra of quaternions are not weighted. All Bernstein algebras are weighted (cf. Bernstein algebra).

References

[a1]	I.M.H. Etherington, "Genetic algebras" Proc. Roy. Soc. Edinburgh , 59 (1939) pp. 242–258
[a2]	D. McHale, G.A. Ringwood, "Haldane linearisation of baric algebras" J. London Math. Soc. (2) , 28 (1983) pp. 17–26
[a3]	A. Micali, Ph. Revoy, "Sur les algèbres gamétiques" Proc. Edinburgh Math. Soc , 29 (1986) pp. 187–197
[a4]	M.K. Singh, D.K. Singh, "On baric algebras" The Math. Education (2) , 20 (1986) pp. 54–55