Banach function algebra
A Banach algebra of continuous functions on a compact Hausdorff space 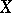 separating the points of
separating the points of 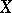 and containing the constant functions (cf. also Algebra of functions). One speaks of a real or complex Banach function algebra according to whether the functions are real- or complex-valued. If the Banach algebra norm is the supremum norm, one speaks of a function algebra (or a uniform algebra). An example of a Banach function algebra which is not a uniform algebra is the algebra of all real- (or complex-) valued continuously differentiable functions on the unit interval
and containing the constant functions (cf. also Algebra of functions). One speaks of a real or complex Banach function algebra according to whether the functions are real- or complex-valued. If the Banach algebra norm is the supremum norm, one speaks of a function algebra (or a uniform algebra). An example of a Banach function algebra which is not a uniform algebra is the algebra of all real- (or complex-) valued continuously differentiable functions on the unit interval 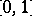 with norm given by
with norm given by
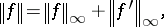 |
where 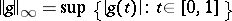 for a continuous function
for a continuous function 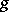 on the interval
on the interval 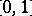 . See, e.g., [a1], [a2].
. See, e.g., [a1], [a2].
Let 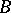 be a commutative semi-simple Banach algebra with unit and let
be a commutative semi-simple Banach algebra with unit and let 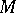 be the maximal ideal space (cf. also Commutative Banach algebra) for
be the maximal ideal space (cf. also Commutative Banach algebra) for 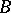 . One can identify the elements of
. One can identify the elements of 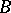 with continuous functions on the compact Hausdorff space
with continuous functions on the compact Hausdorff space 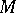 via the Gel'fand transform and then
via the Gel'fand transform and then 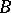 is a Banach function algebra on
is a Banach function algebra on 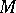 . More generally, if
. More generally, if 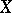 is a compact subset of
is a compact subset of 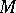 such that the
such that the  -element of
-element of 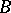 is the only function in
is the only function in 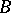 vanishing on
vanishing on 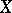 , then the restriction to
, then the restriction to 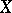 of the functions in
of the functions in 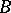 is a Banach function algebra on
is a Banach function algebra on 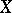 . Conversely, if
. Conversely, if 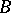 is a Banach function algebra on
is a Banach function algebra on 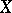 , then
, then 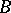 is a semi-simple commutative Banach algebra, and
is a semi-simple commutative Banach algebra, and 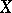 can be imbedded in the maximal ideal space for
can be imbedded in the maximal ideal space for 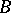 via the mapping that sends a point of
via the mapping that sends a point of 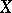 to the evaluation functional at that point.
to the evaluation functional at that point.
There is the following characterization of 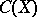 , the algebra of all real-valued continuous functions on a compact Hausdorff space
, the algebra of all real-valued continuous functions on a compact Hausdorff space 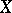 , among the real Banach function algebras: If
, among the real Banach function algebras: If 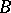 is a Banach function algebra on
is a Banach function algebra on 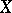 and if there is a number
and if there is a number 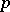 between 0 and 1 such that
between 0 and 1 such that 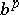 is in
is in 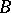 whenever
whenever 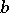 is in
is in 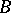 and
and 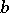 is non-negative on
is non-negative on 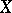 , then
, then 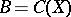 , see [a2], [a3].
, see [a2], [a3].
References
| [a1] | R.B. Burckel, "Characterizations of 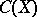 among its subalgebras" , M. Dekker (1972) among its subalgebras" , M. Dekker (1972) |
| [a2] | O. Hatori, "Symbolic calculus on a Banach algebra of continuous functions" J. Funct. Anal. , 115 (1993) pp. 247–280 |
| [a3] | Y. Katznelson, "Sur les algèbres dont les éléments non-négatifs admettent des racines carrés" Ann. Sci. École Norm. Sup. , 77 (1960) pp. 167–174 |
Banach function algebra. E. Briem (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Banach_function_algebra&oldid=15556