Ball
A set  of points
of points  in a Euclidean space
in a Euclidean space  at a distance from a given point
at a distance from a given point  (the centre of the ball) less than (an open ball
(the centre of the ball) less than (an open ball  ), or not greater than (a closed ball
), or not greater than (a closed ball  ) a quantity
) a quantity  (the radius of the ball), i.e.
(the radius of the ball), i.e.
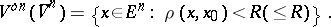 |
A ball  is a line segment,
is a line segment, 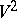 is a disc,
is a disc,  for
for 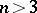 is sometimes called a hyperball. The boundary (surface) of a ball is a sphere.
is sometimes called a hyperball. The boundary (surface) of a ball is a sphere.
The volume of a ball is
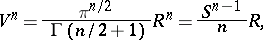 |
where 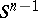 is the surface of the boundary sphere and
is the surface of the boundary sphere and 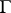 is the gamma-function:
is the gamma-function: 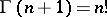 ,
, 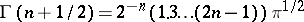 . In particular,
. In particular,
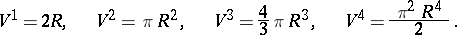 |
With the increase of the dimension, the volume of a ball "concentrates" at its surface:
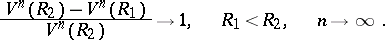 |
A ball is the simplest geometrical figure. Its topology is trivial. Among all bodies of an equal volume, a ball has minimal surface, and among all bodies of an equal surface, it has maximal volume.
In exactly the same manner a ball can be defined in a metric space; however, in this case it need not be, for example, strictly convex, its surface may have non-smooth points, etc., that is, it may have all phenomena characteristic of arbitrary convex bodies.
Unlike a finite-dimensional ball, an infinite-dimensional ball, being the direct limit of a sequence of balls of successive dimensions imbedded in one another, does not have a compact closure. On the contrary, the compactness of a ball in a topological vector space indicates the finite dimensionality of the latter.
For references, see Sphere.
Ball. I.S. Sharadze (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ball&oldid=16703