Auto-regressive process
A stochastic process  whose values satisfy an auto-regression equation with certain constants
whose values satisfy an auto-regression equation with certain constants  :
:
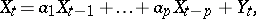 | (*) |
where  is some positive number and where the variables
is some positive number and where the variables  are usually assumed to be uncorrelated and identically distributed around their average value 0 with a variance
are usually assumed to be uncorrelated and identically distributed around their average value 0 with a variance  . If all the zeros of the function
. If all the zeros of the function  of a complex variable
of a complex variable  lie inside the unit circle, then equation (*) has the solution
lie inside the unit circle, then equation (*) has the solution
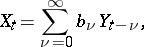 |
where the  are connected with the
are connected with the 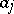 by the relation
by the relation
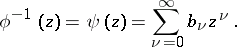 |
For example, let 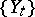 be a white noise process with spectral density
be a white noise process with spectral density 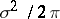 ; in such a case the only kind of auto-regressive process satisfying equation (*) will be a process
; in such a case the only kind of auto-regressive process satisfying equation (*) will be a process 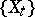 with spectral density
with spectral density
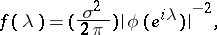 |
which is stationary in the wide sense if  has no real zeros. The autocovariances (cf. Autocovariance)
has no real zeros. The autocovariances (cf. Autocovariance)  of the process satisfy the recurrence relation
of the process satisfy the recurrence relation
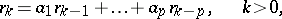 |
and, in terms of the 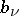 , have the form
, have the form
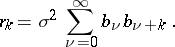 |
The parameters 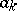 of the auto-regression are connected with the auto-correlation coefficients
of the auto-regression are connected with the auto-correlation coefficients 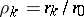 of the process by the matrix relation
of the process by the matrix relation
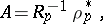 |
where  ,
, 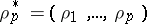 and
and 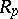 is the matrix of auto-correlation coefficients (the Yule–Walker equation).
is the matrix of auto-correlation coefficients (the Yule–Walker equation).
References
| [1] | U. Grenander, M. Rosenblatt, "Statistical analysis of stationary time series" , Wiley (1957) |
| [2] | E.J. Hannan, "Time series analysis" , Methuen , London (1960) |
Auto-regressive process. A.V. Prokhorov (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Auto-regressive_process&oldid=15186