Analytic continuation into a domain of a function given on part of the boundary
The following classical assertion is well known. Let $D \subset \mathbf{C}$ be a simply connected bounded domain with smooth boundary $\partial D$, and $f \in C ( \partial D )$. Then
\begin{equation} \tag{a1} \int _ { \partial D } f z _ { 1 } ^ { m } d z _ { 1 } = 0 , \quad m = 0,1 , \dots , \end{equation}
if and only if $f ( z )$ extends into the domain $D$ as a holomorphic function of the class $H ( D ) \cap C ( \overline { D } )$. For the multi-dimensional case $D \subset \mathbf{C} ^ { x }$, instead of the form $z _ { 1 } ^ { m } d z _ { 1 }$, one takes an exterior differential form of class $Z _ { n , n - 1 } ^ { \infty } ( \overline { D } )$.
If $f$ is defined only on a part of the boundary of $D$, then the existence of an analytic continuation into $D$ cannot be decided by the vanishing of some family of continuous linear functionals as in (a1). Solutions to this problem were given from the 1950s onwards by many mathematicians, see, e.g. [a1], [a2].
Some very simple solutions are given below.
1) $n = 1$. Let $D$ be the domain bounded by a part of the unit circle $\gamma = \{ z _ { 1 } : | z _ { 1 } | = 1 \}$ and a smooth open arc $\Gamma$ connecting two points of $\gamma$ and lying inside $\gamma$. Let $0 \notin \overline { D }$. Set
\begin{equation*} a _ { k } = \int _ { \Gamma } \frac { f ( \zeta ) d \zeta } { \zeta ^ { k + 1 } } , \quad k = 0,1, \dots . \end{equation*}
Then the following assertion holds: If $f \in C ( \Gamma ) \cap L ^ { 1 } ( \Gamma )$, then there is a function $F \in H ( D ) \cap C ( D \cup \Gamma )$ such that $F | _ { \Gamma } = f$ if and only if
\begin{equation} \tag{a2} \operatorname { limsup } _ { k \rightarrow \infty } \sqrt [ | a _k |] {k}\leq 1 \end{equation}
If $f | _ { \Gamma }$ is not identically zero, then (a2) is equivalent to
\begin{equation*} \limsup _ { k \rightarrow \infty } \sqrt [ |a_{ k } | ] { k } = 1. \end{equation*}
2) $n > 1$. Let $\Omega = \{ \zeta : \psi ( \zeta ) < 0 \}$ be a $( p _ { 1 } , \dots , p _ { n } )$-circular convex domain in $\mathbf{C} ^ { n }$, where $p _ { 1 } , \dots , p _ { n }$ are natural numbers, i.e., $z \in \Omega$ implies $( z _ { 1 } e ^ { i t p _ { 1 } } 1 , \ldots , z _ { n } e ^ { i t p _ { n } } ) \in \Omega$ for $t \in \mathbf{R}$. In particular, for $p _ { 1 } = \ldots = p _ { n } = 1$ this circular domain is a Cartan domain. Moreover, assume that $\Omega$ is convex and bounded and $\partial \Omega \in C ^ { 2 }$. Furthermore, let $D$ be the domain bounded by a part of $\partial \Omega$ and a hyper-surface $\Gamma \in C ^ { 2 }$ dividing $\Omega$ into two parts and assume that the complement of $\overline{ D }$ contains the origin. Consider the Cauchy–Fantappié differential form
\begin{equation*} \operatorname{CF} ( \zeta - z , w ) = \frac { ( n - 1 ) ! \sum _ { k = 1 } ^ { n } ( - 1 ) ^ { k - 1 } w _ { k } d w [ k ] \wedge d \zeta } { \langle w , \zeta - z \rangle ^ { n } }, \end{equation*}
where $d w [ k ] = d w _ { 1 } \wedge \ldots \wedge d w _ { k - 1 } \wedge d w _ { k + 1 } \wedge \ldots \wedge d w _ { n }$, $d \zeta = d \zeta _ { 1 } \wedge \ldots \wedge d \zeta _ { n }$, $\langle a , b \rangle = a _ { 1 } b _ { 1 } + \ldots + a _ { n } b _ { n }$. Then $\operatorname { grad } \psi = ( \partial \psi / \partial \zeta _ { 1 } , \dots , \partial \psi / \partial \zeta _ { n } )$. By the Sard theorem, $\operatorname{grad} \psi \neq 0$ for almost all $r$ on $\partial \Omega _ { r }$, where $\Omega _ { r } = r \Omega$ is the homothetic transform of $\Omega$. Assume that $\operatorname{grad} \psi \neq 0$ on $\Gamma$ and set
\begin{equation*} c _ { q } = \frac { ( | q | + n - 1 ) ! } { q _ { 1 } ! \ldots q _ { n } ! } \times \end{equation*}
\begin{equation*} \times \int _ { \Gamma } f ( \zeta ) \left( \frac { \operatorname { grad } \psi } { ( \operatorname { grad } \psi , \zeta ) } \right) ^ { q } \operatorname {CF} ( \zeta , \operatorname { grad } \psi ), \end{equation*}
where $q = ( q _ { 1 } , \dots , q _ { n } )$, $| q | = q _1 + \ldots + q_n$, $w ^ { q } = w _ { 1 } ^ { q _ { 1 } } \ldots w _ { n } ^ { q _ { n } }$. Let
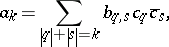 |
where $b _ { q , s } = \int _{\Omega} z ^{q} \overline{z} ^ { s } d v$ and $d v$ is the volume element in $\Omega$. Here, all $q_j$ and $s _ { j }$ are non-negative integers. Note that the integral moments $c _ { q }$ depend on $f$ and $\Gamma$, but the moments $b _ { q ,\, s }$ depend only on $\Omega$.
The following assertion now holds: For a function $f \in C ( \Gamma ) \cap L ^ { 1 } ( \Gamma )$ to have an analytic continuation $F \in H ( D ) \cap C ( D \cup \Gamma )$ with $F | _ { \Gamma } = f$, it is necessary and sufficient that the following two conditions are fulfilled:
i) $f$ is a $C R$-function on $\Gamma$;
ii) $\limsup_{k \rightarrow \infty} \sqrt [ a _ { k } ] { k } \leq 1$.
A consequence of this is as follows. Let $\Omega \subset {\bf C} ^ { n }$ be a bounded convex $n$-circular domain (a Reinhardt domain). Set $d _ { q } ( \Omega ) = \operatorname { max } _ { \overline{\Omega} } | z ^ { q } |$. For a function $f \in C ( \Gamma ) \cap L ^ { 1 } ( \Gamma )$ to have an analytic continuation in $D$ as above it is necessary and sufficient that:
a) $f$ is a $C R$-function on $\Gamma$;
b) $\operatorname { lim}\operatorname { sup}_{| q | \rightarrow \infty} \sqrt[ |c _ { q } | d _ { q } ( \Omega ) ] { | q | } \leq 1$.
References
| [a1] | L. Aizenberg, "Carleman's formulas in complex analysis" , Kluwer Acad. Publ. (1993) |
| [a2] | L. Aizenberg, "Carleman's formulas and conditions of analytic extendability" , Topics in Complex Analysis , Banach Centre Publ. , 31 , Banach Centre (1995) pp. 27–34 |
Analytic continuation into a domain of a function given on part of the boundary. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Analytic_continuation_into_a_domain_of_a_function_given_on_part_of_the_boundary&oldid=50677