Rational function
A rational function is a function  , where
, where  is rational expression in
is rational expression in  , i.e. an expression obtained from an independent variable
, i.e. an expression obtained from an independent variable  and some finite set of numbers (real or complex) by means of a finite number of arithmetical operations. A rational function can be written (non-uniquely) in the form
and some finite set of numbers (real or complex) by means of a finite number of arithmetical operations. A rational function can be written (non-uniquely) in the form
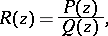 |
where  ,
,  are polynomials,
are polynomials,  . The coefficients of these polynomials are called the coefficients of the rational function. The function
. The coefficients of these polynomials are called the coefficients of the rational function. The function  is called irreducible when
is called irreducible when  and
and  have no common zeros (that is,
have no common zeros (that is,  and
and 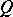 are relatively prime polynomials). Every rational function can be written as an irreducible fraction
are relatively prime polynomials). Every rational function can be written as an irreducible fraction  ; if
; if  has degree
has degree  and
and  has degree
has degree  , then the degree of
, then the degree of  is either taken to be the pair
is either taken to be the pair 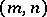 or the number
or the number
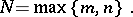 |
A rational function of degree 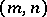 with
with  , that is, a polynomial, is also called an entire rational function. Otherwise it is called a fractional-rational function. The degree of the rational function
, that is, a polynomial, is also called an entire rational function. Otherwise it is called a fractional-rational function. The degree of the rational function 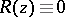 is not defined. When
is not defined. When 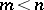 , the fraction
, the fraction 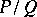 is called proper, and it is called improper otherwise. An improper fraction can be uniquely written as
is called proper, and it is called improper otherwise. An improper fraction can be uniquely written as
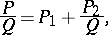 |
where  is a polynomial, called the integral part of the fraction
is a polynomial, called the integral part of the fraction 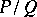 , and
, and  is a proper fraction. A proper fraction,
is a proper fraction. A proper fraction,  , in irreducible form, where
, in irreducible form, where
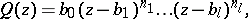 |
admits a unique expansion as a sum of simple partial fractions
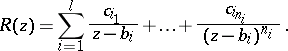 | (1) |
If  is a proper rational function with real coefficients and
is a proper rational function with real coefficients and
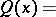 |
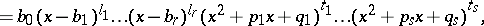 |
where 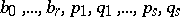 are real numbers such that
are real numbers such that  for
for 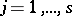 , then
, then 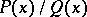 can be uniquely written in the form
can be uniquely written in the form
 | (2) |
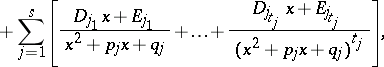 |
where all the coefficients are real. These coefficients, like the 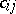 in (1), can be found by the method of indefinite coefficients (cf. Undetermined coefficients, method of).
in (1), can be found by the method of indefinite coefficients (cf. Undetermined coefficients, method of).
A rational function of degree  in irreducible form is defined and analytic in the extended complex plane (that is, the plane together with the point
in irreducible form is defined and analytic in the extended complex plane (that is, the plane together with the point  ), except at a finite number of singular points, poles: the zeros of its denominator and, when
), except at a finite number of singular points, poles: the zeros of its denominator and, when 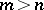 , also the point
, also the point 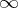 . Note that if
. Note that if 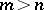 , the sum of the multiplicities of the poles of
, the sum of the multiplicities of the poles of  is equal to its degree
is equal to its degree 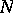 . Conversely, if
. Conversely, if 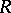 is an analytic function whose only singular points in the extended complex plane are finitely many poles, then
is an analytic function whose only singular points in the extended complex plane are finitely many poles, then  is a rational function.
is a rational function.
The application of arithmetical operations (with the exception of division by 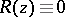 ) to rational functions again gives a rational function, so that the set of all rational functions forms a field. In general, the rational functions with coefficients in a field form a field. If
) to rational functions again gives a rational function, so that the set of all rational functions forms a field. In general, the rational functions with coefficients in a field form a field. If 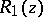 ,
, 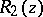 are rational functions, then
are rational functions, then  is also a rational function. The derivative of order
is also a rational function. The derivative of order 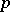 of a rational function of degree
of a rational function of degree 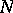 is a rational function of degree at most
is a rational function of degree at most  . An indefinite integral (or primitive) of a rational function is the sum of a rational function and expressions of the form
. An indefinite integral (or primitive) of a rational function is the sum of a rational function and expressions of the form 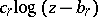 . If a rational function
. If a rational function  is real for all real
is real for all real  , then the indefinite integral
, then the indefinite integral  can be written as the sum of a rational function
can be written as the sum of a rational function 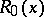 with real coefficients, expressions of the form
with real coefficients, expressions of the form
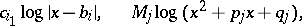 |
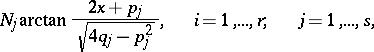 |
and an arbitrary constant  (where
(where  ,
, 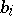 ,
, 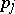 ,
,  are the same as in (2), and
are the same as in (2), and  ,
, 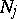 are real numbers). The function
are real numbers). The function  can be found by the Ostrogradski method, which avoids the need to expand
can be found by the Ostrogradski method, which avoids the need to expand 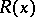 into partial fractions (2).
into partial fractions (2).
For ease of computation, rational functions can be used to approximate a given function. Attention has also been paid to rational functions  in several real or complex variables, where
in several real or complex variables, where  and
and  are polynomials in these variables with
are polynomials in these variables with  , and to abstract rational functions
, and to abstract rational functions
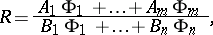 |
where 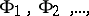 are linearly independent functions on some compact space
are linearly independent functions on some compact space  , and
, and  are numbers. See also Fractional-linear function; Zhukovskii function.
are numbers. See also Fractional-linear function; Zhukovskii function.
References
| [1] | I.I. [I.I. Privalov] Priwalow, "Einführung in die Funktionentheorie" , 1–3 , Teubner (1958–1959) (Translated from Russian) |
| [2] | A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian) |
Comments
For approximation results see Padé approximation.
References
| [a1] | J.B. Conway, "Functions of one complex variable" , Springer (1973) |
| [a2] | S. Lang, "Algebra" , Addison-Wesley (1984) |
Rational functions on an algebraic variety are a generalization of the classical concept of a rational function (see section 1)). A rational function on an irreducible algebraic variety  is an equivalence class of pairs
is an equivalence class of pairs  , where
, where  is a non-empty open subset of
is a non-empty open subset of  and
and  is a regular function on
is a regular function on  . Two pairs
. Two pairs 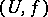 and
and 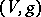 are said to be equivalent if
are said to be equivalent if  on
on  . The rational functions on
. The rational functions on 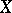 form a field, denoted by
form a field, denoted by  .
.
In the case when  is an irreducible affine variety, the field of rational functions on
is an irreducible affine variety, the field of rational functions on  coincides with the field of fractions of the ring
coincides with the field of fractions of the ring  . The transcendence degree of
. The transcendence degree of  over
over  is called the dimension of the variety
is called the dimension of the variety  .
.
References
| [1] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
Vik.S. Kulikov
Rational function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rational_function&oldid=17805