The polynomials 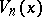 (cf. [a1] and [a5]) given by
(cf. [a1] and [a5]) given by
 | (a1) |
They reduce to the Lucas numbers 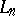 for
for 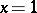 , and they satisfy several identities, which may be easily proved by induction, e.g.:
, and they satisfy several identities, which may be easily proved by induction, e.g.:
 | (a2) |
 | (a3) |
 | (a4) |
 | (a5) |
 | (a6) |
where 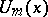 denote the Fibonacci polynomials;
denote the Fibonacci polynomials;
 | (a7) |
where
so that 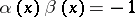 ; and
; and
 | (a8) |
where 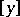 denotes the greatest integer in
denotes the greatest integer in 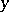 .
.
The Lucas polynomials are related to the Chebyshev polynomials 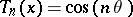 ,
, 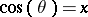 , by
, by
 | (a9) |
J. Riordan [a9] considered the polynomials 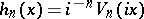 and the Lucas-type polynomials
and the Lucas-type polynomials
 | (a10) |
in a derivation of Chebyshev-type pairs of inverse relations. V.E. Hoggatt Jr. and M. Bicknell [a4] found the roots of 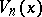 . These are
. These are 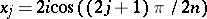 ,
, 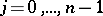 . Bicknell [a2] showed that
. Bicknell [a2] showed that 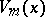 divides
divides  if and only if
if and only if  is an odd multiple of
is an odd multiple of 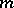 . G.E. Bergum and Hoggatt Jr. introduced in [a1] the bivariate Lucas polynomials
. G.E. Bergum and Hoggatt Jr. introduced in [a1] the bivariate Lucas polynomials 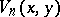 by the recursion
by the recursion
 | (a11) |
generalized (a7) for 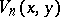 , and showed that the
, and showed that the 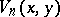 are irreducible polynomials over the rational numbers if and only if
are irreducible polynomials over the rational numbers if and only if 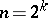 for some positive integer (cf. also Irreducible polynomial). The formula
for some positive integer (cf. also Irreducible polynomial). The formula
 | (a12) |
which may be derived by induction on  or by expanding the generating function of
or by expanding the generating function of 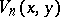 , generalizes (a8).
, generalizes (a8).
Ch.A. Charalambides [a3] introduced and studied the Lucas and Lucas-type polynomials of order 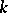 ,
, 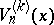 and
and 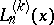 . The Lucas-type polynomials of order
. The Lucas-type polynomials of order 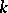 satisfy the recurrence
satisfy the recurrence
 | (a13) |
These polynomials have the binomial and multinomial expansions
 | (a14) |
where the second summation is taken over all non-negative integers  such that
such that 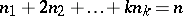 , and they are related to the Fibonacci-type polynomials of order
, and they are related to the Fibonacci-type polynomials of order 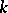 (cf. [a6] and [a8] and Fibonacci polynomials),
(cf. [a6] and [a8] and Fibonacci polynomials), 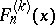 , by
, by
 | (a15) |
Furthermore,
 | (a16) |
where the 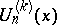 are the Fibonacci polynomials of order
are the Fibonacci polynomials of order 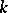 (cf. [a7]). Charalambides [a3] showed that the reliability of a circular consecutive
(cf. [a7]). Charalambides [a3] showed that the reliability of a circular consecutive 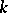 -out-of-
-out-of- :
:  -system,
-system, 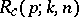 , whose components function independently with probability
, whose components function independently with probability 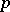 is given by
is given by
 | (a17) |
References
| [a1] | G.E. Bergum, V.E. Hoggatt, Jr., "Irreducibility of Lucas and generalized Lucas polynomials" Fibonacci Quart. , 12 (1974) pp. 95–100 |
| [a2] | M. Bicknell, "A primer for the Fibonacci numbers VII" Fibonacci Quart. , 8 (1970) pp. 407–420 |
| [a3] | Ch.A. Charalambides, "Lucas numbers and polynomials of order 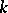 and the length of the longest circular success run" Fibonacci Quart. , 29 (1991) pp. 290–297 and the length of the longest circular success run" Fibonacci Quart. , 29 (1991) pp. 290–297 |
| [a4] | V.E. Hoggatt Jr., M. Bicknell, "Roots of Fibonacci polynomials" Fibonacci Quart. , 11 (1973) pp. 271–274 |
| [a5] | E. Lucas, "Theorie de fonctions numeriques simplement periodiques" Amer. J. Math. , 1 (1878) pp. 184–240; 289–321 |
| [a6] | A.N. Philippou, "Distributions and Fibonacci polynomials of order 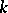 , longest runs, and reliability of consecutive- , longest runs, and reliability of consecutive-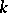 -out-of- -out-of- : : 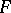 systems" A.N. Philippou (ed.) G.E. Bergum (ed.) A.F. Horadam (ed.) , Fibonacci Numbers and Their Applications , Reidel (1986) pp. 203–227 systems" A.N. Philippou (ed.) G.E. Bergum (ed.) A.F. Horadam (ed.) , Fibonacci Numbers and Their Applications , Reidel (1986) pp. 203–227 |
| [a7] | A.N. Philippou, C. Georghiou, G.N. Philippou, "Fibonacci polynomials of order 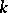 , multinomial expansions and probability" Internat. J. Math. Math. Sci. , 6 (1983) pp. 545–550 , multinomial expansions and probability" Internat. J. Math. Math. Sci. , 6 (1983) pp. 545–550 |
| [a8] | A.N. Philippou, C. Georghiou, G.N. Philippou, "Fibonacci-type polynomials of order 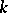 with probability applications" Fibonacci Quart. , 23 (1985) pp. 100–105 with probability applications" Fibonacci Quart. , 23 (1985) pp. 100–105 |
| [a9] | J. Riordan, "Combinatorial Identities" , Wiley (1968) |
How to Cite This Entry:
Lucas polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lucas_polynomials&oldid=17297
This article was adapted from an original article by Andreas N. Philippou (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article (cf. [a1] and [a5]) given by
(cf. [a1] and [a5]) given by

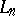 for
for 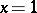 , and they satisfy several identities, which may be easily proved by induction, e.g.:
, and they satisfy several identities, which may be easily proved by induction, e.g.:





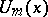 denote the Fibonacci polynomials;
denote the Fibonacci polynomials;

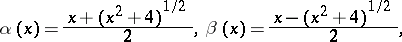
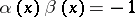 ; and
; and

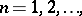
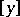 denotes the greatest integer in
denotes the greatest integer in 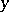 .
.
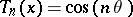 ,
, 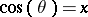 , by
, by

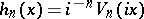 and the Lucas-type polynomials
and the Lucas-type polynomials


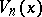 . These are
. These are 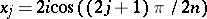 ,
, 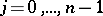 . Bicknell [a2] showed that
. Bicknell [a2] showed that 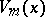 divides
divides  if and only if
if and only if  is an odd multiple of
is an odd multiple of 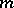 . G.E. Bergum and Hoggatt Jr. introduced in [a1] the bivariate Lucas polynomials
. G.E. Bergum and Hoggatt Jr. introduced in [a1] the bivariate Lucas polynomials 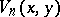 by the recursion
by the recursion

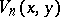 , and showed that the
, and showed that the 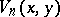 are irreducible polynomials over the rational numbers if and only if
are irreducible polynomials over the rational numbers if and only if 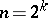 for some positive integer (cf. also Irreducible polynomial). The formula
for some positive integer (cf. also Irreducible polynomial). The formula

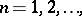
 or by expanding the generating function of
or by expanding the generating function of 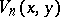 , generalizes (a8).
, generalizes (a8).
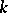 ,
, 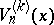 and
and 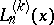 . The Lucas-type polynomials of order
. The Lucas-type polynomials of order 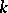 satisfy the recurrence
satisfy the recurrence


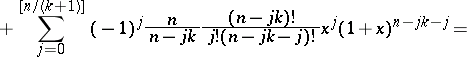
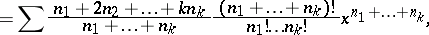
 such that
such that 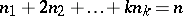 , and they are related to the Fibonacci-type polynomials of order
, and they are related to the Fibonacci-type polynomials of order 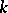 (cf. [a6] and [a8] and Fibonacci polynomials),
(cf. [a6] and [a8] and Fibonacci polynomials), 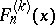 , by
, by


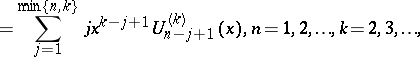
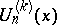 are the Fibonacci polynomials of order
are the Fibonacci polynomials of order 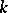 (cf. [a7]). Charalambides [a3] showed that the reliability of a circular consecutive
(cf. [a7]). Charalambides [a3] showed that the reliability of a circular consecutive 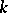 -out-of-
-out-of- :
:  -system,
-system, 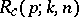 , whose components function independently with probability
, whose components function independently with probability 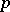 is given by
is given by

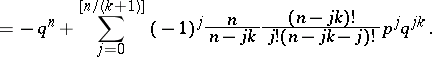
 and the length of the longest circular success run" Fibonacci Quart. , 29 (1991) pp. 290–297
and the length of the longest circular success run" Fibonacci Quart. , 29 (1991) pp. 290–297 , longest runs, and reliability of consecutive-
, longest runs, and reliability of consecutive- -out-of-
-out-of- :
: 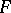 systems" A.N. Philippou (ed.) G.E. Bergum (ed.) A.F. Horadam (ed.) , Fibonacci Numbers and Their Applications , Reidel (1986) pp. 203–227
systems" A.N. Philippou (ed.) G.E. Bergum (ed.) A.F. Horadam (ed.) , Fibonacci Numbers and Their Applications , Reidel (1986) pp. 203–227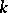 , multinomial expansions and probability" Internat. J. Math. Math. Sci. , 6 (1983) pp. 545–550
, multinomial expansions and probability" Internat. J. Math. Math. Sci. , 6 (1983) pp. 545–550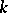 with probability applications" Fibonacci Quart. , 23 (1985) pp. 100–105
with probability applications" Fibonacci Quart. , 23 (1985) pp. 100–105