Isotropy representation

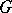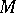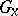The natural linear representation of the isotropy group of a differentiable transformation group in the tangent space to the underlying manifold. If is a group of differentiable transformations on a manifold and is the corresponding isotropy subgroup at the point 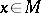, then the isotropy representation 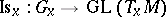associates with each 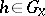the differential 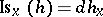of the transformation 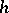at . The image of the isotropy representation, , is called the linear isotropy group at . If 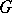is a Lie group with a countable base acting smoothly and transitively on 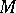, then the tangent space 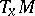can naturally be identified with the space 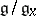, where 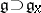are the Lie algebras of the groups 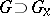. Furthermore, the isotropy representation 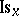is now identified with the representation induced by the restriction of the adjoint representation (cf. 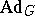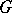Adjoint representation of a Lie group) of to .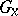

If a homogeneous space 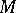is reductive, that is, if 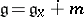, where 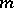is an invariant subspace with respect to 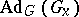, then 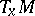can be identified with 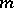, while 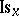can be identified with the representation 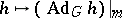(see [3]). In this case, the isotropy representation is faithful (cf. Faithful representation) if acts effectively.

The isotropy representation and linear isotropy group play an important role in the study of invariant objects on homogeneous spaces (cf. Invariant object). The invariant tensor fields on a homogeneous space 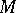are in one-to-one correspondence with the tensors on 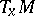that are invariant with respect to the isotropy representation. In particular, 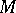has an invariant Riemannian metric if and only if 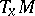has a Euclidean metric that is invariant under the linear isotropy group. There exists on the homogeneous space 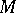a positive invariant measure if and only if 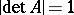for all 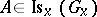. A homogeneous space has an invariant orientation if and only if 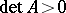for all 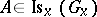. The invariant linear connections on 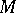are in one-to-one correspondence with the linear mappings 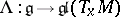with the following properties:

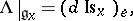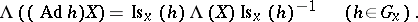A generalization of the concept of the isotropy representation is the concept of the isotropy representation of order . This is a homomorphism 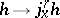of the group 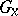into the group of invertible -jets of diffeomorphisms of the space 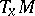taking the zero to itself. This concept is used in the study of invariant objects of higher orders.

References

[1]	R. Sulanke, P. Wintgen, "Differentialgeometrie und Faserbündel" , Deutsch. Verlag Wissenschaft. (1972)
[2]	S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978)
[3]	P.K. Rashevskii, "On the geometry of homogeneous spaces" , Proc. Sem. Vektor. Tenzor. Anal. i Prilozh. k Geom., Mekh. i Fiz. , 9 , Moscow-Leningrad (1952) pp. 49–74 (In Russian)
[4]	E. Cartan, "La théorie des groupes finis et continus et l'analyse situs" , Gauthier-Villars (1930)
[5]	S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 2 , Interscience (1969)

References

[a1]	S. Helgason, "Groups and geometric analysis" , Acad. Press (1984) pp. Chapt. II, Sect. 4