Zariski problem on field extensions

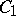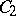The Zariski problem has its motivation in a geometric question. For example, one could ask the following: Given two curves and , make two surfaces by crossing a line with each curve. If the resulting surfaces are isomorphic, must the original curves also be isomorphic?

In general, one starts with two affine varieties, 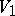and 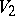, of dimension (cf. also Affine variety) and crosses each with a line. Associated to each 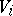is its coordinate ring 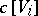, and from an algebraic point of view, one wants to know if the polynomial rings 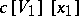and being isomorphic forces the coordinate rings to be isomorphic (cf. also Isomorphism). For larger than two, this is an open problem (as of 2000). However, also associated to each 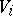is its function field, , and one wants to know if isomorphism of the rational function fields in one variable over the function fields forces the function fields to be isomorphic. This is the so-called Zariski problem.

The problem has an affirmative answer for varieties of dimension one. This result appears in [a3], but uses ideas from [a5] and in an essential way depends on Amitsur's results about function fields of genus zero [a1]. Using a wide range of ideas from algebraic geometry, [a2] provides a family of counterexamples to the problem. In particular, there exist a field and extension fields 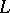of transcendence degree two over 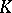that are not rational and yet is a pure transcendental extension of in five variables. Finally, in [a4] it is shown that the problem does have an affirmative answer most of the time, i.e., if the original varieties are of general type. Again, this result uses [a6] and, in an essential way, the results from [a7].

References

[a1]	S. Amitsur, "Generic splitting fields for central simple algebras" Ann. of Math. , 2 : 62 (1955) pp. 8–43
[a2]	A. Beauville, J.-L. Colliot-Thelene, J.-J. Sansuc, P. Swinnerton-Dyer, "Varietes stablement rationnelles non rationnelles" Ann. of Math. , 121 (1985) pp. 283–318
[a3]	J. Deveney, "Ruled function fields" Proc. Amer. Math. Soc. , 86 (1982) pp. 213–215
[a4]	J. Deveney, "The cancellation problem for function fields" Proc. Amer. Math. Soc. , 103 (1988) pp. 363–364
[a5]	M. Nagata, "A theorem on valuation rings and its applications" Nagoya Math. J. , 29 (1967) pp. 85–91
[a6]	J. Ohm, "The ruled residue theorem for simple transcendental extensions of valued fields" Proc. Amer. Math. Soc. , 89 (1983) pp. 16–18
[a7]	P. Roquette, "Isomorphisms of generic splitting fields of simple algebras" J. Reine Angew. Math. , 214/5 (1964) pp. 207–226