Difference between revisions of "Von Kármán vortex shedding"
Ulf Rehmann (talk | contribs) m (moved Von Kármán vortex shedding to Von Karman vortex shedding: ascii title) |
m (Automatically changed introduction) |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 93 formulas, 88 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|part}} | ||
''Kármán vortex shedding'' | ''Kármán vortex shedding'' | ||
A term defining the periodic detachment of pairs of alternate vortices from a bluff-body immersed in a fluid flow, generating an oscillating wake, or vortex street, behind it, and causing fluctuating forces to be experienced by the object. The phenomenon was first observed and analyzed on two-dimensional cylinders in a perpendicular uniform flow, but it is now widely documented for three-dimensional bodies and non-uniform flow fields. This is a situation where the energy subtracted from the flow field by the body drag is not dissipated directly into an irregular motion in the wake, but it is first transferred to a very regular vortex motion. The structure of the flow is then as schematically indicated in Fig.a1: | A term defining the periodic detachment of pairs of alternate vortices from a bluff-body immersed in a fluid flow, generating an oscillating wake, or vortex street, behind it, and causing fluctuating forces to be experienced by the object. The phenomenon was first observed and analyzed on two-dimensional cylinders in a perpendicular uniform flow, but it is now widely documented for three-dimensional bodies and non-uniform flow fields. This is a situation where the energy subtracted from the flow field by the body drag is not dissipated directly into an irregular motion in the wake, but it is first transferred to a very regular vortex motion. The structure of the flow is then as schematically indicated in Fig.a1: | ||
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/v130110a.gif" style="border:1px solid;"/> |
Figure: v130110a | Figure: v130110a | ||
| Line 11: | Line 19: | ||
The vortices at either side of the body have opposite intensities (directions of rotation) and are arranged in a particular geometrical pattern which can be observed even at some distance behind the obstacle. These vortices do not mix with the outer flow and are dissipated by viscosity only after a long time. It is this feature that allows a basic explanation of the phenomenon to be carried out in terms of inviscid flow, even if its origin can only be attributed to the viscosity, as will be discussed below. This idealized explanation was first proposed by Th. von Kármán [[#References|[a8]]], [[#References|[a9]]] (1911, 1912), and the phenomenon is since associated to his name, even if the first experimental observations were reported by the French physicist H. Bénard [[#References|[a10]]], [[#References|[a11]]], [[#References|[a13]]], [[#References|[a14]]], (1908, 1913, 1926) and A. Mallock [[#References|[a12]]] (1907); cf. also [[Ginzburg–Landau equation|Ginzburg–Landau equation]]. Early representations may be found in the drawings of Leonardo da Vinci and in Flemish paintings of the XVI century. | The vortices at either side of the body have opposite intensities (directions of rotation) and are arranged in a particular geometrical pattern which can be observed even at some distance behind the obstacle. These vortices do not mix with the outer flow and are dissipated by viscosity only after a long time. It is this feature that allows a basic explanation of the phenomenon to be carried out in terms of inviscid flow, even if its origin can only be attributed to the viscosity, as will be discussed below. This idealized explanation was first proposed by Th. von Kármán [[#References|[a8]]], [[#References|[a9]]] (1911, 1912), and the phenomenon is since associated to his name, even if the first experimental observations were reported by the French physicist H. Bénard [[#References|[a10]]], [[#References|[a11]]], [[#References|[a13]]], [[#References|[a14]]], (1908, 1913, 1926) and A. Mallock [[#References|[a12]]] (1907); cf. also [[Ginzburg–Landau equation|Ginzburg–Landau equation]]. Early representations may be found in the drawings of Leonardo da Vinci and in Flemish paintings of the XVI century. | ||
| − | Its idealized mathematical description, restricted to a two-dimensional flow, is based on the investigation of the stability of two parallel vortex sheets with vortices of equal but opposite intensity. Linear vortices of intensity | + | Its idealized mathematical description, restricted to a two-dimensional flow, is based on the investigation of the stability of two parallel vortex sheets with vortices of equal but opposite intensity. Linear vortices of intensity $\Gamma$ are located at equal distance from each other along these sheets and the motion resulting from the mutually induced velocity is investigated. (The intensity $\Gamma$ of a vortex is based on its circulation and is defined as $\Gamma : = \oint \overset{\rightharpoonup} { U } . d \overset{\rightharpoonup }{ r }$.) |
A quick investigation (discussed in detail below) shows that only two different vortex arrangements do not produce transversal induced velocities on each other: | A quick investigation (discussed in detail below) shows that only two different vortex arrangements do not produce transversal induced velocities on each other: | ||
| Line 17: | Line 25: | ||
a) one with the eddies of one row situated exactly opposite those of the other row; | a) one with the eddies of one row situated exactly opposite those of the other row; | ||
| − | b) the second with the opposite eddies symmetrically staggered, as in Fig.a1. However, a linear stability analysis with respect to small disturbances shows that the first configuration is always dynamically unstable, while the second one becomes stable for one geometrical configuration specified by a definite value of the ratio | + | b) the second with the opposite eddies symmetrically staggered, as in Fig.a1. However, a linear stability analysis with respect to small disturbances shows that the first configuration is always dynamically unstable, while the second one becomes stable for one geometrical configuration specified by a definite value of the ratio $b / l$ of the separation $b$ between the sheets, to the longitudinal vortex separation $l$. To be more accurate, at specific values of this ratio, the vortex pattern is in a situation of indifferent equilibrium with respect to disturbances of wave-length $2 l$, the important ones since they are responsible for the induced velocities between vortices. The result obtained by von Kármán for the above ratio is |
| − | + | \begin{equation*} \frac { b } { h } = \frac { 1 } { \pi } \operatorname { cosh } ^ { - 1 } \sqrt { 2 } \approx 0.2806, \end{equation*} | |
a value which is considered in very good agreement with the experimental observations for uniform flow around circular cylinders. Associated to this geometry there appears a particular longitudinal velocity for the ensemble of the alternating eddies, which was determined to be | a value which is considered in very good agreement with the experimental observations for uniform flow around circular cylinders. Associated to this geometry there appears a particular longitudinal velocity for the ensemble of the alternating eddies, which was determined to be | ||
| − | + | \begin{equation*} U_{\text{vortex}} = \frac { \Gamma } { l \sqrt { 8 } }, \end{equation*} | |
| − | that is, the vortices detach from the body at a lower speed than the external flow and trail behind it. This means that around each individual vortex there is a number of closed streamlines. It should be noted that the von Kármán approach does not give any hint on the values of | + | that is, the vortices detach from the body at a lower speed than the external flow and trail behind it. This means that around each individual vortex there is a number of closed streamlines. It should be noted that the von Kármán approach does not give any hint on the values of $b$ and $l$ relative to the dimension, or shape, of the body. This justifies the continuous actual research for the numerical solution to the problem, one of the challenging problems of present computational fluid dynamics (as of 2000). |
| − | This idealized formulation is based on the assumption of an inviscid fluid, while the generation of the vortices requires the fluid to be viscous. Also, as a consequence of the velocity defect of the vortex trail, the body shedding the vortices experiences a drag, leading to an apparent paradox. As stated by L. Prandtl [[#References|[a1]]], the explanation is given by the [[Boundary layer|boundary layer]] theory. From it, it can be seen that in the limit of viscosity equal to zero ( | + | This idealized formulation is based on the assumption of an inviscid fluid, while the generation of the vortices requires the fluid to be viscous. Also, as a consequence of the velocity defect of the vortex trail, the body shedding the vortices experiences a drag, leading to an apparent paradox. As stated by L. Prandtl [[#References|[a1]]], the explanation is given by the [[Boundary layer|boundary layer]] theory. From it, it can be seen that in the limit of viscosity equal to zero ($\mu = 0$), the fluid can be considered frictionless everywhere except in a thin layer close to the body, where a different limit process ($\mu \rightarrow 0$ and not $\mu = 0$) must be performed in the [[Navier–Stokes equations|Navier–Stokes equations]]. It is in this region, so small to be negligible in the context of the overall flow field, but in which friction forces cannot be neglected no matter how small the viscosity, that the vorticity found in the vortex sheet is created. |
==Induced velocities in vortex sheets.== | ==Induced velocities in vortex sheets.== | ||
| − | In inviscid fluid dynamics a vortex sheet can be defined as the ideal plane that separate two streams of uniform but different velocity. One assumes that all the vorticity associated with the velocity jump is concentrated on this plane. If the vorticity is carried by distinct vortices placed at equal intervals, then the individual intensity | + | In inviscid fluid dynamics a vortex sheet can be defined as the ideal plane that separate two streams of uniform but different velocity. One assumes that all the vorticity associated with the velocity jump is concentrated on this plane. If the vorticity is carried by distinct vortices placed at equal intervals, then the individual intensity $\Gamma$ is only a function of the velocity difference $\Delta U$ and separation $l$, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v130/v130110/v13011018.png"/>. Under these conditions it is easy to compute, for the two-dimensional case in a fluid at rest [[#References|[a2]]], the velocity induced on each vortex by all the others, and the eventual global displacement velocity of the sheets using the complex potential formulation of the velocity, where |
| − | + | \begin{equation*} \Phi = \phi - i \psi, \end{equation*} | |
with | with | ||
| − | + | \begin{equation*} w ( z ) = U _ { x } - i U _ { y } = \frac { d \Phi } { d z } , z = x + i y. \end{equation*} | |
| − | With this convention, a single vortex of intensity | + | With this convention, a single vortex of intensity $\Gamma$ located at $z_j$ has a complex potential |
| − | + | \begin{equation*} \Phi ( z ) = - \frac { i \Gamma } { 2 \pi } \operatorname { log } ( z - z _ { j } ). \end{equation*} | |
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/v130110b.gif" style="border:1px solid;"/> |
Figure: v130110b | Figure: v130110b | ||
| − | For an infinite single sheet of vortices with separation | + | For an infinite single sheet of vortices with separation $l$ and position $z = m l$, $m$ an integer, in a fluid at rest (cf. Fig.a2), the expression becomes |
| − | + | \begin{equation*} \Phi ( z ) = - \frac { i \Gamma } { 2 \pi } \sum _ { m = - \infty } ^ { \infty } \operatorname { log } ( z - ( z _ { 0 } - m l ) ), \end{equation*} | |
or | or | ||
| − | + | \begin{equation*} \Phi ( z ) = - \frac { i \Gamma } { 2 \pi } \operatorname { log } \left[ \prod _ { m = - \infty } ^ { \infty } ( z - ( z _ { 0 } - m l ) ) \right] = \end{equation*} | |
| − | + | \begin{equation*} = - \frac { i \Gamma } { 2 \pi } \operatorname { log } \left[ \operatorname { sin } \frac { \pi z } { l } \right] + \text{const}. \end{equation*} | |
| − | This corresponds to a velocity | + | This corresponds to a velocity $w ( m , l )$ of the vortices at $z = m l$: |
| − | + | \begin{equation*} w ( m , l ) = \frac { d \Phi } { d z } = - \frac { i \Gamma } { 2 \pi } \left[ \operatorname { cotan } \frac { \pi z } { l } - \frac { 1 } { z - m l } \right] \equiv 0. \end{equation*} | |
The velocity of each vortex is equal to zero and the single vortex row remains at rest. However [[#References|[a3]]], the sheet is not stable: Under even the slightest disturbance it becomes undulatory and experimental observation shows that it then curls up into a series of large vortices. | The velocity of each vortex is equal to zero and the single vortex row remains at rest. However [[#References|[a3]]], the sheet is not stable: Under even the slightest disturbance it becomes undulatory and experimental observation shows that it then curls up into a series of large vortices. | ||
| − | Consider now a double sheet of vortices [[#References|[a4]]] with distance | + | Consider now a double sheet of vortices [[#References|[a4]]] with distance $b$ between the sheets. All the vortices in each row have same intensity but the two rows have opposite senses of rotation. Even if the separation $l$ between the vortices is the same, many arrangements are possible, since those in opposite rows are not necessarily opposed to each other. Applying the same development as for the single sheet, it can be derived that only two different symmetrical vortex arrangements do not produce transversal induced velocities [[#References|[a5]]]: the first with the eddies of one row situated exactly opposite those of the other row, and the second with the opposite eddies symmetrically staggered. In these cases the velocities induced by one row on the other are such as to cause only a forward motion of the facing row. |
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/v130110c.gif" style="border:1px solid;"/> |
Figure: v130110c | Figure: v130110c | ||
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/v130110d.gif" style="border:1px solid;"/> |
Figure: v130110d | Figure: v130110d | ||
| − | For the case of vortices in opposition (Fig.a3) the induced velocity at vortex positions | + | For the case of vortices in opposition (Fig.a3) the induced velocity at vortex positions $z = m l + b / 2$, $z = m l - b / 2$ is |
| − | + | \begin{equation*} U = \frac { \Gamma } { 2 l } \operatorname { coth } \frac { \pi b } { l }, \end{equation*} | |
while for the alternating case (Fig.a4) one has | while for the alternating case (Fig.a4) one has | ||
| − | + | \begin{equation*} U = \frac { \Gamma } { 2 l } \operatorname { tanh } \frac { \pi b } { l }. \end{equation*} | |
In both cases, since the velocity is the same for each row, the result is a global displacement of the double vortex street. | In both cases, since the velocity is the same for each row, the result is a global displacement of the double vortex street. | ||
| Line 84: | Line 92: | ||
None of these arrangements is unconditionally stable under the effect of small perturbations, but it was the merit of von Kármán to show that, while the first is never stable, the alternate street may become so in certain particular geometrical vortex arrangements. For this case the complex potential is | None of these arrangements is unconditionally stable under the effect of small perturbations, but it was the merit of von Kármán to show that, while the first is never stable, the alternate street may become so in certain particular geometrical vortex arrangements. For this case the complex potential is | ||
| − | + | \begin{equation*} \Phi ( z ) = - \frac { i \Gamma } { 2 \pi } [ \operatorname { log } \operatorname { sin } \left( \frac { \pi } { l } \left( z - \frac { i b } { 2 } \right) \right) + \end{equation*} | |
| − | + | \begin{equation*} - \operatorname { log } \operatorname { sin } \left. \left( \frac { \pi } { l } \left( z - \frac { l } { 2 } + \frac { i b } { 2 } \right) \right) \right] + \text{const}. \end{equation*} | |
It is based on this formulation that the small perturbation analysis is carried out. Evaluation of the stream function from the relation above shows that around each individual vortex there is a number of closed stream lines. | It is based on this formulation that the small perturbation analysis is carried out. Evaluation of the stream function from the relation above shows that around each individual vortex there is a number of closed stream lines. | ||
==Stability analysis.== | ==Stability analysis.== | ||
| − | In the original analysis, vortices which are at a given time at position | + | In the original analysis, vortices which are at a given time at position $( m l + U t , \pm b / 2 )$ are assumed to be displaced to the position $( x _ { m, j} + m l + U t , y _ { m , j } \pm b / 2 )$ by a disturbance of the type |
| − | + | \begin{equation*} x _ { m , j } = \alpha _ { j } e ^ { i m \theta } , y _ { m , j } = \beta _ { j } e ^ { i m \theta } \end{equation*} | |
| − | + | \begin{equation*} [ z = \gamma _ { j } e ^ { i m \theta } , \gamma = \alpha + i \beta ] , 0 < \theta < \pi, \end{equation*} | |
| − | index | + | index $j$ indicating the upper or lower row. If $\theta$ is small, this has the character of an undulation of wave-length $2 \pi l / \theta$. |
| − | It is then possible to derive from the complex potential the equations for | + | It is then possible to derive from the complex potential the equations for $d \alpha_{ j } / d t$, $d \beta _ { j } / d t$ as functions of the various parameters. The solutions are of the type $e ^ { \lambda t }$, a positive $\lambda$ indicating instability. This is always the case for the symmetrical double row. For the non-symmetric case |
| − | + | \begin{equation*} \lambda = \frac { \Gamma } { 2 \pi l ^ { 2 } } ( B ^ { 2 } \mp \sqrt { A ^ { 2 } - C ^ { 2 } } ), \end{equation*} | |
| − | where | + | where $A$, $B$ and $C$ are long functions of $\theta$ and of the geometrical vortex arrangement. It suffices to say that for stability $A ^ { 2 } \leq C ^ { 2 }$ and that for $\theta = \pi$ (wave-length of disturbance equal to $2 l$), $C = 0$. So, for stability $A$ must vanish: |
| − | + | \begin{equation*} A = \frac { 1 } { 2 } \theta ( 2 \pi - \theta ) - \frac { \pi ^ { 2 } } { \operatorname { cosh } ^ { 2 } ( \pi b / l ) } = 0, \end{equation*} | |
or | or | ||
| − | + | \begin{equation*} \operatorname { cosh } ^ { 2 } \pi \frac { b } { l } = 2 ,\; \pi \frac { b } { l } \approx .8814 ,\; \frac { b } { l } \approx .2806, \end{equation*} | |
which is the result indicated in the introduction, and again | which is the result indicated in the introduction, and again | ||
| − | + | \begin{equation*} U = \frac { \Gamma } { 2 l } \operatorname { tanh } \frac { \pi b } { l } = \frac { \Gamma } { 2 l \sqrt { 2 } }. \end{equation*} | |
| − | In the original paper von Kármán stated, but did not prove, that stability exists for all values of | + | In the original paper von Kármán stated, but did not prove, that stability exists for all values of $\theta$ in the range $0$ to $2 \pi$, that is, for all possible disturbance wavelengths. The proof is given by H. Lamb [[#References|[a4]]], who proved it to hold true except for $\theta = 0$ or $\theta = 2 \pi$, a situation in which the period of the disturbance is infinite and all fluid particles will move as a whole. |
==Drag due to vortex shedding.== | ==Drag due to vortex shedding.== | ||
| − | As stated at the beginning, the drag of a body moving in a uniform flow can be computed using potential flow theory applied to the alternate shedding vortices. This result, also due to von Kármán for the case of a circular cylinder [[#References|[a6]]], is an apparent paradox, since inviscid fluids cannot produce drag, and is justified by the fact that the vorticity in the sheets is generated inside the body boundary layer, a region not taken in account in the above analysis. For a cylinder moving in a fluid at rest with velocity | + | As stated at the beginning, the drag of a body moving in a uniform flow can be computed using potential flow theory applied to the alternate shedding vortices. This result, also due to von Kármán for the case of a circular cylinder [[#References|[a6]]], is an apparent paradox, since inviscid fluids cannot produce drag, and is justified by the fact that the vorticity in the sheets is generated inside the body boundary layer, a region not taken in account in the above analysis. For a cylinder moving in a fluid at rest with velocity $V$, the vortex street moves with a velocity $V - U$. The motion in the wake of the cylinder is obviously unsteady, due to the periodic vortex shedding, but this difficulty is overcome by averaging over an observation time equal to the period between the release of two vortices of the same sheet: |
| − | + | \begin{equation*} T = \frac { l } { V - U }. \end{equation*} | |
| − | Over this time the transfer in momentum to the vortex sheet between a cross-section far upstream of the cylinder and a corresponding one far downstream is equal to | + | Over this time the transfer in momentum to the vortex sheet between a cross-section far upstream of the cylinder and a corresponding one far downstream is equal to $M _ { 1 } = \rho \Delta V l b = \rho \Gamma { b }$. Per unit time this becomes |
| − | + | \begin{equation*} d M _ { 1 } = \rho \frac { \Gamma { b } } { l } ( - U ), \end{equation*} | |
| − | where | + | where $b$ is the distance between the vortex sheets. Between the two reference sections, two other sources of resistance must be accounted for: that of the amount of fluid the velocity of which is reduced from that of the free flow, $V$, to that of the wake, $U$, and equal to [[#References|[a1]]] |
| − | + | \begin{equation*} d M _ { 2 } = \rho \frac { \Gamma b } { l } ( V - U ), \end{equation*} | |
and the momentum and pressure integral difference over the front and back sections, equal to | and the momentum and pressure integral difference over the front and back sections, equal to | ||
| − | + | \begin{equation*} d M _ { 3 } = \rho \frac { \Gamma ^ { 2 } } { 2 \pi l }. \end{equation*} | |
The total drag is then the sum | The total drag is then the sum | ||
| − | + | \begin{equation*} D = \rho \frac { \Gamma b } { l } ( V - 2 U ) + \rho \frac { \Gamma ^ { 2 } } { 2 \pi l } \approx \end{equation*} | |
| − | + | \begin{equation*} \approx \rho \frac { V ^ { 2 } } { l } \left[ 1.587 \frac { U } { V } - 0.628 ( \frac { U } { V } ) ^ { 2 } \right], \end{equation*} | |
if the values previously obtained for the stable sheet are used. | if the values previously obtained for the stable sheet are used. | ||
| − | Again, it should by noted that with the von Kármán theory it is not possible to calculate | + | Again, it should by noted that with the von Kármán theory it is not possible to calculate $l$, $b$ and $U$ for a given obstacle. However, it allows one to determine the drag when they are measured, for instance from a visualisation of the vortex trail and the frequency of vortex release. Experimental results are then in good agreement with the expected theoretical results. |
| − | Finally, denoting by | + | Finally, denoting by $\operatorname { Cd}$ the drag coefficient, defined as |
| − | + | \begin{equation*} \operatorname{Cd} = \frac { D } { \rho V ^ { 2 } b }, \end{equation*} | |
| − | and by | + | and by $f$ the frequency of the vortex release, then |
| − | + | \begin{equation*} \operatorname{Cd} \approx \frac { l } { b } , f \approx \frac { l } { U } , \operatorname{Cd} \approx \frac { f U } { d } , \operatorname{Cd} \approx \frac { 1 } { \operatorname{St} } , \end{equation*} | |
| − | where | + | where $\operatorname{St}$ is the [[Strouhal number|Strouhal number]], defined on the vortex street width and velocity. The fact that the drag coefficient and the Strouhal number are inversely proportional [[#References|[a7]]] for a wide range of two-dimensional bodies has been observed in a number of experiments. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> L. Prandtl, O.G. Tietjens, "Applied hydro and aeromechanics" , Dover (1957)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> E. Gyuon, J.P. Hulin, L. Petit, "Hydrodynamique physique" , Intereditions/Ed. du CNRS (1957)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> J.M. Robertson, "Hydrodynamics in theory and applications" , Prentice-Hall (1965)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> H. Lamb, "Hydrodynamics" , Cambridge Univ. Press (1932)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> A.W. Maue, "Zur Stabilität der Karmansche Wirbelstrasse" ''Z. Angew. Math. Mech.'' , '''20''' (1940) pp. 129–137</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> T. von Kármán, H.L. Rubach, "On the mechanisms of fluid resistance" ''Physik Z.'' , '''13''' (1912) pp. 49–59</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> S. Hoerner, "Fluid dynamic drag" S. Hoerner (ed.) (1962)</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> T. von Kármán, ''Nachr. Ges. Wissenschaft. Göttingen'' (1911) pp. 509–517</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> T. von Kármán, ''Nachr. Ges. Wissenschaft. Göttingen'' (1912) pp. 547–556</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> H. Bénard, ''C.R. Acad. Sci. Paris'' , '''147''' (1908) pp. 839–842; 970–972</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> H. Bénard, ''C.R. Acad. Sci. Paris'' , '''156''' (1913) pp. 1003–1005; 1225–1228</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> A. Mallock, ''Proc. Royal Soc.'' , '''A79''' (1907) pp. 262–265</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> H. Bénard, ''C.R. Acad. Sci. Paris'' , '''182''' (1926) pp. 1375–1377; 1523–1525</td></tr><tr><td valign="top">[a14]</td> <td valign="top"> H. Bénard, ''C.R. Acad. Sci. Paris'' , '''183''' (1926) pp. 20–22; 184–186; 379</td></tr></table> |
Latest revision as of 17:46, 1 July 2020
Kármán vortex shedding
A term defining the periodic detachment of pairs of alternate vortices from a bluff-body immersed in a fluid flow, generating an oscillating wake, or vortex street, behind it, and causing fluctuating forces to be experienced by the object. The phenomenon was first observed and analyzed on two-dimensional cylinders in a perpendicular uniform flow, but it is now widely documented for three-dimensional bodies and non-uniform flow fields. This is a situation where the energy subtracted from the flow field by the body drag is not dissipated directly into an irregular motion in the wake, but it is first transferred to a very regular vortex motion. The structure of the flow is then as schematically indicated in Fig.a1:
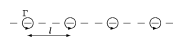
Figure: v130110a
The alternate vortex shedding is considered as responsible for a remarkable number of collapses of civil structures and damage to industrial equipment.
The vortices at either side of the body have opposite intensities (directions of rotation) and are arranged in a particular geometrical pattern which can be observed even at some distance behind the obstacle. These vortices do not mix with the outer flow and are dissipated by viscosity only after a long time. It is this feature that allows a basic explanation of the phenomenon to be carried out in terms of inviscid flow, even if its origin can only be attributed to the viscosity, as will be discussed below. This idealized explanation was first proposed by Th. von Kármán [a8], [a9] (1911, 1912), and the phenomenon is since associated to his name, even if the first experimental observations were reported by the French physicist H. Bénard [a10], [a11], [a13], [a14], (1908, 1913, 1926) and A. Mallock [a12] (1907); cf. also Ginzburg–Landau equation. Early representations may be found in the drawings of Leonardo da Vinci and in Flemish paintings of the XVI century.
Its idealized mathematical description, restricted to a two-dimensional flow, is based on the investigation of the stability of two parallel vortex sheets with vortices of equal but opposite intensity. Linear vortices of intensity $\Gamma$ are located at equal distance from each other along these sheets and the motion resulting from the mutually induced velocity is investigated. (The intensity $\Gamma$ of a vortex is based on its circulation and is defined as $\Gamma : = \oint \overset{\rightharpoonup} { U } . d \overset{\rightharpoonup }{ r }$.)
A quick investigation (discussed in detail below) shows that only two different vortex arrangements do not produce transversal induced velocities on each other:
a) one with the eddies of one row situated exactly opposite those of the other row;
b) the second with the opposite eddies symmetrically staggered, as in Fig.a1. However, a linear stability analysis with respect to small disturbances shows that the first configuration is always dynamically unstable, while the second one becomes stable for one geometrical configuration specified by a definite value of the ratio $b / l$ of the separation $b$ between the sheets, to the longitudinal vortex separation $l$. To be more accurate, at specific values of this ratio, the vortex pattern is in a situation of indifferent equilibrium with respect to disturbances of wave-length $2 l$, the important ones since they are responsible for the induced velocities between vortices. The result obtained by von Kármán for the above ratio is
\begin{equation*} \frac { b } { h } = \frac { 1 } { \pi } \operatorname { cosh } ^ { - 1 } \sqrt { 2 } \approx 0.2806, \end{equation*}
a value which is considered in very good agreement with the experimental observations for uniform flow around circular cylinders. Associated to this geometry there appears a particular longitudinal velocity for the ensemble of the alternating eddies, which was determined to be
\begin{equation*} U_{\text{vortex}} = \frac { \Gamma } { l \sqrt { 8 } }, \end{equation*}
that is, the vortices detach from the body at a lower speed than the external flow and trail behind it. This means that around each individual vortex there is a number of closed streamlines. It should be noted that the von Kármán approach does not give any hint on the values of $b$ and $l$ relative to the dimension, or shape, of the body. This justifies the continuous actual research for the numerical solution to the problem, one of the challenging problems of present computational fluid dynamics (as of 2000).
This idealized formulation is based on the assumption of an inviscid fluid, while the generation of the vortices requires the fluid to be viscous. Also, as a consequence of the velocity defect of the vortex trail, the body shedding the vortices experiences a drag, leading to an apparent paradox. As stated by L. Prandtl [a1], the explanation is given by the boundary layer theory. From it, it can be seen that in the limit of viscosity equal to zero ($\mu = 0$), the fluid can be considered frictionless everywhere except in a thin layer close to the body, where a different limit process ($\mu \rightarrow 0$ and not $\mu = 0$) must be performed in the Navier–Stokes equations. It is in this region, so small to be negligible in the context of the overall flow field, but in which friction forces cannot be neglected no matter how small the viscosity, that the vorticity found in the vortex sheet is created.
Induced velocities in vortex sheets.
In inviscid fluid dynamics a vortex sheet can be defined as the ideal plane that separate two streams of uniform but different velocity. One assumes that all the vorticity associated with the velocity jump is concentrated on this plane. If the vorticity is carried by distinct vortices placed at equal intervals, then the individual intensity $\Gamma$ is only a function of the velocity difference $\Delta U$ and separation $l$,  . Under these conditions it is easy to compute, for the two-dimensional case in a fluid at rest [a2], the velocity induced on each vortex by all the others, and the eventual global displacement velocity of the sheets using the complex potential formulation of the velocity, where
. Under these conditions it is easy to compute, for the two-dimensional case in a fluid at rest [a2], the velocity induced on each vortex by all the others, and the eventual global displacement velocity of the sheets using the complex potential formulation of the velocity, where
\begin{equation*} \Phi = \phi - i \psi, \end{equation*}
with
\begin{equation*} w ( z ) = U _ { x } - i U _ { y } = \frac { d \Phi } { d z } , z = x + i y. \end{equation*}
With this convention, a single vortex of intensity $\Gamma$ located at $z_j$ has a complex potential
\begin{equation*} \Phi ( z ) = - \frac { i \Gamma } { 2 \pi } \operatorname { log } ( z - z _ { j } ). \end{equation*}
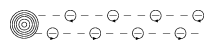
Figure: v130110b
For an infinite single sheet of vortices with separation $l$ and position $z = m l$, $m$ an integer, in a fluid at rest (cf. Fig.a2), the expression becomes
\begin{equation*} \Phi ( z ) = - \frac { i \Gamma } { 2 \pi } \sum _ { m = - \infty } ^ { \infty } \operatorname { log } ( z - ( z _ { 0 } - m l ) ), \end{equation*}
or
\begin{equation*} \Phi ( z ) = - \frac { i \Gamma } { 2 \pi } \operatorname { log } \left[ \prod _ { m = - \infty } ^ { \infty } ( z - ( z _ { 0 } - m l ) ) \right] = \end{equation*}
\begin{equation*} = - \frac { i \Gamma } { 2 \pi } \operatorname { log } \left[ \operatorname { sin } \frac { \pi z } { l } \right] + \text{const}. \end{equation*}
This corresponds to a velocity $w ( m , l )$ of the vortices at $z = m l$:
\begin{equation*} w ( m , l ) = \frac { d \Phi } { d z } = - \frac { i \Gamma } { 2 \pi } \left[ \operatorname { cotan } \frac { \pi z } { l } - \frac { 1 } { z - m l } \right] \equiv 0. \end{equation*}
The velocity of each vortex is equal to zero and the single vortex row remains at rest. However [a3], the sheet is not stable: Under even the slightest disturbance it becomes undulatory and experimental observation shows that it then curls up into a series of large vortices.
Consider now a double sheet of vortices [a4] with distance $b$ between the sheets. All the vortices in each row have same intensity but the two rows have opposite senses of rotation. Even if the separation $l$ between the vortices is the same, many arrangements are possible, since those in opposite rows are not necessarily opposed to each other. Applying the same development as for the single sheet, it can be derived that only two different symmetrical vortex arrangements do not produce transversal induced velocities [a5]: the first with the eddies of one row situated exactly opposite those of the other row, and the second with the opposite eddies symmetrically staggered. In these cases the velocities induced by one row on the other are such as to cause only a forward motion of the facing row.
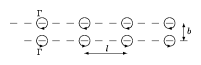
Figure: v130110c
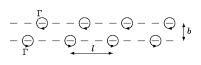
Figure: v130110d
For the case of vortices in opposition (Fig.a3) the induced velocity at vortex positions $z = m l + b / 2$, $z = m l - b / 2$ is
\begin{equation*} U = \frac { \Gamma } { 2 l } \operatorname { coth } \frac { \pi b } { l }, \end{equation*}
while for the alternating case (Fig.a4) one has
\begin{equation*} U = \frac { \Gamma } { 2 l } \operatorname { tanh } \frac { \pi b } { l }. \end{equation*}
In both cases, since the velocity is the same for each row, the result is a global displacement of the double vortex street.
None of these arrangements is unconditionally stable under the effect of small perturbations, but it was the merit of von Kármán to show that, while the first is never stable, the alternate street may become so in certain particular geometrical vortex arrangements. For this case the complex potential is
\begin{equation*} \Phi ( z ) = - \frac { i \Gamma } { 2 \pi } [ \operatorname { log } \operatorname { sin } \left( \frac { \pi } { l } \left( z - \frac { i b } { 2 } \right) \right) + \end{equation*}
\begin{equation*} - \operatorname { log } \operatorname { sin } \left. \left( \frac { \pi } { l } \left( z - \frac { l } { 2 } + \frac { i b } { 2 } \right) \right) \right] + \text{const}. \end{equation*}
It is based on this formulation that the small perturbation analysis is carried out. Evaluation of the stream function from the relation above shows that around each individual vortex there is a number of closed stream lines.
Stability analysis.
In the original analysis, vortices which are at a given time at position $( m l + U t , \pm b / 2 )$ are assumed to be displaced to the position $( x _ { m, j} + m l + U t , y _ { m , j } \pm b / 2 )$ by a disturbance of the type
\begin{equation*} x _ { m , j } = \alpha _ { j } e ^ { i m \theta } , y _ { m , j } = \beta _ { j } e ^ { i m \theta } \end{equation*}
\begin{equation*} [ z = \gamma _ { j } e ^ { i m \theta } , \gamma = \alpha + i \beta ] , 0 < \theta < \pi, \end{equation*}
index $j$ indicating the upper or lower row. If $\theta$ is small, this has the character of an undulation of wave-length $2 \pi l / \theta$.
It is then possible to derive from the complex potential the equations for $d \alpha_{ j } / d t$, $d \beta _ { j } / d t$ as functions of the various parameters. The solutions are of the type $e ^ { \lambda t }$, a positive $\lambda$ indicating instability. This is always the case for the symmetrical double row. For the non-symmetric case
\begin{equation*} \lambda = \frac { \Gamma } { 2 \pi l ^ { 2 } } ( B ^ { 2 } \mp \sqrt { A ^ { 2 } - C ^ { 2 } } ), \end{equation*}
where $A$, $B$ and $C$ are long functions of $\theta$ and of the geometrical vortex arrangement. It suffices to say that for stability $A ^ { 2 } \leq C ^ { 2 }$ and that for $\theta = \pi$ (wave-length of disturbance equal to $2 l$), $C = 0$. So, for stability $A$ must vanish:
\begin{equation*} A = \frac { 1 } { 2 } \theta ( 2 \pi - \theta ) - \frac { \pi ^ { 2 } } { \operatorname { cosh } ^ { 2 } ( \pi b / l ) } = 0, \end{equation*}
or
\begin{equation*} \operatorname { cosh } ^ { 2 } \pi \frac { b } { l } = 2 ,\; \pi \frac { b } { l } \approx .8814 ,\; \frac { b } { l } \approx .2806, \end{equation*}
which is the result indicated in the introduction, and again
\begin{equation*} U = \frac { \Gamma } { 2 l } \operatorname { tanh } \frac { \pi b } { l } = \frac { \Gamma } { 2 l \sqrt { 2 } }. \end{equation*}
In the original paper von Kármán stated, but did not prove, that stability exists for all values of $\theta$ in the range $0$ to $2 \pi$, that is, for all possible disturbance wavelengths. The proof is given by H. Lamb [a4], who proved it to hold true except for $\theta = 0$ or $\theta = 2 \pi$, a situation in which the period of the disturbance is infinite and all fluid particles will move as a whole.
Drag due to vortex shedding.
As stated at the beginning, the drag of a body moving in a uniform flow can be computed using potential flow theory applied to the alternate shedding vortices. This result, also due to von Kármán for the case of a circular cylinder [a6], is an apparent paradox, since inviscid fluids cannot produce drag, and is justified by the fact that the vorticity in the sheets is generated inside the body boundary layer, a region not taken in account in the above analysis. For a cylinder moving in a fluid at rest with velocity $V$, the vortex street moves with a velocity $V - U$. The motion in the wake of the cylinder is obviously unsteady, due to the periodic vortex shedding, but this difficulty is overcome by averaging over an observation time equal to the period between the release of two vortices of the same sheet:
\begin{equation*} T = \frac { l } { V - U }. \end{equation*}
Over this time the transfer in momentum to the vortex sheet between a cross-section far upstream of the cylinder and a corresponding one far downstream is equal to $M _ { 1 } = \rho \Delta V l b = \rho \Gamma { b }$. Per unit time this becomes
\begin{equation*} d M _ { 1 } = \rho \frac { \Gamma { b } } { l } ( - U ), \end{equation*}
where $b$ is the distance between the vortex sheets. Between the two reference sections, two other sources of resistance must be accounted for: that of the amount of fluid the velocity of which is reduced from that of the free flow, $V$, to that of the wake, $U$, and equal to [a1]
\begin{equation*} d M _ { 2 } = \rho \frac { \Gamma b } { l } ( V - U ), \end{equation*}
and the momentum and pressure integral difference over the front and back sections, equal to
\begin{equation*} d M _ { 3 } = \rho \frac { \Gamma ^ { 2 } } { 2 \pi l }. \end{equation*}
The total drag is then the sum
\begin{equation*} D = \rho \frac { \Gamma b } { l } ( V - 2 U ) + \rho \frac { \Gamma ^ { 2 } } { 2 \pi l } \approx \end{equation*}
\begin{equation*} \approx \rho \frac { V ^ { 2 } } { l } \left[ 1.587 \frac { U } { V } - 0.628 ( \frac { U } { V } ) ^ { 2 } \right], \end{equation*}
if the values previously obtained for the stable sheet are used.
Again, it should by noted that with the von Kármán theory it is not possible to calculate $l$, $b$ and $U$ for a given obstacle. However, it allows one to determine the drag when they are measured, for instance from a visualisation of the vortex trail and the frequency of vortex release. Experimental results are then in good agreement with the expected theoretical results.
Finally, denoting by $\operatorname { Cd}$ the drag coefficient, defined as
\begin{equation*} \operatorname{Cd} = \frac { D } { \rho V ^ { 2 } b }, \end{equation*}
and by $f$ the frequency of the vortex release, then
\begin{equation*} \operatorname{Cd} \approx \frac { l } { b } , f \approx \frac { l } { U } , \operatorname{Cd} \approx \frac { f U } { d } , \operatorname{Cd} \approx \frac { 1 } { \operatorname{St} } , \end{equation*}
where $\operatorname{St}$ is the Strouhal number, defined on the vortex street width and velocity. The fact that the drag coefficient and the Strouhal number are inversely proportional [a7] for a wide range of two-dimensional bodies has been observed in a number of experiments.
References
| [a1] | L. Prandtl, O.G. Tietjens, "Applied hydro and aeromechanics" , Dover (1957) |
| [a2] | E. Gyuon, J.P. Hulin, L. Petit, "Hydrodynamique physique" , Intereditions/Ed. du CNRS (1957) |
| [a3] | J.M. Robertson, "Hydrodynamics in theory and applications" , Prentice-Hall (1965) |
| [a4] | H. Lamb, "Hydrodynamics" , Cambridge Univ. Press (1932) |
| [a5] | A.W. Maue, "Zur Stabilität der Karmansche Wirbelstrasse" Z. Angew. Math. Mech. , 20 (1940) pp. 129–137 |
| [a6] | T. von Kármán, H.L. Rubach, "On the mechanisms of fluid resistance" Physik Z. , 13 (1912) pp. 49–59 |
| [a7] | S. Hoerner, "Fluid dynamic drag" S. Hoerner (ed.) (1962) |
| [a8] | T. von Kármán, Nachr. Ges. Wissenschaft. Göttingen (1911) pp. 509–517 |
| [a9] | T. von Kármán, Nachr. Ges. Wissenschaft. Göttingen (1912) pp. 547–556 |
| [a10] | H. Bénard, C.R. Acad. Sci. Paris , 147 (1908) pp. 839–842; 970–972 |
| [a11] | H. Bénard, C.R. Acad. Sci. Paris , 156 (1913) pp. 1003–1005; 1225–1228 |
| [a12] | A. Mallock, Proc. Royal Soc. , A79 (1907) pp. 262–265 |
| [a13] | H. Bénard, C.R. Acad. Sci. Paris , 182 (1926) pp. 1375–1377; 1523–1525 |
| [a14] | H. Bénard, C.R. Acad. Sci. Paris , 183 (1926) pp. 20–22; 184–186; 379 |
Von Kármán vortex shedding. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Von_K%C3%A1rm%C3%A1n_vortex_shedding&oldid=23117