Upper and lower limits
The upper (lower) limit of a sequence is the largest (respectively, smallest) limit among all partial (finite and infinite) limits of a given sequence of real numbers. For any sequence of real numbers 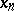 ,
, 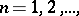 the set of all its partial limits (finite and infinite) on the extended number axis (i.e. in the set of real numbers, completed by the symbols
the set of all its partial limits (finite and infinite) on the extended number axis (i.e. in the set of real numbers, completed by the symbols 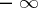 and
and 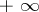 ) is non-empty and has both a largest and a smallest element (finite or infinite). The largest element of the set of partial limits is said to be the upper limit (lim sup) of the sequence and is denoted by
) is non-empty and has both a largest and a smallest element (finite or infinite). The largest element of the set of partial limits is said to be the upper limit (lim sup) of the sequence and is denoted by
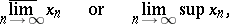 |
while the smallest element is said to be the lower limit (lim inf) and is denoted by
 |
For instance, if
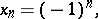 |
then
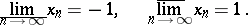 |
If
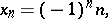 |
then
 |
If
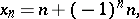 |
then
 |
Any sequence has a lim sup and a lim inf, and if the sequence is bounded from above (from below) its lim sup (lim inf) is finite. A number  is the lim sup (lim inf) of a sequence
is the lim sup (lim inf) of a sequence 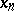 ,
, 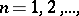 if and only if for any
if and only if for any 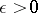 the following conditions are fulfilled: a) there exists a number
the following conditions are fulfilled: a) there exists a number 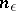 such that for all indices
such that for all indices 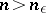 the inequality
the inequality  (
(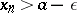 ) is true; b) for any index
) is true; b) for any index 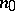 there exists an index
there exists an index 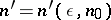 such that
such that 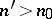 and
and 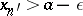 (
( ). The meaning of condition a) is that for a given
). The meaning of condition a) is that for a given  there exists in the sequence
there exists in the sequence  only a finite number of terms
only a finite number of terms 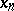 such that
such that 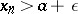 (
(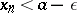 ). The meaning of condition b) is that there exists an infinite set of terms
). The meaning of condition b) is that there exists an infinite set of terms 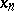 such that
such that 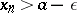 (
( ). Provided both are finite, the lim inf can be reduced to the lim sup by changing the signs of the terms of the sequence:
). Provided both are finite, the lim inf can be reduced to the lim sup by changing the signs of the terms of the sequence:
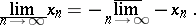 |
For a sequence  ,
,  to have a limit (finite or infinite (equal to one of the symbols
to have a limit (finite or infinite (equal to one of the symbols 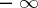 or
or 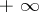 )) it is necessary and sufficient that
)) it is necessary and sufficient that
 |
The upper (lower) limit of a function 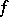 at a point
at a point 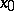 is the limit of the upper (lower) bounds of the sets of values of
is the limit of the upper (lower) bounds of the sets of values of 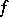 in a neighbourhood of
in a neighbourhood of  , when this neighbourhood contracts towards
, when this neighbourhood contracts towards 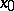 . These limits are denoted by
. These limits are denoted by
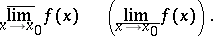 |
Let the function  be defined on a metric space
be defined on a metric space 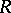 and assume real values. If
and assume real values. If 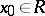 and
and 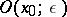 is an
is an  -neighbourhood of
-neighbourhood of  ,
, 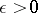 , then
, then
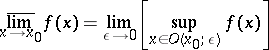 |
and
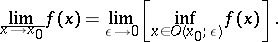 |
At each point  the function
the function  has both an upper limit
has both an upper limit 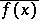 and a lower limit
and a lower limit 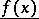 (finite or infinite). The function
(finite or infinite). The function 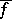 is upper semi-continuous, while the function
is upper semi-continuous, while the function 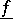 is lower semi-continuous on
is lower semi-continuous on 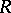 (in the sense of the concept of semi-continuity of functions which assume values in the extended number axis, cf. also Semi-continuous function).
(in the sense of the concept of semi-continuity of functions which assume values in the extended number axis, cf. also Semi-continuous function).
For a function 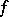 to have a finite or infinite (equal to
to have a finite or infinite (equal to  or
or 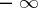 ) limit at a point
) limit at a point 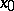 it is necessary and sufficient that
it is necessary and sufficient that
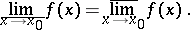 |
The concept of the upper limit (lower limit) of a function at a point can be naturally extended to real-valued functions defined on topological spaces.
The upper and lower limit of a sequence of sets 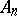 ,
, 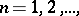 are the set
are the set
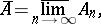 |
consisting of the elements  which belong to an infinite number of sets
which belong to an infinite number of sets 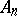 , and the set
, and the set
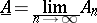 |
of the elements  which belong to all sets
which belong to all sets 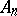 , starting from some index
, starting from some index 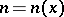 , respectively. Obviously,
, respectively. Obviously, 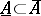 .
.
References
| [1] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian) |
| [2] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [3] | L.D. Kudryavtsev, "A course of mathematical analysis" , 1 , Moscow (1988) (In Russian) |
| [4] | S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian) |
| [5] | F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978)) |
Comments
The upper limit is also called the limes superior or limit superior, and the lower limit the limes inferior or limit inferior. Cf. also Upper and lower bounds.
The limit superior and limit inferior of a sequence of subsets 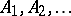 of a set are given by the formulas
of a set are given by the formulas
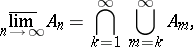 |
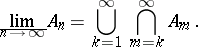 |
References
| [a1] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953) |
Upper and lower limits. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Upper_and_lower_limits&oldid=12152