Topological structure (topology)
open topology, respectively, closed topology
A collection  , respectively
, respectively  , of subsets of a set
, of subsets of a set  , satisfying the following properties: 1) The set
, satisfying the following properties: 1) The set  , as well as the empty set
, as well as the empty set  , are elements of the collection
, are elements of the collection  , respectively
, respectively  .
.
 , respectively
, respectively  . The intersection, respectively union, of a finite number, and the union, respectively intersection, of any number of elements of
. The intersection, respectively union, of a finite number, and the union, respectively intersection, of any number of elements of 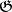 , respectively
, respectively  , is an element of the same collection.
, is an element of the same collection.
Once a topology, or topological structure, has been introduced or defined on a set  , the set is called a topological space, its elements are called points and the elements of the collection
, the set is called a topological space, its elements are called points and the elements of the collection 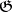 , respectively
, respectively  , are called the open, respectively closed, sets of this topological space.
, are called the open, respectively closed, sets of this topological space.
If one of the collections  or
or  of subsets of
of subsets of  is defined, satisfying property 1 and
is defined, satisfying property 1 and  or
or 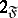 , respectively, then the other collection may be defined by duality as consisting of the complements of the elements of the first collection.
, respectively, then the other collection may be defined by duality as consisting of the complements of the elements of the first collection.
Comments
See also Topology, general; Topological space; General topology.
References
| [a1] | R. Engelking, "General topology" , Heldermann (1989) |
Topological structure (topology). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Topological_structure_(topology)&oldid=18647