Sullivan minimal model
The theory of minimal models began with the work of D. Quillen [a5]. A simply-connected topological space 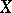 (cf. also Simply-connected domain) is called rational if its homotopy groups are rational vector spaces (cf. also Homotopy group; Vector space). The rationalization functor associates to each simply-connected space
(cf. also Simply-connected domain) is called rational if its homotopy groups are rational vector spaces (cf. also Homotopy group; Vector space). The rationalization functor associates to each simply-connected space 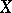 a mapping
a mapping 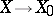 , such that
, such that 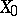 is rational and
is rational and 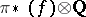 is an isomorphism. The interest of this construction is that the homotopy category of rational spaces has an algebraic nature. More precisely, in [a5], D. Quillen established an equivalence of homotopy categories between the homotopy category of simply-connected rational spaces and the homotopy category of connected differential graded Lie algebras (cf. also Lie algebra, graded).
is an isomorphism. The interest of this construction is that the homotopy category of rational spaces has an algebraic nature. More precisely, in [a5], D. Quillen established an equivalence of homotopy categories between the homotopy category of simply-connected rational spaces and the homotopy category of connected differential graded Lie algebras (cf. also Lie algebra, graded).
In [a6], D. Sullivan associated to each space 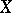 a commutative differential graded algebra (CDGA),
a commutative differential graded algebra (CDGA),  , which is linked to the cochain algebra
, which is linked to the cochain algebra 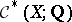 by a chain of differential graded algebra quasi-isomorphisms (i.e. morphisms inducing isomorphisms in cohomology). This, in particular, gave a solution to Thom's problem of constructing commutative cochains over the rationals. The
by a chain of differential graded algebra quasi-isomorphisms (i.e. morphisms inducing isomorphisms in cohomology). This, in particular, gave a solution to Thom's problem of constructing commutative cochains over the rationals. The 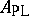 -functor together with its adjoint, the realization functor of a commutative differential graded algebra, induce an equivalence of homotopy categories between the homotopy category of simply-connected rational spaces with finite Betti numbers and the homotopy category of rational commutative differential graded algebras,
-functor together with its adjoint, the realization functor of a commutative differential graded algebra, induce an equivalence of homotopy categories between the homotopy category of simply-connected rational spaces with finite Betti numbers and the homotopy category of rational commutative differential graded algebras, 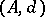 , such that
, such that 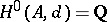 ,
, 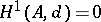 , and
, and 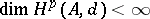 for each
for each 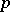 .
.
The correspondence
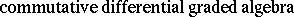 |
 |
 |
behaves well with respect to fibrations and cofibrations (cf. also Fibration). Rational homotopy invariants of a space are most easily obtained by means of constructions in the category of commutative differential graded algebras. This procedure has been made very powerful with the Sullivan minimal models.
Let 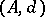 be a commutative differential graded algebra such that
be a commutative differential graded algebra such that 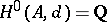 ,
,  , and
, and 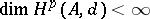 for each
for each 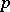 . There exists then a quasi-isomorphism of commutative differential graded algebras
. There exists then a quasi-isomorphism of commutative differential graded algebras 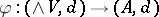 , where
, where 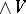 denotes the free commutative algebra on the graded vector space of finite type
denotes the free commutative algebra on the graded vector space of finite type  , and
, and 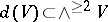 . The cochain algebra
. The cochain algebra 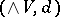 is called the Sullivan minimal model of
is called the Sullivan minimal model of 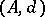 ; it is unique up to isomorphism.
; it is unique up to isomorphism.
The Sullivan minimal model of 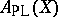 is called the Sullivan minimal model of
is called the Sullivan minimal model of 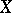 . It satisfies
. It satisfies 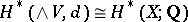 and
and 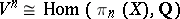 . More generally, for each continuous mapping
. More generally, for each continuous mapping 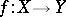 , there is a commutative diagram
, there is a commutative diagram
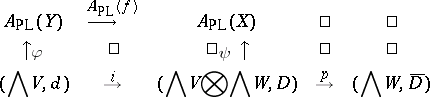 |
where 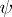 and
and 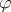 are quasi-isomorphisms,
are quasi-isomorphisms, 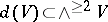 ,
, 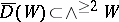 , and where
, and where 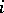 and
and 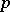 are the canonical injection and projection. In this case, the Grivel–Halperin–Thomas theorem asserts that
are the canonical injection and projection. In this case, the Grivel–Halperin–Thomas theorem asserts that 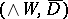 is a Sullivan minimal model for the homotopy fibre of
is a Sullivan minimal model for the homotopy fibre of 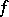 [a4].
[a4].
A key result in the theory is the so-called mapping theorem [a1]. Recall that the Lyusternik–Shnirel'man category of 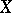 is the least integer
is the least integer  such that
such that 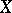 can be covered by
can be covered by 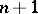 open sets each contractible in
open sets each contractible in 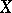 (cf. also Category (in the sense of Lyusternik–Shnirel'man)). If
(cf. also Category (in the sense of Lyusternik–Shnirel'man)). If 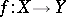 is a mapping between simply-connected spaces and if
is a mapping between simply-connected spaces and if 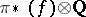 is injective, then
is injective, then 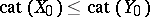 . The Lyusternik–Shnirel'man category of
. The Lyusternik–Shnirel'man category of 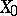 can be computed directly from its Sullivan minimal model
can be computed directly from its Sullivan minimal model 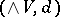 . Indeed, consider the following commutative diagram:
. Indeed, consider the following commutative diagram:
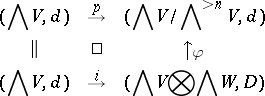 |
where 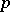 and
and  denote the canonical projection and injection and
denote the canonical projection and injection and 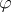 is a quasi-isomorphism. The category of
is a quasi-isomorphism. The category of 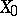 is then the least integer
is then the least integer  such that
such that 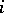 admits a retraction [a1].
admits a retraction [a1].
To obtain properties of simply-connected spaces with finite category, it is therefore sufficient to consider Sullivan minimal models 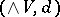 with finite category. Using this procedure, Y. Félix, S. Halperin and J.-C. Thomas have obtained the following dichotomy theorem: Either
with finite category. Using this procedure, Y. Félix, S. Halperin and J.-C. Thomas have obtained the following dichotomy theorem: Either 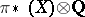 is finite-dimensional (the space is called elliptic), or else the sequence
is finite-dimensional (the space is called elliptic), or else the sequence 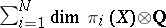 has exponential growth (the space is thus called hyperbolic) [a2].
has exponential growth (the space is thus called hyperbolic) [a2].
When 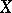 is elliptic, the dimension of
is elliptic, the dimension of 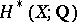 is finite, the Euler characteristic is non-negative and the rational cohomology algebra satisfies Poincaré duality [a3].
is finite, the Euler characteristic is non-negative and the rational cohomology algebra satisfies Poincaré duality [a3].
The minimal model of  contains all the rational homotopy invariants of
contains all the rational homotopy invariants of 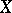 . For instance, the cochain algebra
. For instance, the cochain algebra 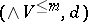 is a model for the
is a model for the 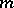 th Postnikov tower
th Postnikov tower 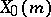 of
of 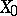 (cf. also Postnikov system), and the mapping
(cf. also Postnikov system), and the mapping 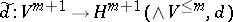 induced by
induced by 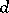 is the dual of the
is the dual of the 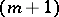 st
st  -invariant
-invariant
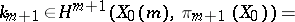 |
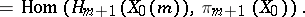 |
The quadratic part of the differential 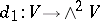 is dual to the Whitehead product in
is dual to the Whitehead product in 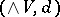 . More precisely,
. More precisely, 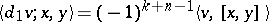 ,
, 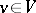 ,
, 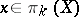 ,
, 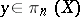 .
.
References
| [a1] | Y. Félix, S. Halperin, "Rational LS category and its applications" Trans. Amer. Math. Soc. , 273 (1982) pp. 1–37 |
| [a2] | Y. Félix, S. Halperin, J.C. Thomas, "Rational homotopy theory" (in preparation) |
| [a3] | S. Halperin, "Finiteness in the minimal models of Sullivan" Trans. Amer. Math. Soc. , 230 (1977) pp. 173–199 |
| [a4] | S. Halperin, "Lectures on minimal models" Mémoire de la SMF , 9/10 (1983) |
| [a5] | D. Quillen, "Rational homotopy theory" Ann. of Math. , 90 (1969) pp. 205–295 |
| [a6] | D. Sullivan, "Infinitesimal computations in topology" Publ. IHES , 47 (1977) pp. 269–331 |
Sullivan minimal model. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sullivan_minimal_model&oldid=11595