Subgroup
A non-empty subset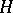 
of a group 
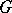which itself is a group with respect to the operation defined on 
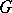. A subset 
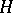of a group 
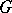is a subgroup of 
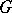if and only if: 1) 
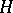contains the product of any two elements from 
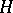; and 2) 
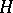contains together with any element 
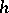the inverse 
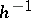. In the cases of finite and periodic groups, condition 2) is superfluous.
The subset of a group G consisting of the element 1 only is clearly a subgroup; it is called the unit subgroup of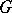 
and is usually denoted by 
. Also, 
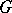itself is a subgroup. A subgroup different from 
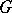is called a proper subgroup of 
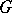. A proper subgroup of an infinite group can be isomorphic to the group itself. The group 
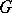itself and the subgroup 
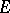are called improper subgroups of 
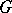, while all the others are called proper ones.
The set-theoretic intersection of any two (or any set of) subgroups of a group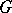 
is a subgroup of 
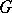. The intersection of all subgroups of 
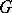containing all elements of a certain non-empty set 
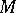is called the subgroup generated by the set 
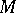and is denoted by 
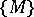. If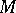 
consists of one element 
, then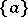 
is called the cyclic subgroup of the element 
. A group that coincides with one of its cyclic subgroups is called a cyclic group.
A set-theoretic union of subgroups is, in general, not a subgroup. By the join of subgroups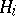 
, 
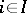, one means the subgroup generated by the union of the sets 
.
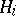The product of two subsets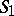 
and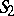 
of a group 
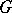is the set consisting of all possible (different) products 
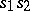, where 
, 
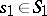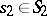. The product of two subgroups 
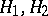is a subgroup if and only if 
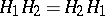, and in that case the product 
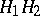coincides with the subgroup generated by 
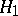and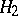 
(i.e. with the join of 
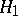and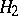 
).
A homomorphic image of a subgroup is a subgroup. If a group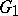 
is isomorphic to a subgroup 
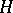of a group 
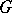, one says that 
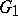can be imbedded in 
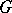(as groups). If one is given two groups and each of them is isomorphic to a proper subgroup of the other, it does not necessarily follow that these groups themselves are isomorphic (cf. also Homomorphism; Isomorphism).
Comments
References
| [a1] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) |
| [a2] | M. Hall jr., "The theory of groups" , Macmillan (1959) pp. 124 |
Subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Subgroup&oldid=12801