Difference between revisions of "Steiner curve"
From Encyclopedia of Mathematics
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| − | A plane algebraic curve of order four, described by the point on a circle of radius | + | {{TEX|done}} |
| + | A plane algebraic curve of order four, described by the point on a circle of radius $r$ rolling upon a circle of radius $R=3r$ and having with it internal tangency; a [[Hypocycloid|hypocycloid]] with modulus $m=3$. A Steiner curve is expressed by the following equation in rectangular Cartesian coordinates: | ||
| − | + | $$(x^2+y^2)^2+8rx(3y^2-x^2)+18r^2(x^2+y^2)-27r^4=0.$$ | |
A Steiner curve has three cusps (see Fig. a). | A Steiner curve has three cusps (see Fig. a). | ||
| Line 9: | Line 10: | ||
Figure: s087650a | Figure: s087650a | ||
| − | The length of the arc from the point | + | The length of the arc from the point $A$ is: |
| − | + | $$l=\frac{16}{3}r\sin^2\frac t4.$$ | |
| − | The length of the entire curve is | + | The length of the entire curve is $16r$. The radius of curvature is $r_k=8\sin(t/2)$. The area bounded by the curve is $S=2\pi r^2$. |
This curve was studied by Jacob Steiner (1798–1863). | This curve was studied by Jacob Steiner (1798–1863). | ||
Revision as of 21:04, 11 April 2014
A plane algebraic curve of order four, described by the point on a circle of radius $r$ rolling upon a circle of radius $R=3r$ and having with it internal tangency; a hypocycloid with modulus $m=3$. A Steiner curve is expressed by the following equation in rectangular Cartesian coordinates:
$$(x^2+y^2)^2+8rx(3y^2-x^2)+18r^2(x^2+y^2)-27r^4=0.$$
A Steiner curve has three cusps (see Fig. a).
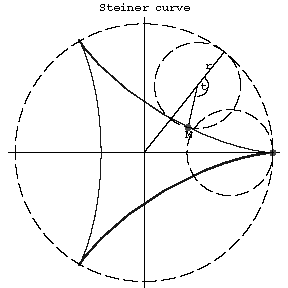
Figure: s087650a
The length of the arc from the point $A$ is:
$$l=\frac{16}{3}r\sin^2\frac t4.$$
The length of the entire curve is $16r$. The radius of curvature is $r_k=8\sin(t/2)$. The area bounded by the curve is $S=2\pi r^2$.
This curve was studied by Jacob Steiner (1798–1863).
References
| [1] | J. Steiner, "Werke" , 1–2 , Springer (1880–1882) |
Comments
References
| [a1] | M. Berger, "Geometry" , 1–2 , Springer (1987) pp. §9.14.34 (Translated from French) |
| [a2] | F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971) |
How to Cite This Entry:
Steiner curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Steiner_curve&oldid=17466
Steiner curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Steiner_curve&oldid=17466
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article