Spinor group

of a non-generate quadratic form 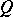on an -dimensional vector space 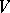(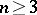) over a field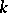

A connected linear algebraic group which is the simply-connected covering of the irreducible component 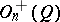of the identity of the orthogonal group 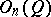of the form 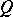. If 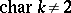, then 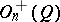coincides with the special orthogonal group 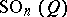. The spinor group is constructed in the following way. Let 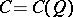be the Clifford algebra of the pair 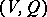, let 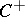(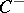) be the subspace of 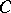generated by products of an even (odd) number of elements of 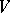, and let 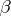be the canonical anti-automorphism of 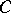defined by the formula

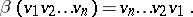The inclusion 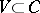enables one to define the Clifford group

and the even (or special) Clifford group

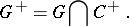The spinor group 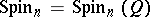is defined by

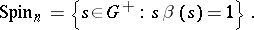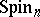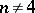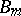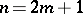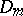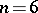The spinor group is a quasi-simple (when ), connected, simply-connected, linear algebraic group, of type when and of type when ; if it is 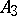and if 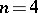it is 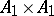. The following isomorphisms hold:

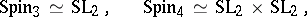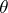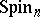There is a linear representation of in 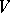defined by

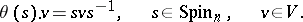If ,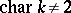

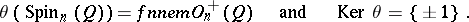The group 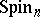has a faithful linear representation in 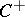(see Spinor representation).

If 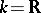is the field of real numbers and 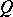is positive (or negative) definite, then the group 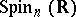of real points of the algebraic group 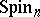is sometimes also called a spinor group. This is a connected simply-connected compact Lie group which is a two-sheeted covering of the special orthogonal group 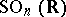. The following isomorphisms hold:

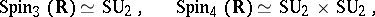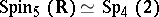(see Symplectic group),

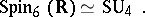References

[1]	H. Weyl, "The classical groups, their invariants and representations" , Princeton Univ. Press (1946)
[2]	J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955)
[3]	E. Cartan, "Leçons sur la théorie des spineurs" , 2 , Hermann (1938)
[4]	M.M. Postnikov, "Lie groups and Lie algebras" , Moscow (1982) (In Russian)
[5]	C. Chevalley, "Theory of Lie groups" , 1 , Princeton Univ. Press (1946)

Comments

See also Quadratic form.

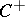is the so-called even Clifford algebra of .

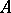References

[a1]	N. Bourbaki, "Algèbre. Formes sesquilineares et formes quadratiques" , Eléments de mathématiques , Hermann (1959) pp. Chapt. 9
[a2]	C. Chevalley, "The algebraic theory of spinors" , Columbia Univ. Press (1954)
[a3]	Th. Bröcker, T. Tom Dieck, "Representations of compact Lie groups" , Springer (1985)