Difference between revisions of "Skew-symmetric matrix"
(Importing text file) |
(TeX partially done) |
||
| Line 1: | Line 1: | ||
| − | A square [[ | + | A square [[matrix]] $A$ over a field of characteristic $\ne 2$ such that $A^T = -A$. The rank of a skew-symmetric matrix is an even number. Any square matrix $B$ over a field of characteristic $=ne 2$ is the sum of a [[symmetric matrix]] and a skew-symmetric matrix: |
| − | + | $$ | |
| − | + | B = \frac12(B + B^T) + \frac12(B - B^T) \ . | |
| − | + | $$ | |
| − | The non-zero roots of the characteristic polynomial of a real skew-symmetric matrix are purely imaginary | + | The non-zero roots of the [[characteristic polynomial]] of a real skew-symmetric matrix are purely [[imaginary number]]s. A real skew-symmetric matrix is [[Similar matrices|similar]] to a matrix |
| − | + | $$ | |
| − | + | \text{diag}[A_1,A_2,\ldots,A_t,0,0,\ldots] | |
| − | + | $$ | |
where | where | ||
| + | $$ | ||
| + | A_i = \alpha_i \left({ \begin{array}{cc}{ 0 & 1 \\ -1 & 0 }\end{array} }\right) | ||
| + | $$ | ||
| + | with $\alpha_i$ real numbers, $i = 1,\ldots,t$. The [[Jordan normal form]] $J$ of a complex skew-symmetric matrix possesses the following properties: 1) a Jordan cell $J_m(\lambda)$ with elementary divisor $(X-\lambda)^m$, where $\lambda \ne 0$, is repeated in $J$ as many times as is the cell $J_m(-\lambda)$; and 2) if $m$ is even, the Jordan cell $J_m(0)$ with elementary divisor $X^m$ is repeated in $J$ an even number of times. Any complex Jordan matrix with the properties 1) and 2) is similar to some skew-symmetric matrix. | ||
| − | + | The set of all skew-symmetric matrices of order $n$ over a field $k$ forms a [[Lie algebra]] over $k$ with respect to matrix addition and the commutator $[A,B] = AB - BA$. | |
| − | |||
| − | |||
| − | |||
| − | The set of all skew-symmetric matrices of order | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , '''1''' , Chelsea, reprint (1977) (Translated from Russian)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , '''1''' , Chelsea, reprint (1977) (Translated from Russian)</TD></TR> | ||
| + | </table> | ||
| Line 24: | Line 26: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) pp. Chapt. X</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) pp. Chapt. X</TD></TR> | ||
| + | </table> | ||
| + | |||
| + | {{TEX|part}} | ||
Revision as of 20:18, 7 April 2016
A square matrix $A$ over a field of characteristic $\ne 2$ such that $A^T = -A$. The rank of a skew-symmetric matrix is an even number. Any square matrix $B$ over a field of characteristic $=ne 2$ is the sum of a symmetric matrix and a skew-symmetric matrix: $$ B = \frac12(B + B^T) + \frac12(B - B^T) \ . $$ The non-zero roots of the characteristic polynomial of a real skew-symmetric matrix are purely imaginary numbers. A real skew-symmetric matrix is similar to a matrix $$ \text{diag}[A_1,A_2,\ldots,A_t,0,0,\ldots] $$ where $$ A_i = \alpha_i \left({ \begin{array}{cc}{ 0 & 1 \\ -1 & 0 }\end{array} }\right) $$ with $\alpha_i$ real numbers, $i = 1,\ldots,t$. The Jordan normal form $J$ of a complex skew-symmetric matrix possesses the following properties: 1) a Jordan cell $J_m(\lambda)$ with elementary divisor $(X-\lambda)^m$, where $\lambda \ne 0$, is repeated in $J$ as many times as is the cell $J_m(-\lambda)$; and 2) if $m$ is even, the Jordan cell $J_m(0)$ with elementary divisor $X^m$ is repeated in $J$ an even number of times. Any complex Jordan matrix with the properties 1) and 2) is similar to some skew-symmetric matrix.
The set of all skew-symmetric matrices of order $n$ over a field $k$ forms a Lie algebra over $k$ with respect to matrix addition and the commutator $[A,B] = AB - BA$.
References
| [1] | F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1977) (Translated from Russian) |
Comments
The Lie algebra of skew-symmetric matrices over a field 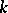 of size
of size  is denoted by
is denoted by 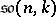 . The complex Lie algebras
. The complex Lie algebras  (
(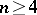 ) and
) and 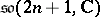 (
(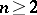 ) are simple of type
) are simple of type 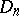 and
and 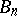 , respectively.
, respectively.
References
| [a1] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) pp. Chapt. X |
Skew-symmetric matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Skew-symmetric_matrix&oldid=14074