|
|
| Line 1: |
Line 1: |
| | + | {{TEX|done}} |
| | One of the [[Trigonometric functions|trigonometric functions]]: | | One of the [[Trigonometric functions|trigonometric functions]]: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s0854801.png" /></td> </tr></table>
| + | $$y=\sin x.$$ |
| | | | |
| − | The domain of definition is the whole real line and the range of values is the interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s0854802.png" />. The sine is an odd periodic function of period <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s0854803.png" />. Sine and [[Cosine|cosine]] are connected by the formula | + | The domain of definition is the whole real line and the range of values is the interval $[-1,1]$. The sine is an odd periodic function of period $2\pi$. Sine and [[Cosine|cosine]] are connected by the formula |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s0854804.png" /></td> </tr></table>
| + | $$\sin^2x+\cos^2x=1.$$ |
| | | | |
| | Sine and [[Cosecant|cosecant]] are connected by the formula | | Sine and [[Cosecant|cosecant]] are connected by the formula |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s0854805.png" /></td> </tr></table>
| + | $$\sin x=\frac{1}{\operatorname{cosec}x}.$$ |
| | | | |
| | The derivative of sine is: | | The derivative of sine is: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s0854806.png" /></td> </tr></table>
| + | $$(\sin x)'=\cos x.$$ |
| | | | |
| | The indefinite integral of sine is: | | The indefinite integral of sine is: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s0854807.png" /></td> </tr></table>
| + | $$\int\sin xdx=-\cos x+C.$$ |
| | | | |
| | Sine has the following power series representation: | | Sine has the following power series representation: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s0854808.png" /></td> </tr></table>
| + | $$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\ldots,\quad-\infty<x<\infty.$$ |
| | | | |
| | The function inverse to sine is called arcsine. | | The function inverse to sine is called arcsine. |
| | | | |
| − | The sine and cosine of a complex argument <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s0854809.png" /> are related to the exponential function by Euler's formulas: | + | The sine and cosine of a complex argument $z$ are related to the exponential function by Euler's formulas: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548010.png" /></td> </tr></table>
| + | $$e^{iz}=\cos z+i\sin z,\\\sin z=\frac{e^{iz}-e^{-iz}}{2i},$$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548011.png" /></td> </tr></table>
| + | and if $z=ix$ is pure imaginary, then |
| | | | |
| − | and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548012.png" /> is pure imaginary, then
| + | $$\sin ix=-\sinh x,$$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548013.png" /></td> </tr></table>
| + | where $\sinh x$ is the hyperbolic sine. |
| − | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548014.png" /> is the hyperbolic sine. | |
| | | | |
| | | | |
| | | | |
| | ====Comments==== | | ====Comments==== |
| − | Of course, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548015.png" /> can be defined by the Euler formulas or by its power series. A visual definition runs as follows. Consider the unit circle with centre at the origin <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548016.png" /> in a rectangular coordinate system and with a rotating radius vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548017.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548018.png" /> be the angle between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548019.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548020.png" /> (being reckoned positive in the counter-clockwise direction) and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548021.png" /> be the projection of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548022.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548023.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548024.png" /> is defined as the ratio <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548025.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548026.png" /> as the ratio <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548027.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548028.png" /> as the ratio <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548029.png" />. | + | Of course, $\sin x$ can be defined by the Euler formulas or by its power series. A visual definition runs as follows. Consider the unit circle with centre at the origin $O$ in a rectangular coordinate system and with a rotating radius vector $OP$. Let $x$ be the angle between $OA$ and $OP$ (being reckoned positive in the counter-clockwise direction) and let $P'$ be the projection of $P$ on $OA$. Then $\sin x$ is defined as the ratio $(PP')/(OP)$, $\cos x$ as the ratio $(OP')/(OP)$ and $\tan x$ as the ratio $(PP')/(OP')$. |
| | | | |
| | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s085480a.gif" /> | | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s085480a.gif" /> |
| Line 46: |
Line 45: |
| | Figure: s085480a | | Figure: s085480a |
| | | | |
| − | Another, analytical, approach starts with the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548030.png" /> defined on the closed interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548031.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548032.png" />. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548033.png" /> this integral is improper, but convergent. It is easy to see that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548034.png" /> is monotone increasing and continuous on the closed interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548035.png" /> and differentiable on the open interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548036.png" />, and has values in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548037.png" />. So it has an inverse function, defined on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548038.png" />, with values in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548039.png" />. This function is called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548040.png" />, and it can be proved that the domain of definition of this function can be continued to the whole real axis. The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548041.png" /> is called arcsine. | + | Another, analytical, approach starts with the function $\phi$ defined on the closed interval $[-1,1]$ by $\phi(x)=\int_0^xdt/\sqrt{1-t^2}$. For $x=\pm1$ this integral is improper, but convergent. It is easy to see that $\phi$ is monotone increasing and continuous on the closed interval $[-1,1]$ and differentiable on the open interval $(-1,1)$, and has values in $[-\pi/2,\pi/2]$. So it has an inverse function, defined on $[-\pi/2,\pi/2]$, with values in $[-1,1]$. This function is called $\sin x$, and it can be proved that the domain of definition of this function can be continued to the whole real axis. The function $\phi$ is called arcsine. |
| | | | |
| − | The graph of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085480/s08548042.png" /> is the [[Sinusoid|sinusoid]] (see also [[Trigonometric functions|Trigonometric functions]]). | + | The graph of $\sin x$ is the [[Sinusoid|sinusoid]] (see also [[Trigonometric functions|Trigonometric functions]]). |
| | | | |
| | ====References==== | | ====References==== |
| | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972) pp. §4.3</TD></TR></table> | | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972) pp. §4.3</TD></TR></table> |
One of the trigonometric functions:
$$y=\sin x.$$
The domain of definition is the whole real line and the range of values is the interval $[-1,1]$. The sine is an odd periodic function of period $2\pi$. Sine and cosine are connected by the formula
$$\sin^2x+\cos^2x=1.$$
Sine and cosecant are connected by the formula
$$\sin x=\frac{1}{\operatorname{cosec}x}.$$
The derivative of sine is:
$$(\sin x)'=\cos x.$$
The indefinite integral of sine is:
$$\int\sin xdx=-\cos x+C.$$
Sine has the following power series representation:
$$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\ldots,\quad-\infty<x<\infty.$$
The function inverse to sine is called arcsine.
The sine and cosine of a complex argument $z$ are related to the exponential function by Euler's formulas:
$$e^{iz}=\cos z+i\sin z,\\\sin z=\frac{e^{iz}-e^{-iz}}{2i},$$
and if $z=ix$ is pure imaginary, then
$$\sin ix=-\sinh x,$$
where $\sinh x$ is the hyperbolic sine.
Of course, $\sin x$ can be defined by the Euler formulas or by its power series. A visual definition runs as follows. Consider the unit circle with centre at the origin $O$ in a rectangular coordinate system and with a rotating radius vector $OP$. Let $x$ be the angle between $OA$ and $OP$ (being reckoned positive in the counter-clockwise direction) and let $P'$ be the projection of $P$ on $OA$. Then $\sin x$ is defined as the ratio $(PP')/(OP)$, $\cos x$ as the ratio $(OP')/(OP)$ and $\tan x$ as the ratio $(PP')/(OP')$.
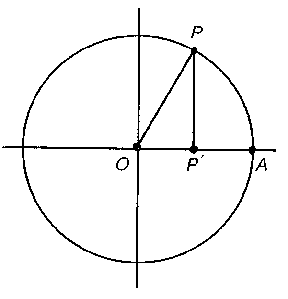
Figure: s085480a
Another, analytical, approach starts with the function $\phi$ defined on the closed interval $[-1,1]$ by $\phi(x)=\int_0^xdt/\sqrt{1-t^2}$. For $x=\pm1$ this integral is improper, but convergent. It is easy to see that $\phi$ is monotone increasing and continuous on the closed interval $[-1,1]$ and differentiable on the open interval $(-1,1)$, and has values in $[-\pi/2,\pi/2]$. So it has an inverse function, defined on $[-\pi/2,\pi/2]$, with values in $[-1,1]$. This function is called $\sin x$, and it can be proved that the domain of definition of this function can be continued to the whole real axis. The function $\phi$ is called arcsine.
The graph of $\sin x$ is the sinusoid (see also Trigonometric functions).
References
| [a1] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972) pp. §4.3 |
