Semi-simple algebraic group

A connected linear algebraic group of positive dimension which contains only trivial solvable (or, equivalently, Abelian) connected closed normal subgroups. The quotient group of a connected non-solvable linear group by its radical is semi-simple.

A connected linear algebraic group 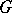of positive dimension is called simple (or quasi-simple) if it does not contain proper connected closed normal subgroups. The centre 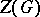of a simple group 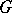is finite, and 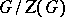is simple as an abstract group. An algebraic group 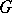is semi-simple if and only if 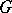is a product of simple connected closed normal subgroups.

If the ground field is the field 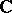of complex numbers, a semi-simple algebraic group is nothing but a semi-simple Lie group over 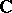(cf. Lie group, semi-simple). It turns out that the classification of semi-simple algebraic groups over an arbitrary algebraically closed field 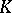is analogous to the case 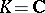, that is, a semi-simple algebraic group is determined up to isomorphism by its root system and a certain sublattice in the weight lattice that contains all the roots. More precisely, let 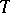be a maximal torus in the semi-simple algebraic group 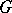and let 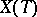be the character group of 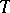, regarded as a lattice in the space 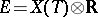. 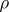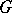For a rational linear representation of , the group 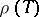is diagonalizable. Its eigenvalues, which are elements of 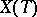, are called the weights of the representation 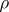. The non-zero weights of the adjoint representation 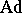are called the roots of 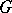. It turns out that the system 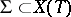of all roots of 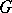is a root system in the space 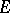, and that the irreducible components of the system 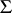are the root systems for the simple closed normal subgroups of 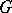. Furthermore, 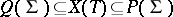, where is the lattice spanned by all roots and 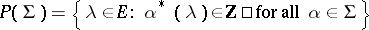is the weight lattice in the root system 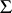. In the case 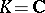the space 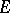can be naturally identified with a real subspace 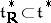, where 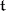is the Lie algebra of the torus 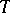, spanned by the differentials of all characters, while the lattices in 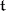dual to 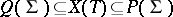coincide (up to a factor 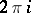) with 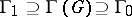(see Lie group, semi-simple).

The main classification theorem states that if 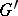is another semi-simple algebraic group, 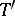its maximal torus, 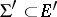a root system of 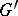, and if there is a linear mapping 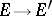giving an isomorphism between the root systems 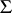and 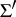and mapping 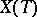onto 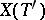, then 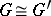(local isomorphism). Moreover, for any reduced root system 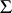and any lattice 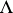satisfying the condition 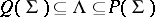there exists a semi-simple algebraic group 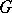such that 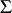is its root system with respect to the maximal torus 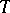, and .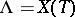

The isogenies (in particular, all automorphisms, cf. Isogeny) of a semi-simple algebraic group have also been classified.

References

[1]	R.G. Steinberg, "Lectures on Chevalley groups" , Yale Univ. Press (1968)
[2]	J.E. Humphreys, "Linear algebraic groups" , Springer (1975)

References

[a1]	T.A. Springer, "Linear algebraic groups" , Birkhäuser (1981)