Schubert variety
The set of all 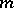 -dimensional subspaces
-dimensional subspaces 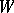 of an
of an  -dimensional vector space
-dimensional vector space  over a field
over a field  satisfying the Schubert conditions:
satisfying the Schubert conditions: 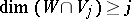 ,
, 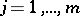 , where
, where 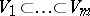 is a fixed flag of subspaces of
is a fixed flag of subspaces of 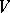 . In Grassmann coordinates these conditions are given by linear equations; a Schubert variety is an irreducible (generally speaking, singular) algebraic subvariety of the Grassmann manifold
. In Grassmann coordinates these conditions are given by linear equations; a Schubert variety is an irreducible (generally speaking, singular) algebraic subvariety of the Grassmann manifold 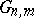 . Schubert varieties define a basis of the Chow ring
. Schubert varieties define a basis of the Chow ring 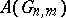 , and for
, and for 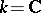 — a basis for the homology group
— a basis for the homology group 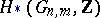 .
.
The Schubert conditions were considered by H. Schubert in connection with enumeration problems for geometric objects with given incidence properties. Hilbert's 15th problem concerns a foundation for the enumeration theory developed by Schubert (see [2]).
References
| [1] | H. Schubert, "Lösung des Charakteristiken-Problems für lineare Räume beliebiger Dimension" Mitt. Math. Gesellschaft Hamburg , 1 (1889) pp. 134–155 Zbl 18.0631.01 |
| [2] | S.L. Kleiman, "Problem 15. Rigorous foundation of Schubert's enumerative calculus" F.E. Browder (ed.) , Mathematical developments arising from Hilbert problems , Proc. Symp. Pure Math. , 28 , Amer. Math. Soc. (1976) pp. 445–482 MR0429938 |
| [3] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , 1 , Wiley (Interscience) (1978) MR0507725 Zbl 0408.14001 |
| [4] | W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , 2 , Cambridge Univ. Press (1954) MR0061846 Zbl 0055.38705 |
Comments
The notion of a Schubert variety has been generalized to any complete homogeneous space of a semi-simple linear algebraic group 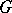 . It is the Zariski closure of any Bruhat cell ([a1]). The geometry of Schubert varieties was studied, e.g., in [a2], [a3].
. It is the Zariski closure of any Bruhat cell ([a1]). The geometry of Schubert varieties was studied, e.g., in [a2], [a3].
References
| [a1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) pp. 283ff MR0251042 Zbl 0206.49801 Zbl 0186.33201 |
| [a2] | M. Demazure, "Désingularisation des variétés de Schubert généralisés" Ann. Sci. Ecole Norm. Sup. , 7 (1974) pp. 53–87 |
| [a3] | V. Laksnibai, C. Seshadri, "Geometry of 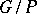 - V" J. of Algebra , 100 (1986) pp. 462–557 MR840589 - V" J. of Algebra , 100 (1986) pp. 462–557 MR840589 |
Schubert variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schubert_variety&oldid=12151