Sahlqvist theorem
A theorem about the relational properties expressed by formulas of modal logic, and about canonicity of modal formulas.
To be precise, let a positive (negative) formula of modal logic be one where all proposition letters occur in the scope of an even (odd) number of negation signs only. Let a Sahlqvist antecedent be a formula that is built up from proposition letters prefixed by any finite number of necessity operators  and negative formulas, using only
and negative formulas, using only 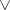 ,
, 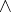 and the possibility operator
and the possibility operator  . Then, a Sahlqvist formula is any formula that may be obtained by applying conjunctions and necessity operators
. Then, a Sahlqvist formula is any formula that may be obtained by applying conjunctions and necessity operators  to implications of the form
to implications of the form 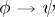 , where
, where 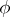 is a Sahlqvist antecedent and
is a Sahlqvist antecedent and 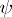 is a positive formula. For example,
is a positive formula. For example, 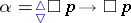 is a Sahlqvist formula.
is a Sahlqvist formula.
Sahlqvist's theorem states two things. First, although, in general, every modal formula is equivalent to a second-order formula, Sahlqvist formulas have a first-order equivalent (cf. Modal logic); moreover, this first-order equivalent  of
of 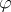 may be obtained in an effective way. For instance, for
may be obtained in an effective way. For instance, for 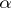 as above,
as above, 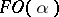 expresses Euclidicity:
expresses Euclidicity: 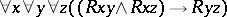 . Secondly, every Sahlqvist formula is canonical. Here, canonicity of a modal formula means that it is valid on the canonical frame. Algebraically, the latter may be viewed as the Stone representation of the free Boolean algebra with operators over
. Secondly, every Sahlqvist formula is canonical. Here, canonicity of a modal formula means that it is valid on the canonical frame. Algebraically, the latter may be viewed as the Stone representation of the free Boolean algebra with operators over 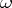 many generators. Canonicity of a modal formula
many generators. Canonicity of a modal formula 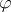 implies that the modal logic obtained from the minimal logic
implies that the modal logic obtained from the minimal logic 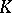 by adding
by adding 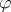 as an axiom, is axiomatically complete with respect to the class of models satisfying
as an axiom, is axiomatically complete with respect to the class of models satisfying 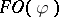 . Thus, the modal logic
. Thus, the modal logic  is complete with respect to Euclidean Kripke frames (cf. also Kripke models).
is complete with respect to Euclidean Kripke frames (cf. also Kripke models).
References
| [a1] | J. van Benthem, "Correspondence theory" D. Gabbay (ed.) F. Guenthner (ed.) , Handbook of Philos. Logic , 2 , Reidel (1984) pp. 167–242 |
| [a2] | M. Kracht, "How completeness and correspondence got married" M. de Rijke (ed.) , Diamonds and Defaults , Kluwer Acad. Publ. (1993) pp. 175–214 |
| [a3] | H. Sahlqvist, "Completeness and correspondence in the first and second order semantics for modal logic" S. Kanger (ed.) , Proc. Third Scand. Logic Symp. Uppsala (1973) , North-Holland (1975) pp. 110–143 |
| [a4] | G. Sambin, V. Vaccaro, "A new proof of Sahlqvist's theorem on modal definability and completeness" J. Symb. Logic , 54 (1989) pp. 992–999 |
Sahlqvist theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sahlqvist_theorem&oldid=17405