Difference between revisions of "S-duality"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex done, typos) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | s0830002.png | ||
| + | $#A+1 = 101 n = 2 | ||
| + | $#C+1 = 101 : ~/encyclopedia/old_files/data/S083/S.0803000 \BMI S\EMI\AAhduality, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''stationary duality, Spanier duality'' | ''stationary duality, Spanier duality'' | ||
| − | A [[Duality|duality]] in homotopy theory which exists (in the absence of restrictions imposed on the dimensions of spaces) for the analogues of ordinary homotopy and cohomotopy groups in the suspension category — for the | + | A [[Duality|duality]] in homotopy theory which exists (in the absence of restrictions imposed on the dimensions of spaces) for the analogues of ordinary homotopy and cohomotopy groups in the suspension category — for the $ S $- |
| + | homotopy and $ S $- | ||
| + | cohomotopy groups or stationary homotopy and cohomotopy groups, forming extra-ordinary (generalized) homology and cohomology theories. A suspension category, or $ S $- | ||
| + | category, is a [[Category|category]] whose objects are topological spaces $ X $, | ||
| + | while its morphisms are classes $ \{ f \} $ | ||
| + | of $ S $- | ||
| + | homotopic mappings $ f $ | ||
| + | from a $ p $- | ||
| + | fold [[Suspension|suspension]] $ S ^ { p } X _ { 1 } $ | ||
| + | into $ S ^ { p } X _ { 2 } $, | ||
| + | $ f $ | ||
| + | and $ g: S ^ { q } X _ { 1 } \rightarrow S ^ { q } X _ { 2 } $ | ||
| + | being considered as $ S $- | ||
| + | homotopic if there exists an $ r \geq \max { ( p, q) } $ | ||
| + | such that the suspensions $ S ^ { {r-p} } f $ | ||
| + | and $ S ^ { {r-q} } g $ | ||
| + | are homotopic in the ordinary sense. The set $ \{ X _ { 1 } , X _ { 2 } \} $ | ||
| + | of such classes, which are known as $ S $- | ||
| + | mappings, constitutes an Abelian group with respect to the so-called track addition [[#References|[1]]], [[#References|[2]]], [[#References|[4]]], [[#References|[5]]]. The group $ \{ X _ { 1 } , X _ { 2 } \} $ | ||
| + | is the limit of the direct spectrum of the sets $ [ S ^ { k } X _ { 1 } , S ^ { k } X _ { 2 } ] $ | ||
| + | of ordinary homotopy classes with suspension mappings as projections; if $ k $ | ||
| + | is sufficiently large, it is a group spectrum with homomorphisms. There exists an isomorphism $ S: \{ X _ { 1 } , X _ { 2 } \} \rightarrow \{ SX _ { 1 } , SX _ { 2 } \} $ | ||
| + | in which the corresponding elements are represented by one and the same mapping $ S ^ { p } X _ { 1 } \rightarrow S ^ { p } X _ { 2 } $, | ||
| + | $ p \geq 1 $. | ||
| + | The $ n $- | ||
| + | dual polyhedron of the polyhedron $ X $ | ||
| + | in a sphere $ S ^ { n } $ | ||
| + | is an arbitrary polyhedron $ D _ { n } X $ | ||
| + | in $ S ^ { n } $ | ||
| + | which is an $ S $- | ||
| + | deformation retract of the complement $ S ^ { n } \setminus X $, | ||
| + | i.e. the morphism corresponding to the imbedding $ D _ { n } X \subset S ^ { n } \setminus X $ | ||
| + | is an $ S $- | ||
| + | equivalence. The polyhedron $ D _ { n } X $ | ||
| + | exists for all $ X $, | ||
| + | and $ X $ | ||
| + | may be considered as $ D _ { n } ^ { 2 } X $. | ||
| − | For any polyhedra | + | For any polyhedra $ X _ { 1 } , X _ { 2 } $ |
| + | and any polyhedra $ D _ { n } X _ { 1 } $ | ||
| + | and $ D _ { n } X _ { 2 } $ | ||
| + | which are dual to them, there exists a unique mapping | ||
| − | + | $$ | |
| + | D _ { n } : \{ X _ { 1 } , X _ { 2 } \} \rightarrow \ | ||
| + | \{ D _ { n } X _ { 2 } , D _ { n } X _ { 1 } \} | ||
| + | $$ | ||
satisfying the following conditions: | satisfying the following conditions: | ||
| − | a) It is an involutory contravariant functorial isomorphism, i.e. | + | a) It is an involutory contravariant functorial isomorphism, i.e. $ D _ { n } $ |
| + | is a homomorphism such that if | ||
| − | + | $$ | |
| + | i : X _ { 1 } \subset X _ { 2 } \ \textrm{ and } \ i ^ \prime : D _ { n } X _ { 2 } | ||
| + | \subset D _ { n } X _ { 1 } , | ||
| + | $$ | ||
then | then | ||
| − | + | $$ | |
| + | D _ { n } \{ i \} = \{ i ^ \prime \} ; | ||
| + | $$ | ||
if | if | ||
| − | + | $$ | |
| + | \{ f _ { 1 } \} \in \{ X _ { 1 } , X _ { 2 } \} \ \textrm{ and } \ \ | ||
| + | \{ f _ { 2 } \} \in \{ X _ { 2 } , X _ { 3 } \} , | ||
| + | $$ | ||
then | then | ||
| − | + | $$ | |
| + | D _ { n } { ( \{ f _ { 2 } \} \cdot \{ f _ { 1 } \} ) } = \ | ||
| + | D _ { n } \{ f _ { 1 } \} \cdot D _ { n } \{ f _ { 2 } \} ; | ||
| + | $$ | ||
| − | if | + | if $ \theta $ |
| + | is an element of $ \{ X _ { 1 } , X _ { 2 } \} $ | ||
| + | or of $ \{ D _ { n } X _ { 2 } , D _ { n } X _ { 1 } \} $, | ||
| + | then $ D _ { n } D _ { n } \theta = \theta $. | ||
b) The following relations are valid: | b) The following relations are valid: | ||
| − | + | $$ | |
| + | SD _ { n } = D _ { {n+1} } \ \textrm{ and } \ D _ { {n+1} } S = D _ { n } , | ||
| + | $$ | ||
| − | where | + | where $ SD _ { n } X _ { i } $ |
| + | and $ D _ { n } X _ { i } $ | ||
| + | are considered as polyhedra, $ { ( {n+1} ) } $- | ||
| + | dual to polyhedra $ X _ { i } $ | ||
| + | and, correspondingly, $ SX _ { i } $, | ||
| + | $ i = 1, 2; $ | ||
| + | this means that it does not depend on $ n $ | ||
| + | and is stationary with respect to suspension. | ||
c) It satisfies the equation | c) It satisfies the equation | ||
| − | + | $$ | |
| + | D _ { a } ^ { n } \theta _ { * } = { ( D _ { n } \theta ) } ^ { * } D _ { a } ^ { n } , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | \theta _ { * } : H _ { p } { ( X _ { 1 } ) } \rightarrow H _ { p } { ( X _ { 2 } ) } | ||
| + | $$ | ||
and | and | ||
| − | + | $$ | |
| + | { ( D _ { n } \theta ) } ^ { * } : H ^ { { {n-p} -1} } | ||
| + | { ( D _ { n } X _ { 1 } ) } \rightarrow H ^ { { {n-p} -1} } { ( D _ { n } X _ { 2 } ) } | ||
| + | $$ | ||
| − | are homomorphisms of the above homology and cohomology groups, induced by | + | are homomorphisms of the above homology and cohomology groups, induced by $ S $- |
| + | mappings $ \theta \in \{ X _ { 1 } , X _ { 2 } \} $ | ||
| + | and $ D _ { n } \theta $, | ||
| + | and | ||
| − | + | $$ | |
| + | D _ { a } : H _ { p } { ( X _ { i } ) } \rightarrow H ^ { { {n-p} -1} } | ||
| + | { ( D _ { n } X _ { i } ) } ,\ {i=1} , 2 , | ||
| + | $$ | ||
| − | is an isomorphism obtained from the isomorphism of [[Alexander duality|Alexander duality]] by replacing the set | + | is an isomorphism obtained from the isomorphism of [[Alexander duality|Alexander duality]] by replacing the set $ S ^ { n } \setminus X _ { i } $ |
| + | by its $ S $- | ||
| + | deformation retract $ D _ { n } X _ { i } $. | ||
| − | The construction of | + | The construction of $ D _ { n } $ |
| + | is based on the representation of a given mapping as the composition of an imbedding and an $ S $- | ||
| + | deformation retract. | ||
| − | The | + | The $ S $- |
| + | homotopy group $ \Sigma _ { p } { ( X) } $ | ||
| + | of a space $ X $ | ||
| + | is the group $ \{ S ^ { p } , X \} $, | ||
| + | and the $ S $- | ||
| + | cohomotopy group $ \Sigma ^ { p } { ( X) } $ | ||
| + | of $ X $ | ||
| + | is the group $ \{ X, S ^ { p } \} $. | ||
| + | As in ordinary homotopy theory, one defines the homomorphisms | ||
| − | + | $$ | |
| + | \phi _ { p } : \Sigma _ { p } { ( X) } \rightarrow H _ { p } { ( X) } , | ||
| + | $$ | ||
| − | + | $$ | |
| + | \phi ^ { p } : \Sigma ^ { p } { ( X) } \rightarrow H ^ { p } { ( X) } . | ||
| + | $$ | ||
| − | Regarding the spheres | + | Regarding the spheres $ S ^ { p } $ |
| + | and $ S ^ { { {n-p} -1} } $ | ||
| + | as $ n $- | ||
| + | dual leads to the isomorphisms | ||
| − | + | $$ | |
| + | D _ { n } : \Sigma _ { p } { ( X) } \rightarrow \Sigma ^ { { {n-p} -1} } { ( D _ { n } X) } | ||
| + | $$ | ||
and to the commutative diagram | and to the commutative diagram | ||
| − | + | $$ | |
| + | |||
| + | \begin{array}{ccc} | ||
| + | {\Sigma _ { p } { ( X) } } & \stackrel{ \phi _ p }{\rightarrow} &{H _ { p } { ( X) } } \\ | ||
| + | { { {D _ { n } } } \downarrow } &{} &{\downarrow { {D _ { a } ^ { n } } } } \\ | ||
| + | {\Sigma ^ { { {n-p} -1} } { ( D _ { n } ^ { X } ) } } & \stackrel{\phi ^{n-p-1}}{\rightarrow} &{H ^ { { {n-p} -1} } { ( D _ { n } X) } } \\ | ||
| + | \end{array} | ||
| + | |||
| + | $$ | ||
| − | Thus, the isomorphism | + | Thus, the isomorphism $ D _ { n } $ |
| + | connects $ S $- | ||
| + | homotopy and $ S $- | ||
| + | cohomotopy groups, just as the isomorphism of Alexander duality $ D _ { a } ^ { n } $ | ||
| + | connects the homology and cohomology groups. Any duality in the $ S $- | ||
| + | category entails a duality of ordinary homotopy classes if the conditions imposed on the space entail the existence of a one-to-one correspondence between the set of the above classes and the set of $ S $- | ||
| + | homotopy classes. | ||
| − | Examples of dual assumptions in this theory include Hurewicz's isomorphism theorem and Hopf's classification theorem. | + | Examples of dual assumptions in this theory include Hurewicz's isomorphism theorem and Hopf's classification theorem. $ D _ { n } $ |
| + | converts one of these theorems into the other, which means that $ S $- | ||
| + | homotopy groups are replaced by $ S $- | ||
| + | cohomotopy groups, homology groups by cohomology groups, the mapping $ \phi _ { p } $ | ||
| + | by the mapping $ \phi ^ { { {n-p} -1} } $, | ||
| + | the smallest dimension with a non-trivial homology group by the largest dimension with a non-trivial cohomology group, and vice versa. In ordinary homotopy theory the definition of an $ n $- | ||
| + | cohomotopy group requires that the dimension of the space does not exceed $ {2n-2} $( | ||
| + | or, more generally, that the space be $ { { ( 2n-1) }} $- | ||
| + | coconnected, $ n > 1 $), | ||
| + | which impairs the perfectly general nature of duality. | ||
| − | There are several trends of generalization of the theory: e.g. studies are made of spaces with the | + | There are several trends of generalization of the theory: e.g. studies are made of spaces with the $ S $- |
| + | homotopy type of polyhedra, the relative case, a theory with supports, etc. [[#References|[3]]], [[#References|[5]]], , [[#References|[7]]]. The theory was one of the starting points in the development of stationary homotopy theory [[#References|[8]]]. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E.H. Spanier, "Duality and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s083000109.png" />-theory" ''Bull. Amer. Math. Soc.'' , '''62''' (1956) pp. 194–203 {{MR|0085506}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E.H. Spanier, J.H.C. Whitehead, "Duality in homotopy theory" ''Mathematika'' , '''2''' : 3 (1955) pp. 56–80 {{MR|0074823}} {{ZBL|0064.17202}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.H. Spanier, J.H.C. Whitehead, "Duality in relative homotopy theory" ''Ann. of Math.'' , '''67''' : 2 (1958) pp. 203–238 {{MR|0105105}} {{ZBL|0092.15701}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.G. Barratt, "Track groups 1; 2" ''Proc. London Math. Soc.'' , '''5''' (1955) pp. 71–106; 285–329</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E.H. Spanier, J.H.C. Whitehead, "The theory of carriers and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083000/s083000110.png" />-theory" , ''Algebraic geometry and Topology (A Symp. in honor of S. Lefschetz)'' , Princeton Univ. Press (1957) pp. 330–360 {{MR|0084772}} {{ZBL|}} </TD></TR><TR><TD valign="top">[6a]</TD> <TD valign="top"> B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Groupes absolus" ''C.R. Acad. Sci. Paris'' , '''246''' : 17 (1958) pp. 2444–2447 {{MR|0100261}} {{ZBL|0092.39901}} </TD></TR><TR><TD valign="top">[6b]</TD> <TD valign="top"> B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Suites exactes" ''C.R. Acad. Sci. Paris'' , '''246''' : 18 (1958) pp. 2555–2558 {{MR|0100262}} {{ZBL|0092.40001}} </TD></TR><TR><TD valign="top">[6c]</TD> <TD valign="top"> B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Coefficients" ''C.R. Acad. Sci. Paris'' , '''246''' : 21 (1958) pp. 2991–2993 {{MR|0100263}} {{ZBL|0092.40101}} </TD></TR><TR><TD valign="top">[6d]</TD> <TD valign="top"> B. Eckmann, P.J. Hilton, "Transgression homotopique et cohomologique" ''C.R. Acad. Sci. Paris'' , '''247''' : 6 (1958) pp. 620–623 {{MR|0100264}} {{ZBL|0092.40102}} </TD></TR><TR><TD valign="top">[6e]</TD> <TD valign="top"> B. Eckmann, P.J. Hilton, "Décomposition homologique d'un polyhèdre simplement connexe" ''C.R. Acad. Sci. Paris'' , '''248''' : 14 (1959) pp. 2054–2056</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) {{MR|0210112}} {{MR|1325242}} {{ZBL|0145.43303}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> G.W. Whitehead, "Recent advances in homotopy theory" , Amer. Math. Soc. (1970) {{MR|0309097}} {{ZBL|0217.48601}} </TD></TR></table> |
Latest revision as of 13:45, 8 June 2020
stationary duality, Spanier duality
A duality in homotopy theory which exists (in the absence of restrictions imposed on the dimensions of spaces) for the analogues of ordinary homotopy and cohomotopy groups in the suspension category — for the $ S $- homotopy and $ S $- cohomotopy groups or stationary homotopy and cohomotopy groups, forming extra-ordinary (generalized) homology and cohomology theories. A suspension category, or $ S $- category, is a category whose objects are topological spaces $ X $, while its morphisms are classes $ \{ f \} $ of $ S $- homotopic mappings $ f $ from a $ p $- fold suspension $ S ^ { p } X _ { 1 } $ into $ S ^ { p } X _ { 2 } $, $ f $ and $ g: S ^ { q } X _ { 1 } \rightarrow S ^ { q } X _ { 2 } $ being considered as $ S $- homotopic if there exists an $ r \geq \max { ( p, q) } $ such that the suspensions $ S ^ { {r-p} } f $ and $ S ^ { {r-q} } g $ are homotopic in the ordinary sense. The set $ \{ X _ { 1 } , X _ { 2 } \} $ of such classes, which are known as $ S $- mappings, constitutes an Abelian group with respect to the so-called track addition [1], [2], [4], [5]. The group $ \{ X _ { 1 } , X _ { 2 } \} $ is the limit of the direct spectrum of the sets $ [ S ^ { k } X _ { 1 } , S ^ { k } X _ { 2 } ] $ of ordinary homotopy classes with suspension mappings as projections; if $ k $ is sufficiently large, it is a group spectrum with homomorphisms. There exists an isomorphism $ S: \{ X _ { 1 } , X _ { 2 } \} \rightarrow \{ SX _ { 1 } , SX _ { 2 } \} $ in which the corresponding elements are represented by one and the same mapping $ S ^ { p } X _ { 1 } \rightarrow S ^ { p } X _ { 2 } $, $ p \geq 1 $. The $ n $- dual polyhedron of the polyhedron $ X $ in a sphere $ S ^ { n } $ is an arbitrary polyhedron $ D _ { n } X $ in $ S ^ { n } $ which is an $ S $- deformation retract of the complement $ S ^ { n } \setminus X $, i.e. the morphism corresponding to the imbedding $ D _ { n } X \subset S ^ { n } \setminus X $ is an $ S $- equivalence. The polyhedron $ D _ { n } X $ exists for all $ X $, and $ X $ may be considered as $ D _ { n } ^ { 2 } X $.
For any polyhedra $ X _ { 1 } , X _ { 2 } $ and any polyhedra $ D _ { n } X _ { 1 } $ and $ D _ { n } X _ { 2 } $ which are dual to them, there exists a unique mapping
$$ D _ { n } : \{ X _ { 1 } , X _ { 2 } \} \rightarrow \ \{ D _ { n } X _ { 2 } , D _ { n } X _ { 1 } \} $$
satisfying the following conditions:
a) It is an involutory contravariant functorial isomorphism, i.e. $ D _ { n } $ is a homomorphism such that if
$$ i : X _ { 1 } \subset X _ { 2 } \ \textrm{ and } \ i ^ \prime : D _ { n } X _ { 2 } \subset D _ { n } X _ { 1 } , $$
then
$$ D _ { n } \{ i \} = \{ i ^ \prime \} ; $$
if
$$ \{ f _ { 1 } \} \in \{ X _ { 1 } , X _ { 2 } \} \ \textrm{ and } \ \ \{ f _ { 2 } \} \in \{ X _ { 2 } , X _ { 3 } \} , $$
then
$$ D _ { n } { ( \{ f _ { 2 } \} \cdot \{ f _ { 1 } \} ) } = \ D _ { n } \{ f _ { 1 } \} \cdot D _ { n } \{ f _ { 2 } \} ; $$
if $ \theta $ is an element of $ \{ X _ { 1 } , X _ { 2 } \} $ or of $ \{ D _ { n } X _ { 2 } , D _ { n } X _ { 1 } \} $, then $ D _ { n } D _ { n } \theta = \theta $.
b) The following relations are valid:
$$ SD _ { n } = D _ { {n+1} } \ \textrm{ and } \ D _ { {n+1} } S = D _ { n } , $$
where $ SD _ { n } X _ { i } $ and $ D _ { n } X _ { i } $ are considered as polyhedra, $ { ( {n+1} ) } $- dual to polyhedra $ X _ { i } $ and, correspondingly, $ SX _ { i } $, $ i = 1, 2; $ this means that it does not depend on $ n $ and is stationary with respect to suspension.
c) It satisfies the equation
$$ D _ { a } ^ { n } \theta _ { * } = { ( D _ { n } \theta ) } ^ { * } D _ { a } ^ { n } , $$
where
$$ \theta _ { * } : H _ { p } { ( X _ { 1 } ) } \rightarrow H _ { p } { ( X _ { 2 } ) } $$
and
$$ { ( D _ { n } \theta ) } ^ { * } : H ^ { { {n-p} -1} } { ( D _ { n } X _ { 1 } ) } \rightarrow H ^ { { {n-p} -1} } { ( D _ { n } X _ { 2 } ) } $$
are homomorphisms of the above homology and cohomology groups, induced by $ S $- mappings $ \theta \in \{ X _ { 1 } , X _ { 2 } \} $ and $ D _ { n } \theta $, and
$$ D _ { a } : H _ { p } { ( X _ { i } ) } \rightarrow H ^ { { {n-p} -1} } { ( D _ { n } X _ { i } ) } ,\ {i=1} , 2 , $$
is an isomorphism obtained from the isomorphism of Alexander duality by replacing the set $ S ^ { n } \setminus X _ { i } $ by its $ S $- deformation retract $ D _ { n } X _ { i } $.
The construction of $ D _ { n } $ is based on the representation of a given mapping as the composition of an imbedding and an $ S $- deformation retract.
The $ S $- homotopy group $ \Sigma _ { p } { ( X) } $ of a space $ X $ is the group $ \{ S ^ { p } , X \} $, and the $ S $- cohomotopy group $ \Sigma ^ { p } { ( X) } $ of $ X $ is the group $ \{ X, S ^ { p } \} $. As in ordinary homotopy theory, one defines the homomorphisms
$$ \phi _ { p } : \Sigma _ { p } { ( X) } \rightarrow H _ { p } { ( X) } , $$
$$ \phi ^ { p } : \Sigma ^ { p } { ( X) } \rightarrow H ^ { p } { ( X) } . $$
Regarding the spheres $ S ^ { p } $ and $ S ^ { { {n-p} -1} } $ as $ n $- dual leads to the isomorphisms
$$ D _ { n } : \Sigma _ { p } { ( X) } \rightarrow \Sigma ^ { { {n-p} -1} } { ( D _ { n } X) } $$
and to the commutative diagram
$$ \begin{array}{ccc} {\Sigma _ { p } { ( X) } } & \stackrel{ \phi _ p }{\rightarrow} &{H _ { p } { ( X) } } \\ { { {D _ { n } } } \downarrow } &{} &{\downarrow { {D _ { a } ^ { n } } } } \\ {\Sigma ^ { { {n-p} -1} } { ( D _ { n } ^ { X } ) } } & \stackrel{\phi ^{n-p-1}}{\rightarrow} &{H ^ { { {n-p} -1} } { ( D _ { n } X) } } \\ \end{array} $$
Thus, the isomorphism $ D _ { n } $ connects $ S $- homotopy and $ S $- cohomotopy groups, just as the isomorphism of Alexander duality $ D _ { a } ^ { n } $ connects the homology and cohomology groups. Any duality in the $ S $- category entails a duality of ordinary homotopy classes if the conditions imposed on the space entail the existence of a one-to-one correspondence between the set of the above classes and the set of $ S $- homotopy classes.
Examples of dual assumptions in this theory include Hurewicz's isomorphism theorem and Hopf's classification theorem. $ D _ { n } $ converts one of these theorems into the other, which means that $ S $- homotopy groups are replaced by $ S $- cohomotopy groups, homology groups by cohomology groups, the mapping $ \phi _ { p } $ by the mapping $ \phi ^ { { {n-p} -1} } $, the smallest dimension with a non-trivial homology group by the largest dimension with a non-trivial cohomology group, and vice versa. In ordinary homotopy theory the definition of an $ n $- cohomotopy group requires that the dimension of the space does not exceed $ {2n-2} $( or, more generally, that the space be $ { { ( 2n-1) }} $- coconnected, $ n > 1 $), which impairs the perfectly general nature of duality.
There are several trends of generalization of the theory: e.g. studies are made of spaces with the $ S $- homotopy type of polyhedra, the relative case, a theory with supports, etc. [3], [5], , [7]. The theory was one of the starting points in the development of stationary homotopy theory [8].
References
| [1] | E.H. Spanier, "Duality and 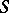 -theory" Bull. Amer. Math. Soc. , 62 (1956) pp. 194–203 MR0085506 -theory" Bull. Amer. Math. Soc. , 62 (1956) pp. 194–203 MR0085506 |
| [2] | E.H. Spanier, J.H.C. Whitehead, "Duality in homotopy theory" Mathematika , 2 : 3 (1955) pp. 56–80 MR0074823 Zbl 0064.17202 |
| [3] | E.H. Spanier, J.H.C. Whitehead, "Duality in relative homotopy theory" Ann. of Math. , 67 : 2 (1958) pp. 203–238 MR0105105 Zbl 0092.15701 |
| [4] | M.G. Barratt, "Track groups 1; 2" Proc. London Math. Soc. , 5 (1955) pp. 71–106; 285–329 |
| [5] | E.H. Spanier, J.H.C. Whitehead, "The theory of carriers and 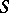 -theory" , Algebraic geometry and Topology (A Symp. in honor of S. Lefschetz) , Princeton Univ. Press (1957) pp. 330–360 MR0084772 -theory" , Algebraic geometry and Topology (A Symp. in honor of S. Lefschetz) , Princeton Univ. Press (1957) pp. 330–360 MR0084772 |
| [6a] | B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Groupes absolus" C.R. Acad. Sci. Paris , 246 : 17 (1958) pp. 2444–2447 MR0100261 Zbl 0092.39901 |
| [6b] | B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Suites exactes" C.R. Acad. Sci. Paris , 246 : 18 (1958) pp. 2555–2558 MR0100262 Zbl 0092.40001 |
| [6c] | B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Coefficients" C.R. Acad. Sci. Paris , 246 : 21 (1958) pp. 2991–2993 MR0100263 Zbl 0092.40101 |
| [6d] | B. Eckmann, P.J. Hilton, "Transgression homotopique et cohomologique" C.R. Acad. Sci. Paris , 247 : 6 (1958) pp. 620–623 MR0100264 Zbl 0092.40102 |
| [6e] | B. Eckmann, P.J. Hilton, "Décomposition homologique d'un polyhèdre simplement connexe" C.R. Acad. Sci. Paris , 248 : 14 (1959) pp. 2054–2056 |
| [7] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) MR0210112 MR1325242 Zbl 0145.43303 |
| [8] | G.W. Whitehead, "Recent advances in homotopy theory" , Amer. Math. Soc. (1970) MR0309097 Zbl 0217.48601 |
S-duality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=S-duality&oldid=17724